python pytorch教程-带你从入门到实战(代码全部可运行)
其实这个教程以前博主写过一次,不过,这回再写一次,打算内容写的多一点,由浅入深,然后加入一些实践案例。
下面是我们的内容目录:
1.先从数据类型谈起
1.1 如何生成pytorch的各种数据类型?
1.2 pytorch的各种数据类型有哪些属性?
1.3 pytorch的各种数据类型有哪些函数操作?
2.数据类型和其操作谈完,选择某一个方向开始学习和实践(深度学习)。
2.1 求导
2.2 损失函数
2.3优化器
2.4线性回归代码实战
2.5 卷积神经网络实战
2.6 神经网络实战
2.7 RNN和LSTM实战
1.先从数据类型谈起
那如果从数据类型谈起,我们就要从下面几个角度去谈:
1.1 如何生成pytorch的各种数据类型?
1.2 pytorch的各种数据类型有哪些属性?
1.3 pytorch的各种数据类型有哪些函数操作?
首先,我们知道pytorch是一个计算库,也有人说是深度学习库,那么计算库呢,肯定都是有自己的数据类型的。
另外pytorch都是围绕Tensors (张量)来进行计算的,Tensors 类似于 NumPy 的 ndarrays ,同时 Tensors 可以使用 GPU 进行计算。ndarrays 是不可以的,且只能存储在cpu中,但是Tensor可以,Tensor其实就是用来进行各种计算的数据结构,存储数据,且有各种各样的操作,增删改查之类的。
所以我们先从pytorch数据类型开始讲解,没有自己的数据类型,就无从谈起。当然其实大家如果学过数据结构就会知道,现在基本上想开发大型系统还是小型系统,还是说想开发一些功能接口,像pytorch其实就是一个功能接口,我们都需要从最基本的类开始设计,pytorch的每一个数据类型其实就是一个类,这个类会定义他的一些基本的数据,定义他的一些函数操作,比如乘法、加法、减法、乘法、梯度更新。所以,我们看待pytorch的数据类型的时候,可以从类的角度去看待它。
下面我们看一张图:
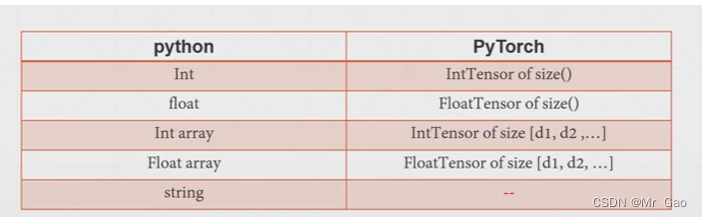
上图呢其实就是表示出了python的五个个数据类型和pytorch的五个数据类型的对应关系,其实pytorhc应该还有更多的,但是一般情况下掌握上面四种就可以了,即使你是做深度学习的,也只需要掌握上面四个。
下面我们开始正文:
1.1 如何生成pytorch的各种数据类型?
生成pytorch的各种数据类型比较简单,当然也分为甚多情况下面我们一一介绍:
在开始1.1之前,我们需要提前讲一个函数,这部分本来应该是在1.3来说的。
这个函数就是type
代码示例如下:
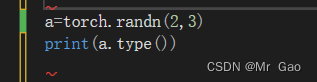
运行结果会返回他的变量的数据类型,这个函数我们在后面会常用到。

(1)通过pytorch的函数生成数据类型
1.randn函数,返回一个包含了从标准正态分布中抽取的一组随机数的张量
import torch
#使用torch函数生成torch数据类型
print(torch.randn(2,3))
print(torch.randn(2,3).type())
输入结果如下:
这个函数返回FloatTensor的张量。

2.rand函数,这个函数看似和randn函数很像但是其实是由很大区别的。
print(torch.rand(2,3))
print(torch.rand(2,3).type())
输出结果如下:
这个返回的也是FloatTensro数据类型的张量。

3.torch.eye(),返回一个二维张量,返回的也是FloatTensor数据类型的张量。学过线性代数的同学可能知道这个函数的作用是很大的哈。明星可以用来生成单位矩阵。
这里有个疑惑哈,都知道单位矩阵的元素其实一般都用整数表示,这里为什么也是float数据类型呢?所以说,pytorch就是为了计算方便,都整齐划一,都用FloatTensor张量的数据类型,这样不会出现类型转换数据流失,而且也方便操作。
print(torch.eye(2,3))
print(torch.eye(2,3).type())
4.from_numpy, 将numpy.ndarray转换为Tensor。
这个函数有很多限制嘛,比如返回的张量tensor和ndarray共享同一内存空间,修改一个会导致另一个也被修改,返回的张量不能改变大小。
所以用的时候要注意这些问题。
a=np.random.randn(2,3)
#print(a)
tor=torch.from_numpy(a)
print(tor)
print(tor.type())
输出结果如下,注意这是DoubleTensor的数据类型。

5.linspace ,返回一个一维张量,这个用法是说我们设置一个起点,一个终点,再设置一个间隔,就会按照设置的间隔从起点到终点返回数据。返回数据类型是FloatTensor。
注意,step只能是整数,start 和end可以随便设置
print(torch.linspace(2,10,2))
print(torch.linspace(2,10,2).type())
输出结果如下:
6.logspace,返回一个一维张量,设置一个起点,一个终点,还需要设置一个返回元素数量,会按等间隔返回区间内所需数量的元素。
对了这个函数还可以对数据进行按对数处理。
print(torch.logspace(2,10,20))
print(torch.logspace(2,10,20).type())
#以5为底对数据进行对数处理,默认为10
print(torch.logspace(2,10,20,5))
print(torch.logspace(2,10,20,5).type())
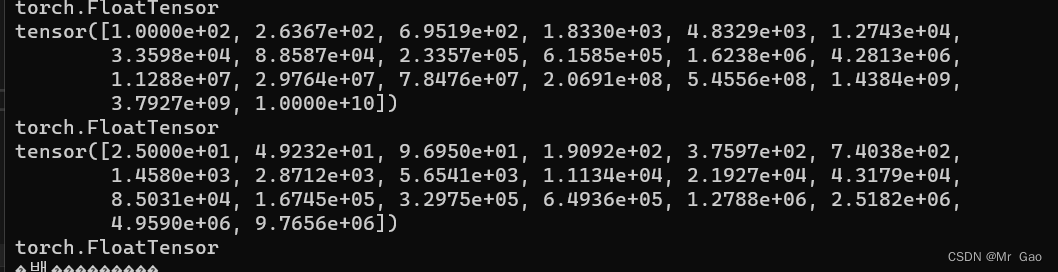 7.ones,返回一个全为1的张量
7.ones,返回一个全为1的张量
print(torch.ones(10))
print(torch.logspace(10))
返回数据类型也是FloatTensor。

8.randperm,返回一个随机的整数排列,所以只能传入整数n,然后排列的元素小于n。
print(torch.randperm(10))
print(torch.randperm(10).type())
注意这个返回类型是LongTensor。

9.arange函数,这个也是返回一个一维张量,他的用法跟logspace类似,但是他没有底数,底数一直是10.
下面看代码就懂了:
print(torch.arange(10))
print(torch.arange(2,10))
print(torch.arange(2,10,2))
print(torch.arange(2,10,0.5))
print(torch.arange(10).type())
print(torch.arange(2,10,0.5).type())
输出结果如下:
注意,其实函数生成的数据类型不一定是固定的,看下面我们就知道了哈。
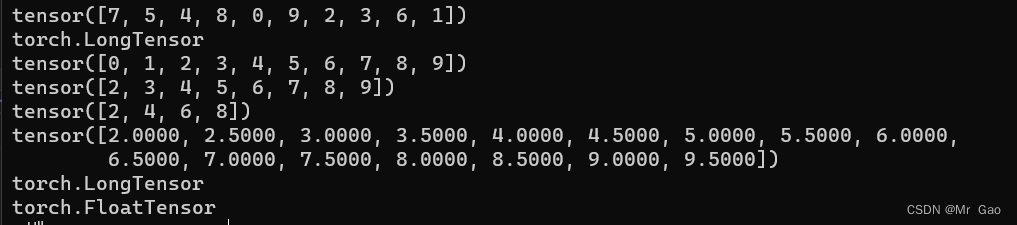 10.zeros,这个函数用法和ones很像,可以参考ones函数的用法。
10.zeros,这个函数用法和ones很像,可以参考ones函数的用法。
下面看代码:
print(torch.zeros(10))
print(torch.zeros(10).type())
返回一个全是0的张量,然后类型是FloatTensor,元素数量,由我们去传递。
输出结果如下:

11.zeros_like 这个会很据给定的一个张量生成与其维度一样的一个全0的张量。它可以生成任意维度哈。
看代码:
print(torch.zeros_like(a))
print(torch.zeros_like(b))
print(torch.zeros_like(a).type())
输出结果如下:

12 empty_like,用法与zeros_like类似,但是它生成的张量是未初始化的。
准确来说,生成的数据其实是有的,但是就是随机的。
a=torch.eye(2,3)
b=torch.ones(12)
print(torch.empty_like(a))
print(torch.empty_like(b))
print(torch.empty_like(a).type())
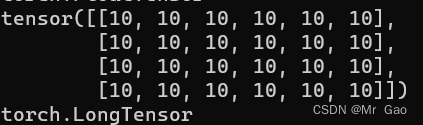
 13 full函数,传入一个维度s,再传入一个值v,会生成一个维度为s,值全为b的张量,
13 full函数,传入一个维度s,再传入一个值v,会生成一个维度为s,值全为b的张量,
代码如下:
print(torch.full((4,6),10))
print(torch.full((4,6),10).type())
输出如下:
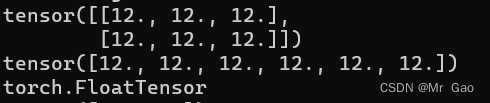
14 full_like ,和zeros_like很像啊,大家看代码。
a=torch.eye(2,3)
b=torch.ones(6)
print(torch.full_like(a))
print(torch.full_like(b))
print(torch.full_like(a).type())
输出结果如下:
15.as_tensor这个函数很重要,上面的十四个函数都很重要,但是这个比较重要,因为他是一个过渡函数,如果你以前对于列表、元组、ndarray学的比较好,那么这个函数对于你就比较实用,它可以直接进行类型的转化,将列表、元组、ndarray类型进行转化。
代码如下:
a=[1,2,3]
b=(1,2,3)
a2=[[1,2,3],[1,2,3]]
c=np.array([1,2,3])
print(torch.as_tensor(a))
print(torch.as_tensor(b))
print(torch.as_tensor(a2))
print(torch.as_tensor(c))
print(torch.as_tensor(a).type())
输出结果如下。
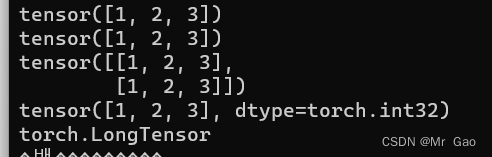
所以其实pytorch也是有规律的,一般都是转化为FloatTensor,只有一些整数会转化为LongTensor。
16 rand_like 和之前的full_lile,zeros_like,ones_like,类似,不过呢,这个返回的是0-1之间的随机数。
下面我们直接看代码:
a=torch.eye(2,3)
b=torch.ones(6)
print(torch.rand_like(a))
print(torch.rand_like(b))
print(torch.rand_like(a).type())
输出额结果如下:

17 randint,返回一个填充了随机整数的张量,我们需要设置随机整数的范围和张量维度。
示例代码如下:
print(torch.randint(0,10,size=(12,)))
print(torch.randint(0,10,size=(2,3)))
print(torch.randint(0,10,size=(2,3)).type())
注意要设置返回随机整数的范围,也就是传递上界和下界。
输出结果:

18 randint_like不用多说了把,看上面的都知道了
看看代码就懂了:
a=torch.eye(2,3)
b=torch.ones(6)
print(torch.randint_like(a,0,10))
print(torch.randint_like(b,0,10))
print(torch.randint_like(a,0,10).type())
输出结果如下:
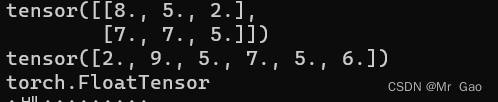
19.randn_like,这个也是一样的哈,根据输入张量形状返回的是正太分布的数据。
看代码:
a=torch.eye(2,3)
b=torch.ones(6)
print(torch.randn_like(a))
print(torch.randn_like(b))
print(torch.randn_like(a).type())
输出结果如下:

(2)通过tensor函数生成数据类型,这个函数上面应该是讲过了,但是这次主要将他的数据类型定义的这一块。
这个我们单拿出来做的,因为这个函数比较特别,它可以直接指定我们生成的数据类型。也可以说是非常非常重要的。
a = torch.tensor([3, 2], dtype=torch.float32)
print(a.type())
a = torch.tensor([3, 2], dtype=torch.int32)
print(a.type())
a = torch.tensor([3, 2], dtype=torch.int64)
print(a.type())
a = torch.tensor([3, 2], dtype=torch.float64)
print(a.type())
输出结果如下:
好的,到此,我们1.1算是完结了,大家学习一个数据结构一定是先从它如何产生的先学起,之后我们才能到其他的内容。
1.1的所有示例代码如下:
#coding=gbk
import os
import torch
import numpy as np
#使用torch函数生成torch数据类型
print(torch.randn(2,3))
print(torch.randn(2,3).type())
a=torch.randn(2,3)
print(a.type())
print(torch.rand(2,3))
print(torch.rand(2,3).type())
print(torch.eye(2,3))
print(torch.eye(2,3).type())
a=np.random.randn(2,3)
#print(a)
tor=torch.from_numpy(a)
print(tor)
print(tor.type())
print(torch.linspace(2,10,2))
print(torch.linspace(2,10,2).type())
print(torch.logspace(2,10,20))
print(torch.logspace(2,10,20).type())
#以5为底对数据进行对数处理,默认为10
print(torch.logspace(2,10,20,5))
print(torch.logspace(2,10,20,5).type())
print(torch.ones(10))
print(torch.ones(10).type())
print(torch.randperm(10))
print(torch.randperm(10).type())
print(torch.arange(10))
print(torch.arange(2,10))
print(torch.arange(2,10,2))
print(torch.arange(2,10,0.5))
print(torch.arange(10).type())
print(torch.arange(2,10,0.5).type())
print(torch.zeros(10))
print(torch.zeros(10).type())
a=torch.eye(2,3)
b=torch.ones(12)
print(torch.zeros_like(a))
print(torch.zeros_like(b))
print(torch.zeros_like(a).type())
a=torch.eye(2,3)
b=torch.ones(6)
print(torch.empty_like(a))
print(torch.empty_like(b))
print(torch.empty_like(a).type())
print(torch.full((4,6),10))
print(torch.full((4,6),10).type())
a=torch.eye(2,3)
b=torch.ones(6)
print(torch.full_like(a,12))
print(torch.full_like(b,12))
print(torch.full_like(a,12).type())
a=[1,2,3]
b=(1,2,3)
a2=[[1,2,3],[1,2,3]]
c=np.array([1,2,3])
print(torch.as_tensor(a))
print(torch.as_tensor(b))
print(torch.as_tensor(a2))
print(torch.as_tensor(c))
print(torch.as_tensor(a).type())
a=torch.eye(2,3)
b=torch.ones(6)
print(torch.rand_like(a))
print(torch.rand_like(b))
print(torch.rand_like(a).type())
print(torch.randint(0,10,size=(12,)))
print(torch.randint(0,10,size=(2,3)))
print(torch.randint(0,10,size=(2,3)).type())
a=torch.eye(2,3)
b=torch.ones(6)
print(torch.randint_like(a,0,10))
print(torch.randint_like(b,0,10))
print(torch.randint_like(a,0,10).type())
a=torch.eye(2,3)
b=torch.ones(6)
print(torch.randn_like(a))
print(torch.randn_like(b))
print(torch.randn_like(a).type())
os.system("pause")
对于1.1中提到的数据生成方法,基本都是可以选择存储设备的,device是选择gpu还是cpu,如果选择cpu,后面的运算也就由cpu执行,同理选择gpu就由gpu执行。所以大家可以根据自己的需求选择存储设备。
1.2 pytorch的各种数据类型有哪些属性?
这一部分的内容可能要轻松很多了哈,因为各个数据类型基本上属性都是共有的,所以,我们举一个就可以了。
下面我们该如何开始?
当然是先创建一个张量啦!这不就是我们1.1一直在讲的。
创建一个张量:
import os
import torch
import numpy as np
#使用torch函数生成torch数据类型
a=torch.randn(2,3)
- type 查看其数据类型
然后呢,查看他的数据类型是不是:
print(a.type())

那么第一个属性,就是数据类型这个属性,其实这也算是一个属性。
另外type其实应该是一个函数,应为它是可以调用的,具有小括号,它可以用来进行类型转换。
a=torch.randn(2,3)
print(a.type())
a = a.type(torch.int64)
print(a.type())
上面代码就可以进行类型转换,可以看出这个函数应该是又重新开辟了一段内存。
2.size 查看数据形状
用法也很简单:
a=torch.randn(2,3)
print(a.size())
a=torch.randn(2,)
print(a.size())
a=torch.randn(6)
print(a.size())
输出:
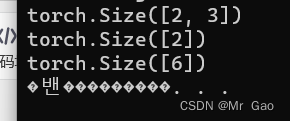
到这里,1.2其实就结束了,是的内从不多,因为属性是用来了解一个数据变量的,我们只需要通过type和size基本就可以知道这个变量的情况了。
1.2代码如下:
#coding=gbk
import os
import torch
import numpy as np
#使用torch函数生成torch数据类型
a=torch.randn(2,3)
print(a.type())
a = a.type(torch.int64)
print(a.type())
a=torch.randn(2,3)
print(a.size())
a=torch.randn(2,)
print(a.size())
a=torch.randn(6)
print(a.size())
os.system("pause")
1.3 pytorch的各种数据类型有哪些函数操作?
这里其实各种数据类型的函数操作基本都是一样的,无所谓增删改查,一些数值处理等等,那我们现在开始介绍:
1.is_tensor 和 is_storage。这是这样的,我们在生成一个tensor的时候,我们会得到一个tensor和其对应的变量,但是这个变量所指的地址并没有存储数据,而是存储了一些tensor的属性,比如type,size啊,还有它真实数据存储的地方。
那么我们生成一个变量呢,就会得到以恶搞tensor区和storage, tensor区存储tensor信息,storage区存储数据。如下图
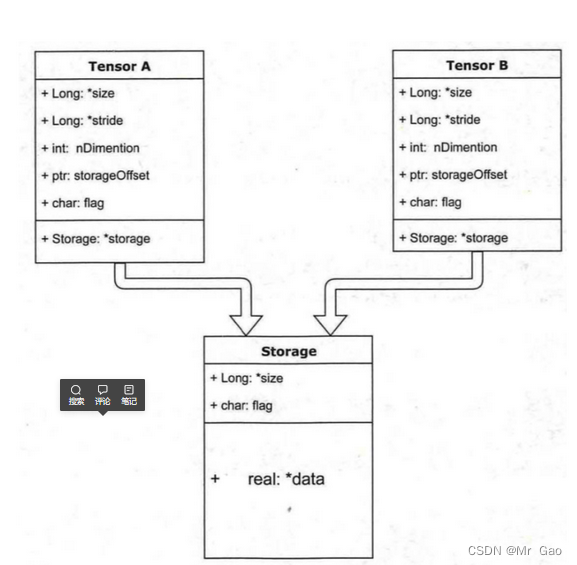
那么现在我们就看一下示例代码
a=torch.randn(2,3)
print(torch.is_tensor(a))
c=a.storage()
print(torch.is_storage(a))
print(torch.is_storage(c))
运行结果就会使下面这样:
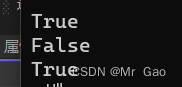
- numel 这个函数会返回张量总的的数据元素个数,也是很重要的,看下示例代码
a=torch.randn(2,3)
b=torch.randn(7)
print(torch.numel(a))
print(torch.numel(b))
输出结果就是6和7:

3. sparse_coo_tensor生成稀疏矩阵,稀疏矩阵之所以单拿出来用一个函数处理,因为pytorch肯定也是对其内存做了封装,对于存储稀疏矩阵有着处理。可以节省内存。
下面看一下这函数的用法,示例代码如下:
index=torch.tensor([[1,2],[2,1]])
value=torch.tensor([2,3],dtype=torch.float32)
t=torch.sparse_coo_tensor(index,value,(3,4))
print(t)
输出结果如下:

4.cat ,在给定维度上对输入的张量序列seq进行连接操作。这个函数会接受两个参数。
第一个参数tensors是你想要连接的若干个张量,按你所传入的顺序进行连接,注意每一个张量需要形状相同,或者更准确的说,进行行连接的张量要求列数相同,进行列连接的张量要求行数相同。
第二个参数dim表示维度,dim=0则表示按行连接,dim=1表示按列连接
来看一下示例代码:
a=torch.randn(2,3)
b=torch.randn(2,4)
c=torch.randn(4,3)
print(a)
print(b)
print(c)
print(torch.cat((a,b),1))
print(torch.cat((a,c),0))
输出结果如下:
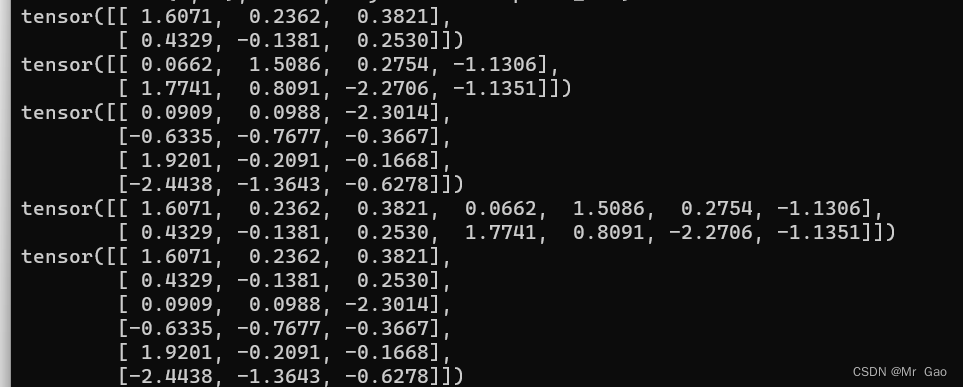
注意,第二个参数表示我们选择在那个轴上进行拼接,那个轴一定要相等。
5.chunk这个函数会对tensor进行分块处理。需要传入=三个参数,一个是tensor,一个是分块数量,还一个是按照那个轴进行分块。
下面我们看一下示例代码:
a=torch.randn(12,3)
print(torch.chunk(a,6,0))
a=torch.randn(3,12)
print(torch.chunk(a,6,1))
输出结果如下:
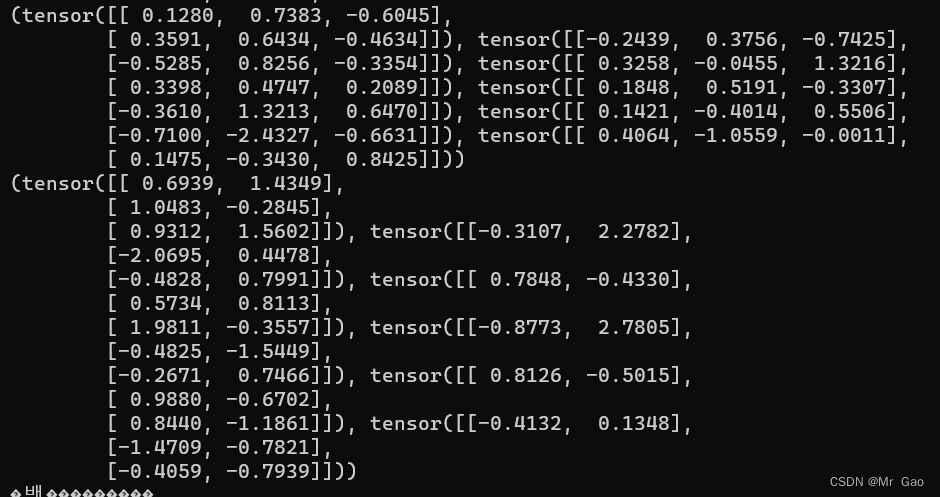
- gather,这个函数是做聚合的,其实就是从一个tensor中取出元素。
看一下示例用法
a=torch.randn(4,3)
index1=torch.LongTensor([[0,1,2,1]])
index2=torch.LongTensor([[0,1,2]])
print(a)
print(torch.gather(a,1,index1))
print(torch.gather(a,0,index2))
输出结果如下:
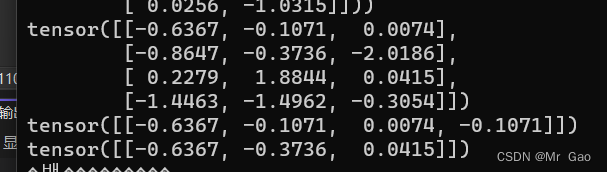
7.index_select,这个函数和上面那个差不多其实,但是gather选择的是元素,index_select选择的直接是一个小单元。
看一下示例代码
a=torch.randn(4,3)
index1=torch.LongTensor([0,1,2,1])
index2=torch.LongTensor([0,1,2])
print(a)
print(torch.index_select(a,1,index1))
print(torch.index_select(a,0,index2))
输出结果如下:
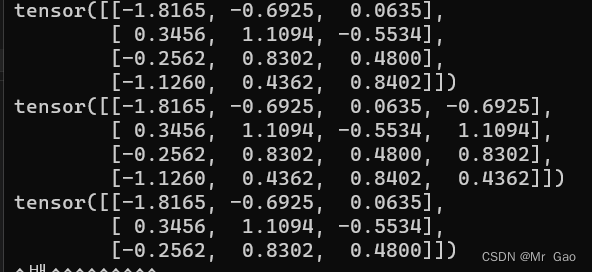
7.ge 函数,这函数传入一个tensor和一个数值v,会根据数值返回一个只含有不二数据的tensor,大于等于v返回true,小于返回false。
下面看示例代码
这个函数很重要哈,可以多学习学习。
a=torch.randint(0,10,(2,3))
print(a)
b=torch.ge(a,5)
print(b)
输出解结果如下:
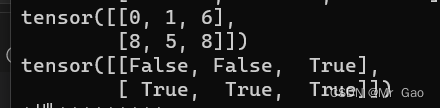
8.mask_index 其实我们将上面一个函数就是为了这个函数的讲解,这个函数传入两个张量,第二个张量的数据类型是bool类型的,根据第一个张量是否为true返回第二个tensor的元素。
下面看示例代码:
a=torch.randint(0,10,(2,3))
print(a)
b=torch.ge(a,5)
print(b)
print(torch.masked_select(a,b))
输出结果:
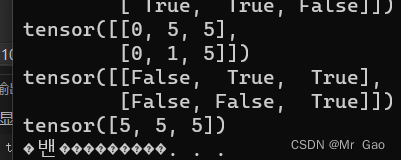
9.nonzero,这个函数需要出入一个张量,它会返回这个张量非0元素的索引。
看一下示例代码:
a=torch.randint(0,10,(2,3))
print(a)
print(torch.nonzero(a))
输出结果如下:
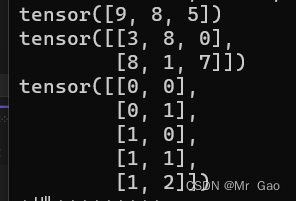
10.reshape,这个函数会改变张量的size
我们看一下示例代码:
a=torch.randint(0,10,(2,3))
b=a.reshape(3,2)
print(b)
b=a.reshape(6,1)
print(b)
b=a.reshape(1,6)
print(b)
b=a.reshape(6,)
print(b)
输出结果如下:
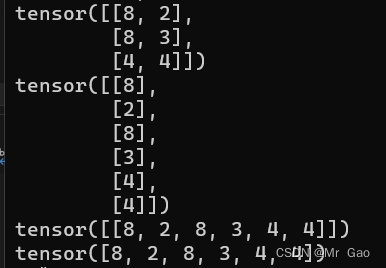
这个函数很重要哈,要好好掌握,所以给了三个例子。
11.split函数,这个函数跟前面的chunk很像,但是它又更灵活一点,它还可以传递列表进行切分
示例代码如下:
a=torch.randn(6,3)
print(a)
print(torch.split(a,3,0))
print(torch.split(a,[1,5],0))
a=torch.randn(3,6)
print(a)
print(torch.split(a,2,1))
输出结果如下:
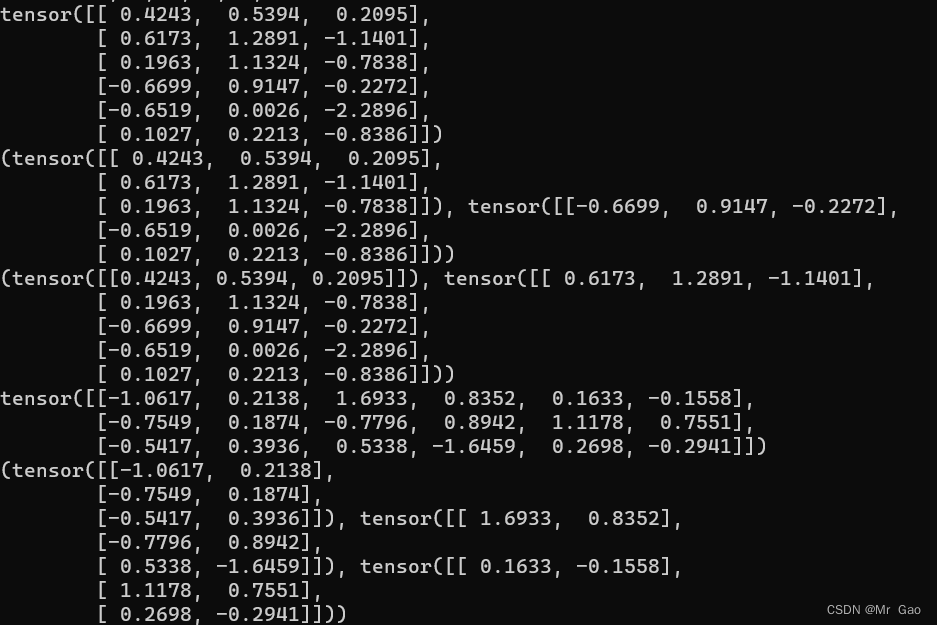
12.unsqueeze这个函数会对传入的张量进行维度扩充。
a=torch.randint(0,10,(2,3))
print(a)
b=torch.unsqueeze(a,0)
print(b)
b=torch.unsqueeze(a,1)
print(b)
这个函数可能会用的稍微少一点:
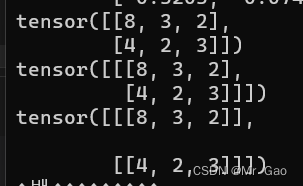
13 squeeze,这个函数用的就比较多了,它是一个降维的函数可以说。将输入张量形状中的1去除并返回。
看一下示例代码:
a=torch.randint(0,10,(2,3))
print(a)
b=torch.squeeze(a,0)
print(b)
a=torch.randint(0,10,(6,1))
b=torch.squeeze(a,0)
print(b)
输出结果如下:
注意只会把维度为1的那部分给压缩掉。
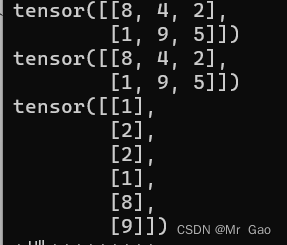
14.stack函数,这个会对数据进行一个拼接,跟cat函数有些类似。但是cat可以要求不同维度的张量进行拼接,stack必须同维度。
我们来看一下示例代码:
a=torch.randint(0,10,(2,3))
b=torch.randint(0,10,(2,3))
print(a)
print(b)
print(torch.stack((a,b),1))
print(torch.stack((a,b),0))
输出结果如下:
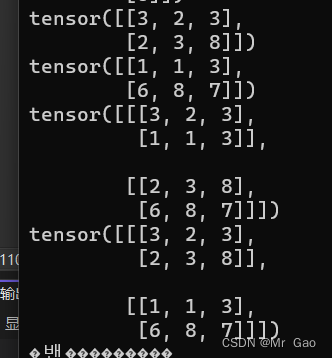
15.t函数,这个就是转置函数,这部分知识是矩阵里的。
示例代码如下:
a=torch.randint(0,10,(2,3))
print(a)
print(torch.t(a))
输出结果如下:
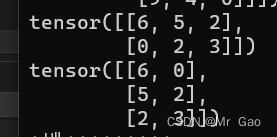
- transpose函数,这个函数其实是t函数的进阶版,可以任意选择两个维度进行交换处理。
a=torch.randint(0,10,(2,3))
print(a)
print(torch.transpose(a,0,1))
输出结果如下:
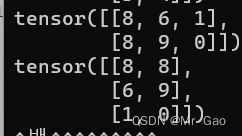
如果维度大于3的话,用这个比较好。
- unbind
移除指定维度后,返回一个元组,包含了沿着指定维切片后的各个切片。就是对传入的张量进行切分哈。
a=torch.randint(0,10,(2,3))
print(a)
print(torch.unbind(a,0))
print(torch.unbind(a,1))
会返回一个元组,根据传入的轴对tensor切分。
输出结果如下:

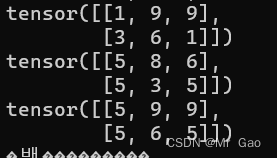
- where,这个函数比较特别在pytorch中,需要传入一个表达式,再传入两个张量,满足条件返回第一个张量的元素,不满足返回第二个张量的元素,这个函数应该听常用的平时,可以注意一下。
a=torch.randint(0,10,(2,3))
b=torch.randint(0,10,(2,3))
print(a)
print(b)
print(torch.where(a>5,a,b))
输出结果如下:
18. manual_seed和initial_seed,manual_seed会设置我们的随机种子,initial_seed则会返回,当前设置的随机种子。
看一下示例代码。
torch.manual_seed(10)
print(torch.initial_seed())
返回结果就是10。
随机种子设置好了,我们随机生成的数据就会固定了,那不就不随机了?主要还是做实验的时候,重复实验。
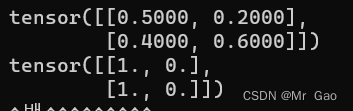
- bernoulli,做统计学的可能了解这个,这个呢,其实也是返回一个张量,输入参数为一个概率张量,元素值都要早0-1之间,这个函数会把输入的概率作为伯努利分布的概率参数,返回0,1值。看一下代码:
a=torch.tensor([[0.5,0.2],[0.4,0.6]])
print(a)
print(torch.bernoulli(a))
输出结果如下:
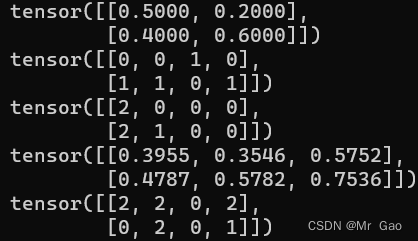
20 multinomial函数,多项式分布,什么意思呢,传入一个权重张量,然后会根据权重选择元素的下标,先看看代码,
a=torch.tensor([[0.5,0.2],[0.4,0.6]])
print(a)
print(torch.multinomial(a,4, replacement=True))
a=torch.rand(2,3)
print(torch.multinomial(a,4, replacement=True))
a=torch.rand(2,3)
print(a)
print(torch.multinomial(a,4, replacement=True))
输出结果就是下面这样,它返回的是整数值,其实是对应概率的下标,我们设置长度,就是这样。
- normal这个函数很重要,它是正太分布的函数,我们设置均值,方差之后,再设置维度,会生成对应参数的正太分布张量,来看代码。
print(torch.normal(0,1,(2,3)))
print(torch.normal(0,3,(2,3)))
输出结果:
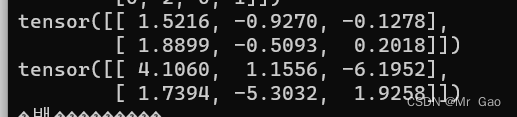
如果前两个参数传入0,1,就变成了randn了。
22.save,这个函数搞机器学习,神经网络肯定比较熟悉,没错,这就是我们深度学习,神经网络说的那个save,保存模型的那个函数。
下面我们看一下示例代码:
a=torch.rand(2,3)
torch.save(a,"tensor.pt")
torch.save(model,'net.pth')#保存网络结构和模型参数
torch.save(model.state_dict(),'net_params.pth')#只保存网络参数
对了,保存问见用pth,或者pt都可以没什么太大区别
- 讲完save,下一个讲什么?肯定是load了,这个是加载数据的。
看一下示例代码:
device=torch.device('cpu')
a=torch.load('tensor.pt',map_location=device)
print(a)
输出结果:

下面我们开始数学处理方面的一些函数
因为,博主看了一下基本大部分用法都一样, 而且使用起来简单多了,我这里就在代码里批量介绍了:
24.数学函数,元素直接处理
a=torch.randn(2,3)
print(a)
#绝对值处理
print(torch.abs(a))
a=torch.rand(2,3)
#反余弦处理
print(torch.acos(a))
#反正弦处理
print(torch.asin(a))
#正弦处理
print(torch.sin(a))
#正切处理
print(torch.tan(a))
#双曲正切处理
print(torch.tanh(a))
#双曲正弦处理
print(torch.sinh(a))
#反正切处理
print(torch.atan(a))
#向上取整
print(torch.ceil(a))
#exp处理
print(torch.exp(a))
#log处理
print(torch.log(a))
#log(a+1)处理
print(torch.log1p(a))
#取负处理
print(torch.neg(a))
#倒数处理
print(torch.reciprocal(a))
#得到除法余数
print(torch.remainder(a,0.2))
#张量元素分别加入一个值。
print(torch.add(a,10))#每个元素加10
#都除以一个数
print(torch.fmod(a,10))#每个元素除10
#向下取整
print(torch.floor(a))
#四舍五入处理
print(torch.round(a))
#平方根倒数
print(torch.rsqrt(a))
#sigmoid函数处理
print(torch.sigmoid(a))
#得到元素正负bool值
print(torch.sign(a))
#求平方根
print(torch.sqrt(a))
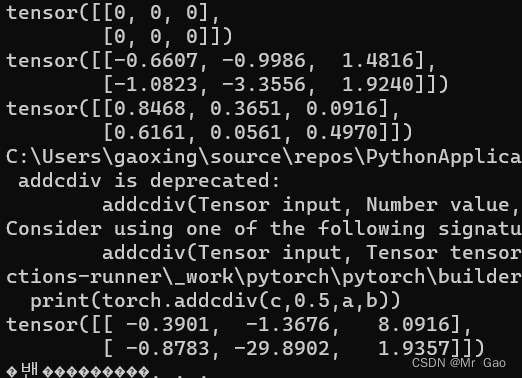
25.addcdiv 函数 ,用tensor2对tensor1逐元素相除,然后乘以标量值value并加到tensor上。
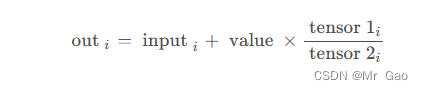
看一下示例代码:
c=torch.tensor([[0,0,0],[0,0,0]])
a=torch.randn(2,3)
b=torch.rand(2,3)
print(c)
print(a)
print(b)
print(torch.addcdiv(c,0.5,a,b))
输出结果如下:
26.addcmul 这个用法和上面一个函数很相似。看一下公式:
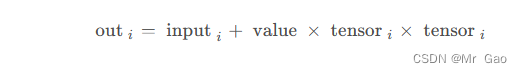
示例代码:
c=torch.tensor([[0,0,0],[0,0,0]])
a=torch.randn(2,3)
b=torch.rand(2,3)
print(c)
print(a)
print(b)
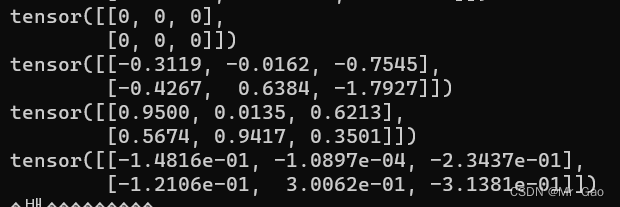
print(torch.addcmul(c,0.5,a,b))
输出结果:
27 lerp 线性插值处理,传入两个维度一样的张量,和一个权重值
公式:
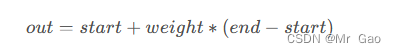
示例代码:
a=torch.randn(2,3)
b=torch.rand(2,3)
print(a)
print(b)
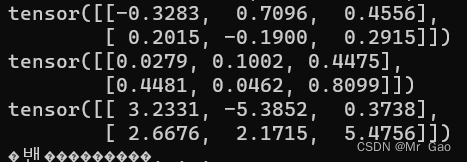
print(torch.lerp(a,b,10))
输出:
29 mul 传入两个维度一样的张量,按元素相乘。
a=torch.randn(2,3)
b=torch.rand(2,3)
print(a)
print(b)
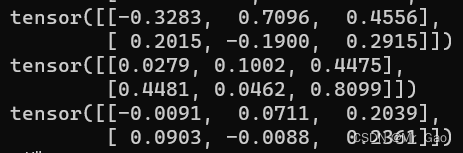
print(torch.mul(a,b))
输出结果如下:
29 cumprod,这个函数会进行累乘,不过我们设置轴的位置。
看一下示例代码:
a=torch.randint(1,4,(3,3))
print(a)
print(torch.cumprod(a,0))
print(torch.cumprod(a,1))
测试结果如下:
通过轴的设置,可以按行或者按列进行累乘。
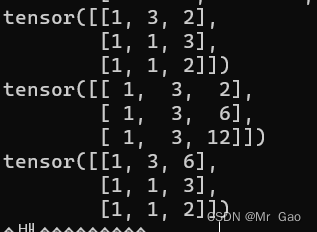
30 cumsum,这个函数和上面一个函数用法差不多,不过变成了累积。
示例代码:
a=torch.randint(1,4,(3,3))
print(a)
print(torch.cumsum(a,0))
print(torch.cumsum(a,1))
输出结果如下:
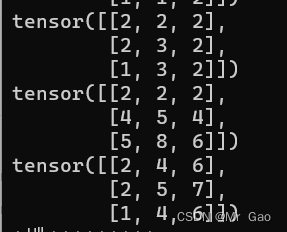
31.dist函数,可以济宁P函数计算,输入两个张量,会将两个张量相减后的张量求解范数结果。
看下范数求解公式:

示例代码如下:
a=torch.randint(1,5,(6,))
b=torch.randint(1,5,(6,))
a=a.type(dtype=torch.float32)
b=b.type(dtype=torch.float32)
print(a)
print(b)
print(torch.dist(a,b,2))
print(torch.dist(a,b,4))
a=torch.randint(1,5,(2,3))
b=torch.randint(1,5,(2,3))
a=a.type(dtype=torch.float32)
b=b.type(dtype=torch.float32)
print(a)
print(b)
print(torch.dist(a,b,2))
print(torch.dist(a,b,4))
这个函数很重要,大家好好掌握一下:
输出结果如下:
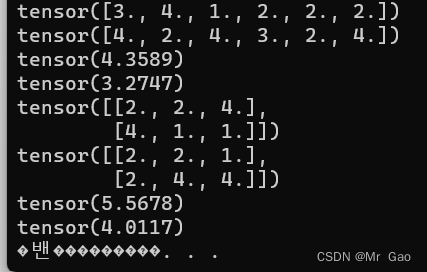
32 数学相关处理函数
下面就直接上代码,这个一块函数用法比较简单,大家运行一下下面代码就懂了。
a=torch.randint(1,4,(3,3))
print(a)
#求均值,第二个参数设置轴的方向,按行还是按列
print(torch.mean(a.type(dtype=torch.float32),0))
print(torch.mean(a.type(dtype=torch.float32),1))
#求中位数,第二个参数设置轴的方向,按行还是按列
print(torch.median(a,0))
print(torch.median(a,1))
#求众数
print(torch.mode(a,0))
print(torch.mode(a,1))
#求进行P范数求解,第二个为范数参数,第三个参数为轴的选择
print(torch.norm(a.type(dtype=torch.float32),2,0))
print(torch.norm(a.type(dtype=torch.float32),2,1))
#求累乘结果,第二个此参数设置轴
print(torch.prod(a.type(dtype=torch.float32),0))
print(torch.prod(a.type(dtype=torch.float32),1))
#求标准差
print(torch.std(a.type(dtype=torch.float32),0))
print(torch.std(a.type(dtype=torch.float32),1))
#求和
print(torch.sum(a,0))
print(torch.sum(a,1))
#求方差
print(torch.var(a.type(dtype=torch.float32),0))
print(torch.var(a.type(dtype=torch.float32),1))
#求最大值
print(torch.max(a,0))
print(torch.max(a,1))
#求最小值
print(torch.min(a,0))
print(torch.min(a,1))
#进行排序
print(torch.sort(a,0))
print(torch.sort(a,1))
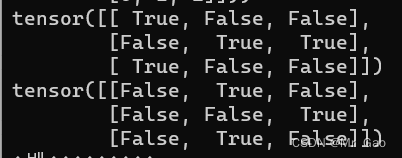
- 下面是一些比较操作函数 eq,传入两个参数第一个为张量,第二个为一个数或者一个张量,然后比较是否相等
看一下示例代码:
a=torch.randint(1,4,(3,3))
b=torch.randint(1,4,(3,3))
print(torch.eq(a,1))
print(torch.eq(a,b))
结果如下:
- equal这个函数就比较厉害了,就是比较两个张量是不是完全相等,我们看一下
a=torch.randint(1,4,(3,3))
b=torch.randint(1,4,(3,3))
print(torch.equal(a,b))
a=torch.tensor([[1,2,3]])
b=torch.tensor([[1,2,3]])
print(torch.equal(a,b))
b=b.type(dtype=torch.float32)
print(a.type())
print(b.type())
print(torch.equal(a,b))
输出结果:
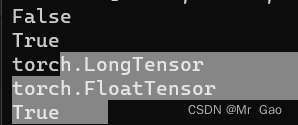
可以看出来,是不比较类型的,只是比较值是不是相等。维度是不是一样。
35. ge 这个函数就是比较两个张量大小的,ge(a,b),a>=b返回true,反之返回false。第二个参数可以是值或者张量。
看一下示例代码:
a=torch.randint(1,4,(3,3))
b=torch.randint(1,4,(3,3))
print(a)
print(b)
print(torch.ge(a,b))
输出结果如下:
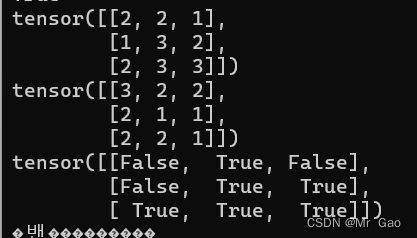
-
gt 这个函数也是比较两个张量大小的,但是等号去掉了,ge(a,b),a>b返回true,反之返回false。
这个不用示例代码了,更上面几乎差不多了。 -
le 这个函数也是比较两个张量大小的,le(a,b),a<=b返回true,反之返回false,注意是逐个元素比较,第二个参数可以是值或者张量。
-
lt 这个函数也是比较两个张量大小的,但是等号去掉了,lt(a,b),a<b返回true,反之返回false。,注意是逐个元素比较,第二个参数可以是值或者张量。
39 kthvalue,输入一个张量,输入一个k和dim,dim为选择的轴方向,k为取得第几个最小的值,第二个参数可以是值或者张量。
看一下示例代码:
a=torch.randint(1,4,(4,4))
print(a)
print(torch.kthvalue(a,2,0))
print(torch.kthvalue(a,2,1))
输出结果如下:
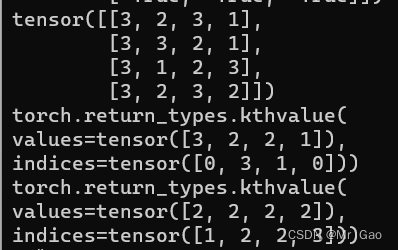
40 topk,输入一个张量,输入一个k和dim,dim为选择的轴方向,k为取得第几个最大的值。跟上面kthvalue很像。
a=torch.randint(1,4,(4,4))
print(a)
print(torch.topk(a,2,0))
print(torch.topk(a,2,1))
看一下示例代码
41.cross 叉积也称向量积这是线性代数里的知识。
向量积的计算公式如下图:
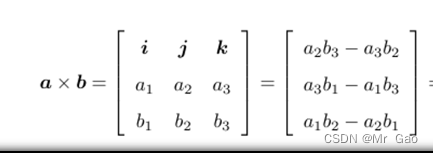
看一下示例代码:
a=torch.randint(1,4,(2,3))
b=torch.randint(1,4,(2,3))
print(a)
print(b)
print(torch.cross(a,b))
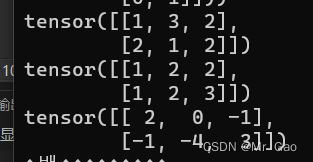
42.diag 如果输入是一个向量,则返回一个以input为对角线元素的2D方阵。如果输入是一个矩阵,则返回一个包含input为对角元素的1D张量。
看一下示例代码:
a=torch.randint(1,4,(2,3))
print(a)
print(torch.diag(a))
print(torch.diag(torch.tensor([1,2,3])))
输出结果如下:
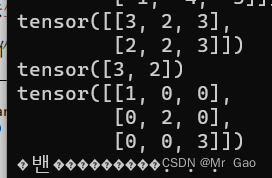
43 histc函数,进行区间统计,传入一个张量和区间数量,还有上下界,如果不传入上下界,默认使用张量中的最大值和最小值作为上下界。
示例代码如下:
a=torch.randint(1,10,(2,3))
print(a)
print(torch.histc(a.type(dtype=torch.float32),5))
a=torch.randint(1,10,(10,))
print(a)
print(torch.histc(a.type(dtype=torch.float32),5))
print(torch.histc(a.type(dtype=torch.float32),5,5,10))
输出结果如下:
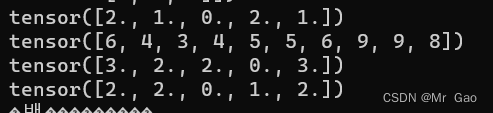
44.renorm,返回一个张量,包含规范化后的各个子张量,使得沿着dim维划分的各子张量的p范数小于maxnorm。如果p范数的值小于maxnorm,则当前子张量不需要修改。
看一下示例代码:
a=torch.randint(1,10,(2,3))
print(a)
print(torch.renorm(a.type(dtype=torch.float32),2,0,10))
print(torch.renorm(a.type(dtype=torch.float32),2,1,10))
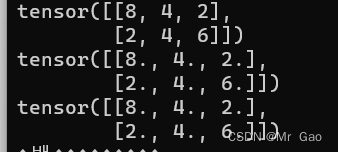
输出结果如下:
45. trace,输出二维矩阵对角线元素和
a=torch.randint(1,10,(2,3))
print(a)
print(torch.trace(a.type(dtype=torch.float32)))
注意,非方阵也可以求。
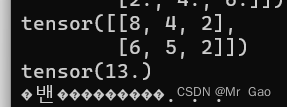
- tril 输入一个矩阵,返回一个将上三角元素全部置0的矩阵。
a=torch.randint(1,10,(3,3))
print(a)
print(torch.tril(a.type(dtype=torch.float32)))
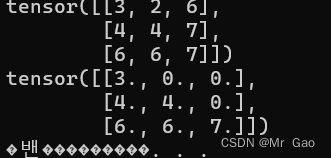
- triu输入一个矩阵,返回一个将下三角元素全部置0的矩阵。
a=torch.randint(1,10,(3,3))
print(a)
print(torch.triu(a.type(dtype=torch.float32)))
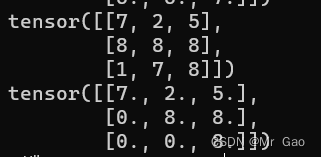
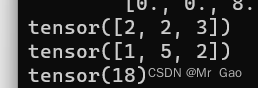
47. dot返回两个张量的点乘。
看一下示例代码:
a=torch.randint(1,10,(3,))
b=torch.randint(1,10,(3,))
print(a)
print(b)
print(torch.dot(a,b))
输出结果如下:
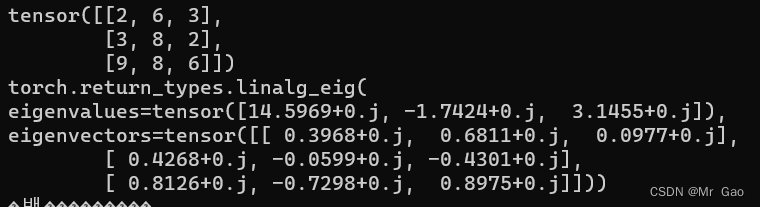
48. inalg.eig,求矩阵的特征值和特征向量,这个很重要哈。
看一下示例代码:
a=torch.randint(1,10,(3,3))
print(a)
print(torch.inalg.eig(a.type(dtype=torch.float32)))
输出结果如下:
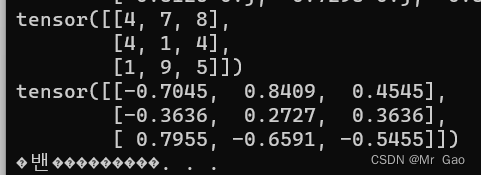
49. inverse,对矩阵求逆。
a=torch.randint(1,10,(3,3))
print(a)
print(torch.inverse(a.type(dtype=torch.float32)))
输出结果如下:
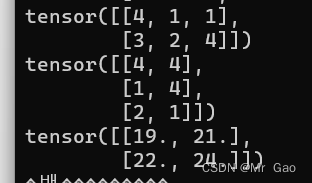
50 mm,进行矩阵相乘。
a=torch.randint(1,5,(2,3))
b=torch.randint(1,5,(3,2))
print(a)
print(b)
print(torch.mm(a.type(dtype=torch.float32),b.type(dtype=torch.float32)))
输出结果如下:
51. mv,矩阵和向量进行相乘。
a=torch.randint(1,5,(2,3))
b=torch.randint(1,5,(3,))
print(a)
print(b)
print(torch.mv(a.type(dtype=torch.float32),b.type(dtype=torch.float32)))
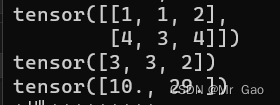
-
any ,当tensor存在一个元素为true 返回true,否则返回false。
-
all, 当tensor元全素为true 返回true,否则返回false。
到此我们1.3也算结束了,下面我们附上1.3全部的代码:
#coding=gbk
import os
import torch
import numpy as np
#使用torch函数生成torch数据类型
a=torch.randn(2,3)
print(torch.is_tensor(a))
c=a.storage()
print(torch.is_storage(a))
print(torch.is_storage(c))
a=torch.randn(2,3)
b=torch.randn(7)
print(torch.numel(a))
print(torch.numel(b))
index=torch.tensor([[1,2],[2,1]])
value=torch.tensor([2,3],dtype=torch.float32)
t=torch.sparse_coo_tensor(index,value,(3,4))
print(t)
a=torch.randn(2,3)
b=torch.randn(2,4)
c=torch.randn(4,3)
print(a)
print(b)
print(c)
print(torch.cat((a,b),1))
print(torch.cat((a,c),0))
a=torch.randn(12,3)
print(torch.chunk(a,6,0))
a=torch.randn(3,12)
print(torch.chunk(a,6,1))
a=torch.randn(4,3)
index1=torch.LongTensor([[0,1,2,1]])
index2=torch.LongTensor([[0,1,2]])
print(a)
print(torch.gather(a,1,index1))
print(torch.gather(a,0,index2))
a=torch.randn(4,3)
index1=torch.LongTensor([0,1,2,1])
index2=torch.LongTensor([0,1,2])
print(a)
print(torch.index_select(a,1,index1))
print(torch.index_select(a,0,index2))
a=torch.randint(0,10,(2,3))
print(a)
b=torch.ge(a,5)
print(b)
a=torch.randint(0,10,(2,3))
print(a)
b=torch.ge(a,5)
print(b)
print(torch.masked_select(a,b))
a=torch.randint(0,10,(2,3))
print(a)
print(torch.nonzero(a))
a=torch.randint(0,10,(2,3))
b=a.reshape(3,2)
print(b)
b=a.reshape(6,1)
print(b)
b=a.reshape(1,6)
print(b)
b=a.reshape(6,)
print(b)
a=torch.randn(6,3)
print(a)
print(torch.split(a,3,0))
print(torch.split(a,[1,5],0))
a=torch.randn(3,6)
print(a)
print(torch.split(a,2,1))
a=torch.randint(0,10,(2,3))
print(a)
b=torch.unsqueeze(a,0)
print(b)
b=torch.unsqueeze(a,1)
print(b)
a=torch.randint(0,10,(2,3))
print(a)
b=torch.squeeze(a,0)
print(b)
a=torch.randint(0,10,(6,1))
b=torch.squeeze(a,0)
print(b)
a=torch.randint(0,10,(2,3))
b=torch.randint(0,10,(2,3))
print(a)
print(b)
print(torch.stack((a,b),1))
print(torch.stack((a,b),0))
a=torch.randint(0,10,(2,3))
print(a)
print(torch.t(a))
a=torch.randint(0,10,(2,3))
print(a)
print(torch.transpose(a,0,1))
a=torch.randint(0,10,(2,3))
print(a)
print(torch.unbind(a,0))
print(torch.unbind(a,1))
a=torch.randint(0,10,(2,3))
b=torch.randint(0,10,(2,3))
print(a)
print(b)
print(torch.where(a>5,a,b))
torch.manual_seed(10)
print(torch.initial_seed())
a=torch.tensor([[0.5,0.2],[0.4,0.6]])
print(a)
print(torch.bernoulli(a))
a=torch.tensor([[0.5,0.2],[0.4,0.6]])
print(a)
print(torch.multinomial(a,4, replacement=True))
a=torch.rand(2,3)
print(torch.multinomial(a,4, replacement=True))
a=torch.rand(2,3)
print(a)
print(torch.multinomial(a,4, replacement=True))
print(torch.normal(0,1,(2,3)))
print(torch.normal(0,3,(2,3)))
a=torch.rand(2,3)
torch.save(a,"tensor.pt")
device=torch.device('cpu')
a=torch.load('tensor.pt',map_location=device)
print(a)
a=torch.randn(2,3)
print(a)
#绝对值处理
print(torch.abs(a))
a=torch.rand(2,3)
#反余弦处理
print(torch.acos(a))
#反正弦处理
print(torch.asin(a))
#正弦处理
print(torch.sin(a))
#正切处理
print(torch.tan(a))
#双曲正切处理
print(torch.tanh(a))
#双曲正弦处理
print(torch.sinh(a))
#反正切处理
print(torch.atan(a))
#向上取整
print(torch.ceil(a))
#exp处理
print(torch.exp(a))
#log处理
print(torch.log(a))
#取负处理
print(torch.neg(a))
#倒数处理
print(torch.reciprocal(a))
#得到除法余数
print(torch.remainder(a,0.2))
#张量元素分别加入一个值。
print(torch.add(a,10))#每个元素加10
#四舍五入处理
print(torch.round(a))
#平方根倒数
print(torch.rsqrt(a))
#sigmoid函数处理
print(torch.sigmoid(a))
#得到元素正负bool值
print(torch.sign(a))
#求平方根
print(torch.sqrt(a))
c=torch.tensor([[0,0,0],[0,0,0]])
a=torch.randn(2,3)
b=torch.rand(2,3)
print(c)
print(a)
print(b)
print(torch.addcdiv(c,0.5,a,b))
c=torch.tensor([[0,0,0],[0,0,0]])
a=torch.randn(2,3)
b=torch.rand(2,3)
print(c)
print(a)
print(b)
print(torch.addcmul(c,0.5,a,b))
a=torch.randn(2,3)
b=torch.rand(2,3)
print(a)
print(b)
print(torch.mul(a,b))
a=torch.randint(1,4,(3,3))
print(a)
print(torch.cumprod(a,0))
print(torch.cumprod(a,1))
a=torch.randint(1,4,(3,3))
print(a)
print(torch.cumsum(a,0))
print(torch.cumsum(a,1))
a=torch.randint(1,5,(6,))
b=torch.randint(1,5,(6,))
a=a.type(dtype=torch.float32)
b=b.type(dtype=torch.float32)
print(a)
print(b)
print(torch.dist(a,b,2))
print(torch.dist(a,b,4))
a=torch.randint(1,5,(2,3))
b=torch.randint(1,5,(2,3))
a=a.type(dtype=torch.float32)
b=b.type(dtype=torch.float32)
print(a)
print(b)
print(torch.dist(a,b,2))
print(torch.dist(a,b,4))
a=torch.randint(1,4,(3,3))
print(a)
#求均值,第二个参数设置轴的方向,按行还是按列
print(torch.mean(a.type(dtype=torch.float32),0))
print(torch.mean(a.type(dtype=torch.float32),1))
#求中位数,第二个参数设置轴的方向,按行还是按列
print(torch.median(a,0))
print(torch.median(a,1))
#求众数
print(torch.mode(a,0))
print(torch.mode(a,1))
#求进行P范数求解,第二个为范数参数,第三个参数为轴的选择
print(torch.norm(a.type(dtype=torch.float32),2,0))
print(torch.norm(a.type(dtype=torch.float32),2,1))
#求累乘结果,第二个此参数设置轴
print(torch.prod(a.type(dtype=torch.float32),0))
print(torch.prod(a.type(dtype=torch.float32),1))
#求标准差
print(torch.std(a.type(dtype=torch.float32),0))
print(torch.std(a.type(dtype=torch.float32),1))
#求和
print(torch.sum(a,0))
print(torch.sum(a,1))
#求方差
print(torch.var(a.type(dtype=torch.float32),0))
print(torch.var(a.type(dtype=torch.float32),1))
#求最大值
print(torch.max(a,0))
print(torch.max(a,1))
#求最小值
print(torch.min(a,0))
print(torch.min(a,1))
#进行排序
print(torch.sort(a,0))
print(torch.sort(a,1))
a=torch.randint(1,4,(3,3))
b=torch.randint(1,4,(3,3))
print(torch.eq(a,1))
print(torch.eq(a,b))
a=torch.randint(1,4,(3,3))
b=torch.randint(1,4,(3,3))
print(torch.equal(a,b))
a=torch.tensor([[1,2,3]])
b=torch.tensor([[1,2,3]])
print(torch.equal(a,b))
b=b.type(dtype=torch.float32)
print(a.type())
print(b.type())
print(torch.equal(a,b))
a=torch.randint(1,4,(3,3))
b=torch.randint(1,4,(3,3))
print(a)
print(b)
print(torch.ge(a,b))
a=torch.randint(1,4,(4,4))
print(a)
print(torch.kthvalue(a,2,0))
print(torch.kthvalue(a,2,1))
a=torch.randint(1,4,(4,4))
print(a)
print(torch.topk(a,2,0))
print(torch.topk(a,2,1))
a=torch.randint(1,4,(2,3))
b=torch.randint(1,4,(2,3))
print(a)
print(b)
print(torch.cross(a,b))
a=torch.randint(1,4,(2,3))
print(a)
print(torch.diag(a))
print(torch.diag(torch.tensor([1,2,3])))
a=torch.randint(1,10,(2,3))
print(a)
print(torch.histc(a.type(dtype=torch.float32),5))
a=torch.randint(1,10,(10,))
print(a)
print(torch.histc(a.type(dtype=torch.float32),5))
print(torch.histc(a.type(dtype=torch.float32),5,5,10))
a=torch.randint(1,10,(2,3))
print(a)
print(torch.renorm(a.type(dtype=torch.float32),2,0,10))
print(torch.renorm(a.type(dtype=torch.float32),2,1,10))
a=torch.randint(1,10,(2,3))
print(a)
print(torch.trace(a.type(dtype=torch.float32)))
a=torch.randint(1,10,(3,3))
print(a)
print(torch.tril(a.type(dtype=torch.float32)))
a=torch.randint(1,10,(3,3))
print(a)
print(torch.triu(a.type(dtype=torch.float32)))
a=torch.randint(1,10,(3,))
b=torch.randint(1,10,(3,))
print(a)
print(b)
print(torch.dot(a,b))
a=torch.randint(1,10,(3,3))
print(a)
print(torch.linalg.eig(a.type(dtype=torch.float32)))
a=torch.randint(1,10,(3,3))
print(a)
print(torch.inverse(a.type(dtype=torch.float32)))
a=torch.randint(1,5,(2,3))
b=torch.randint(1,5,(3,2))
print(a)
print(b)
print(torch.mm(a.type(dtype=torch.float32),b.type(dtype=torch.float32)))
a=torch.randint(1,5,(2,3))
b=torch.randint(1,5,(3,))
print(a)
print(b)
print(torch.mv(a.type(dtype=torch.float32),b.type(dtype=torch.float32)))
os.system("pause")
2.数据类型和其操作谈完,选择某一个方向开始学习和实践。
我们学完了知识下面肯定是要进行这个实践,但是pytorch可以选择的实践方向很多,不过最常用的方向是深度学习方向,博主也从这个方向开始讲解。
对于深度学习实践部分,我们需要开始从一下几个步骤开始:
2.1 求导
2.2 损失函数
2.3优化器
2.4线性回归代码实战
2.5 卷积神经网络实战
2.6 神经网络实战
2.7 RNN和LSTM实战
下面我们开始正文
2.1 求导
为什么要求导,其实是为了迭代我们的模型参数,一般使用梯度下降算法,那就需要求导来求解梯度,然后更新模型参数。
首先,我们知道,梯度是为了更新,那么说明设置的参数是可变的,那就是变量。pytorch就是提供了这个方便,我们可以使用
autograd中的Variable生成变量,这个变量可以保存其对应的梯度。
下面看一段Variable对象的生成代码
from torch.autograd import Variable
x = Variable(torch.randint(0,4,(2, 3)).type(dtype=torch.float32), requires_grad=True)
输出结果如下:

requires_grad=True是指保存梯度信息。
下面来看一段求解提取的代码:
print(x)
#进行x运算
y=x*x
out=y.mean()
print(y)
print(out)
out.backward()
print(x.grad)
输出结果如下:
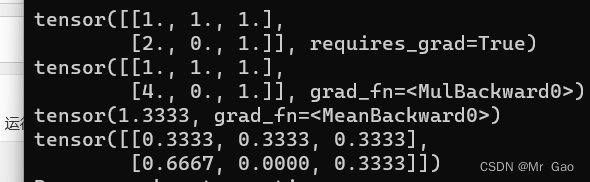
上面的函数就是out=sum(x*x)/len(x),对x逐个元素求平方之后求平均。
下面我们来看一个梯度更新的代码:
learning_rating=0.001
y_list=[]
def grad_update(x):
print("||")
print(x)
for i in range(1000):
y=x*x
out=torch.abs(y.sum())
print(out)
out.backward()
x.data=x.data-(learning_rating*x.grad.data)
# print(x.data)
y_list.append(out.data)
grad_update(x)
plt.plot(list(range(len(y_list))),y_list)
plt.show()
x再更新过程中,out的输出如下:
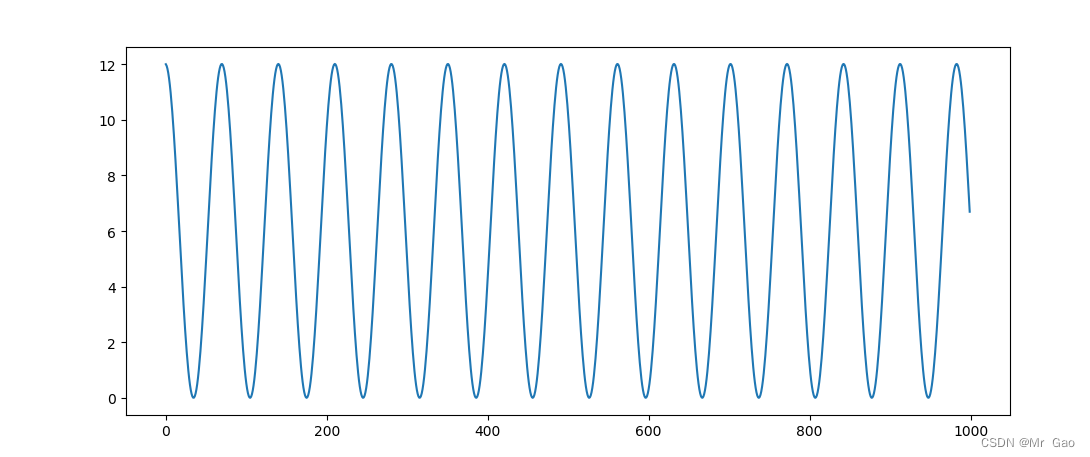
这个其实,出现了局部最优解的问题,是因为学习率设置的太大了。
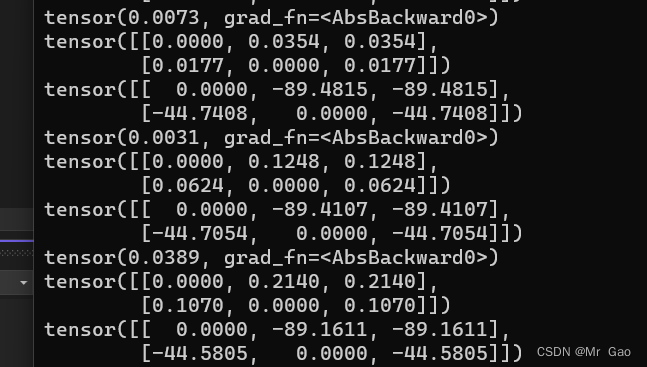
再快到达最低点的时候,有的参数变小了,有的参数变大了。然后直接跳过了最优点。
行,我们求导部分就到这啊。
2.1完整代码如下:
#coding=gbk
import os
import torch
import numpy as np
import matplotlib.pyplot as plt
#使用torch函数生成torch数据类型
from torch.autograd import Variable
x = Variable(torch.randint(0,4,(2, 3)).type(dtype=torch.float32), requires_grad=True)
print(x)
#进行x运算
y=x*x
out=y.mean()
print(y)
print(out)
out.backward()
print(x.grad.data)
learning_rating=0.000001
y_list=[]
def grad_update(x):
print("||")
print(x)
for i in range(1000):
y=x*x
out=torch.abs(y.sum())
print(out)
out.backward()
x.data=x.data-(learning_rating*x.grad.data)
# print(x.data)
y_list.append(out.data)
print(x.data)
print(x.grad.data)
grad_update(x)
plt.plot(list(range(len(y_list))),y_list)
plt.show()
2.2 损失函数
下面我们到第二部分损失函数的内容。
定义损失函数之前,我们当然要先定义两个张量,才能使损失函数生效,一个就是目标张量,一个是预测张量。
import os
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
#使用torch函数生成torch数据类型
from torch.autograd import Variable
predict = Variable(torch.randint(0,4,(2, 3)).type(dtype=torch.float32), requires_grad=True)
a=torch.Tensor([[1,2,2],[1,1,2]])
target = Variable (a)
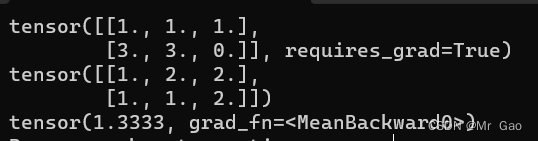
(1)那现在我们看第一个损失函数nn.L1Loss,取预测值和真实值的绝对误差的平均数。
print(predict)
print(target)
criterion = nn.L1Loss()
loss = criterion(predict, target)
看一下输出结果:
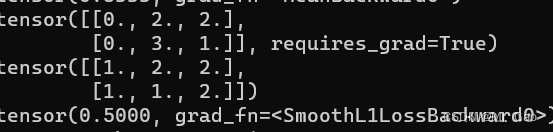
(2)nn.SmoothL1Loss损失函数,误差在 (-1,1) 上是平方损失,其他情况按L1Loss损失处理。
print(predict)
print(target)
criterion = nn.SmoothL1Loss()
loss = criterion(predict, target)
输出结果:
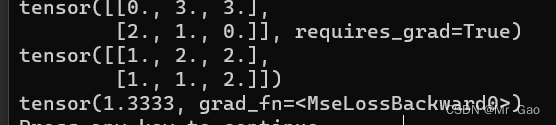
(3)nn.MSELoss损失函数,平方损失函数。其计算公式是预测值和真实值之间的平方和的平均数。
print(predict)
print(target)
criterion = nn.MSELoss()
loss = criterion(predict, target)
print(loss)
输出结果如下:
(4)nn.CrossEntropyLoss,交叉熵损失函数
交叉熵损失函数计算公式如下:
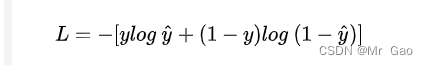
代码都是一样的了
print(predict)
print(target)
criterion = nn.CrossEntropyLoss()
loss = criterion(predict, target)
print(loss)
(5)nn.NLLLoss,负对数似然损失函数。
计算公式如下:
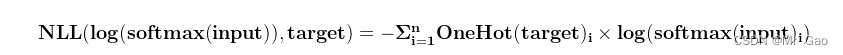
这个函数一般再图像里常用。
m = nn.LogSoftmax(dim=1) #横向计算
loss = nn.NLLLoss()
torch.manual_seed(2)
# 3行5列的输入,即3个样本各包含5个特征,每个样本通过softmax产生5个输出
input = torch.randn(3, 5, requires_grad=True)
target = torch.tensor([1, 0, 4])
# NLL将取输出矩阵中第0行的第1列、第1行的第0列、第2行的第4列加负号求和
output = loss(m(input), target)
这里就介绍这几个常用的,在实践中,我们会慢慢的用到,bong熟练掌握的。
2.2完整示例代码如下:
#coding=gbk
import os
import torch
import numpy as np
import matplotlib.pyplot as plt
#使用torch函数生成torch数据类型
import torch.nn as nn
from torch.autograd import Variable
predict = Variable(torch.randint(0,4,(2, 3)).type(dtype=torch.float32), requires_grad=True)
a=torch.Tensor([[1,2,2],[1,1,2]])
target = Variable (a)
print(predict)
print(target)
criterion = nn.L1Loss()
loss = criterion(predict, target)
print(loss)
print(predict)
print(target)
criterion = nn.SmoothL1Loss()
loss = criterion(predict, target)
print(loss)
print(predict)
print(target)
criterion = nn.MSELoss()
loss = criterion(predict, target)
print(loss)
print(predict)
print(target)
criterion = nn.CrossEntropyLoss()
loss = criterion(predict, target)
print(loss)
m = nn.LogSoftmax(dim=1) #横向计算
loss = nn.NLLLoss()
torch.manual_seed(2)
# 3行5列的输入,即3个样本各包含5个特征,每个样本通过softmax产生5个输出
input = torch.randn(3, 5, requires_grad=True)
target = torch.tensor([1, 0, 4])
# NLL将取输出矩阵中第0行的第1列、第1行的第0列、第2行的第4列加负号求和
output = loss(m(input), target)
print(output)
2.3优化器
优化器用通俗的话来说就是一种算法,是一种计算导数的算法。各种优化器的目的和发明它们的初衷其实就是能让用户选择一种适合自己场景的优化器。优化器的最主要的衡量指标就是优化曲线的平稳度,最好的优化器就是每一轮样本数据的优化都让权重参数匀速的接近目标值,而不是忽上忽下跳跃的变化。因此损失值的平稳下降对于一个深度学习模型来说是一个非常重要的衡量指标
(1)SGD优化器,批量随机梯度下降函数,随机选取部分数据集参与计算,是梯度下降的 batch 版本。
就是选择batch个样本,求解共同的损失去更新模型。
SGD的公式:
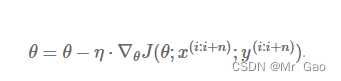
动量(Momentum)公式:
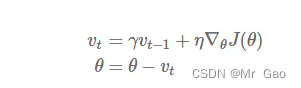
γ \gamma γ是动量传递参数。
使用代码如下:
from troch import optim
optimizer = optim.SGD(model.parameters(), lr = 0.01, momentum=0.9)
这个函数batch的处理,是我们自己事先处理好的,这个函数并不会处理。
(2)RMSprop优化器,这个优化器其实也是自适应调节学习率
来看一下他的更新公式:
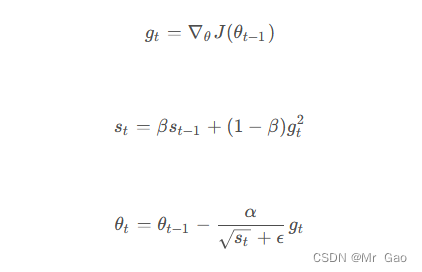
其中,
g
t
表示在
t
时刻的梯度,
s
t
s
表示
t
时刻的梯度平方的移动平均数,
β
是移动平均系数,一般取值为
0.9
,
α
是学习率,
ϵ
是一个极小值,以避免分母为
0
。
其中, g_t 表示在 t 时刻的梯度, s_t s 表示 t 时刻的梯度平方的移动平均数, \beta 是移动平均系数,一般取值为 0.9, \alpha 是学习率, \epsilon 是一个极小值,以避免分母为 0。
其中,gt表示在t时刻的梯度,sts表示t时刻的梯度平方的移动平均数,β是移动平均系数,一般取值为0.9,α是学习率,ϵ是一个极小值,以避免分母为0。
使用代码如下:
torch.optim.RMSprop(params,
lr=0.01,
alpha=0.99,
eps=1e-08,
weight_decay=0,
momentum=0,
centered=False)
(3)AdaGrad 优化器
AdaGrad 可以自动变更学习速率,只是需要设定一个全局的学习速率ϵ,但是这并非是实际学习速率,实际的速率是与以往参数的模之和的开方成反比的。也许说起来有点绕口,不过用公式来表示就直白的多:其中 δ 是一个很小的常亮,大概在 10-7,防止出现除以 0 的情况.。
具体实现:
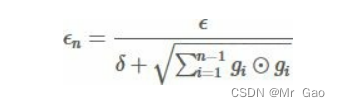
需要:全局学习速率 ϵ,初始参数 θ,数值稳定量 δ 。
中间变量:梯度累计量 r(初始化为 0) 。
每步迭代过程:
- 从训练集中的随机抽取一批容量为 m 的样本 {x1,…,xm} 以及相关
的输出 yi 。 - 计算梯度和误差,更新r,再根据 r 和梯度计算参数更新量 。
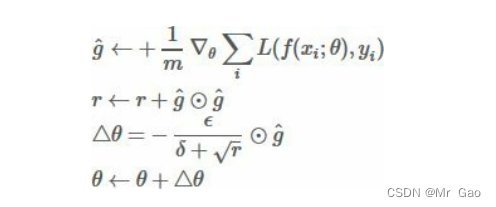
使用代码:
torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)
(4)Adadelta优化器,看一下怎么实现
先看第一个公式:
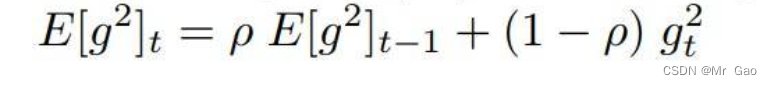
这里更新参数使用梯度的期望,计算公式如上式。
然后再开方得到梯度期望的开方,ϵ是防止分母为0的常数:
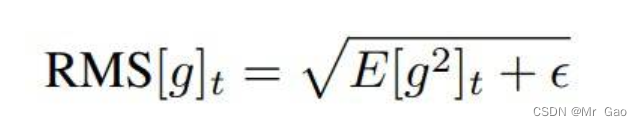
之后,对于t状态下,参数更新量为:
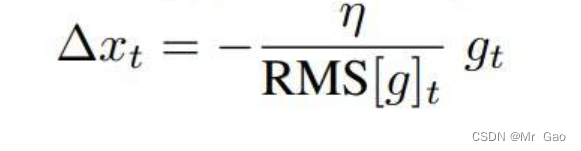
最终的更新公式则为:
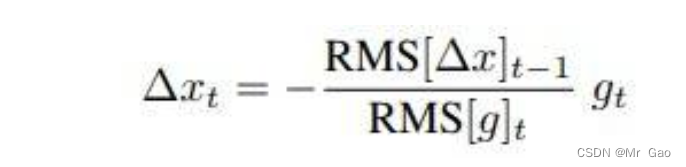
Adadelta优化器主要是采用期望的方法去更新梯度,考虑一个滑动窗口w,对这个窗口状态内每次得参数更新,梯度都进行考虑,这样使得更新情况更加稳定。
使用代码如下:
keras.optimizers.Adadelta(lr=1.0, rho=0.95, epsilon=1e-06)
(5)Adam优化器
更新公式如下:
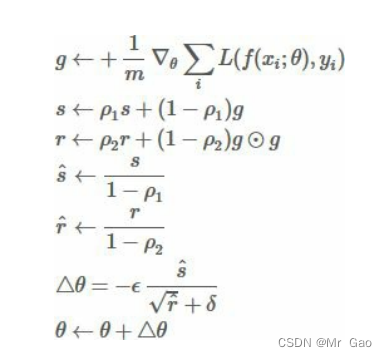
所以我们需要传入学习率,还有其他两个参数,r和s
调用方法如下:
torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
(6)Adamax优化器
更新公式如下:
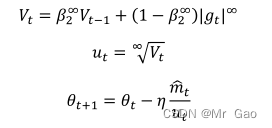
我们一般只需要设置以下三个参数,默认为:
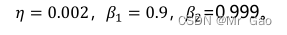
使用代码:
torch.optim.Adamax(params, lr=0.002, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
优化器这里,其实优化器对于我们模型性能一般情况下不会有太大的帮助,优化器做的更多的是,加速我们求解最优解,和防止出现局部最优解。
2.4线性回归代码实战
因为线性回归比较简单,所以我们可以自己去模拟数据,为了实验可以重复,我们首先要设置一个随机种子。
并导入相关依赖包
torch.import os
import torch
from torch.utils import data
import numpy as np
import matplotlib.pyplot as plt
from numpy import random
#使用torch函数生成torch数据类型
import torch.nn as nn
from torch.autograd import Variable
torch.manual_seed(1)
下面我们生成随机数据,其实就是生成一组数据,然后对x进行线性处理,之后加入噪声。
X = np.linspace(-1, 1, 200)
Y = 0.5 * X + 0.2* np.random.normal(0, 0.5, (200, ))
plt.scatter(X,Y)
plt.show()
#将X,Y转成200 batch大小,1维度的数据
X=Variable(torch.Tensor(X.reshape(200,1)))
Y=Variable(to
会画出一个图:
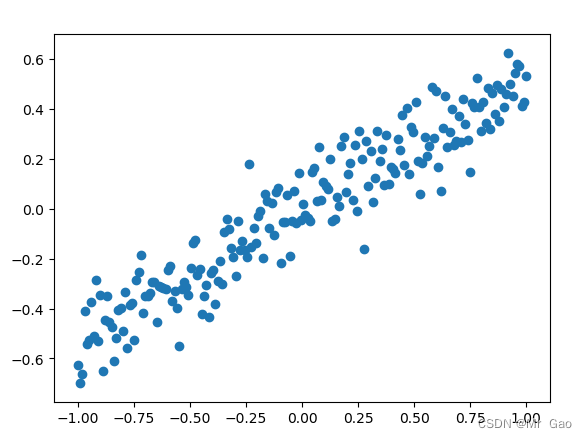
上面是生成的数据比较简单。
然后看模型求解代码:
model = torch.nn.Sequential(torch.nn.Linear(1, 1),)#输出结果为1,输出结果也为1
optimizer = torch.optim.SGD(model.parameters(), lr=0.5)
loss_function = torch.nn.MSELoss()
for i in range(300):
prediction = model(X)
loss = loss_function(prediction, Y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
plt.figure(1, figsize=(5, 5))
plt.title('model')
plt.scatter(X.data.numpy(), Y.data.numpy())
plt.plot(X.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
plt.show()
得到线性模型如下:
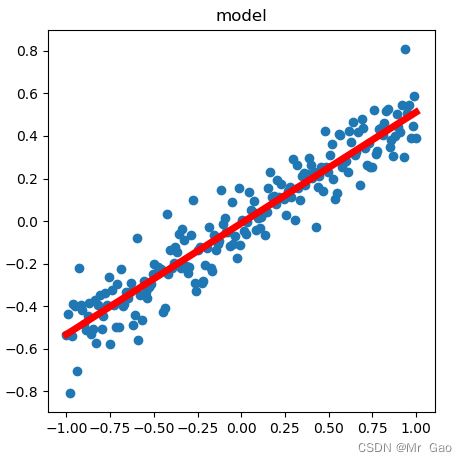
上面这个示例比较简单,下面我们来个多元线性回归。但是多元回归没法用图像显示,我们就求解他的loss去看看结果。
直接上代码:
X =torch.randn(100,4)
w=torch.tensor([1,2,3,4])
Y =torch.matmul(X, w.type(dtype=torch.float)) + torch.normal(0, 0.1, (100, ))+6.5
Y=Y.reshape((-1, 1))
print(Y.type())
print(w.type())
print(X.type())
#将X,Y转成200 batch大小,1维度的数据
X=Variable(X)
Y=Variable(Y)
def load_array(data_arrays, batch_size, is_train=True):
dataset = data.TensorDataset(*data_arrays)
return data.DataLoader(dataset, batch_size, shuffle=is_train)
data_iter = load_array((X, Y), 32)
model = torch.nn.Sequential(torch.nn.Linear(4, 1))
optimizer = torch.optim.SGD(model.parameters(), lr=0.03)
loss_function = torch.nn.MSELoss()
num_epochs = 20
for epoch in range(num_epochs):
for x, y in data_iter:
l = loss_function(model(x), y)
optimizer.zero_grad()
l.backward()
optimizer.step()
l = loss_function(model(X), Y)
print(f'epoch {epoch + 1}, loss {l:f}')
for para in model.parameters():
print(para)
这个是一个线性回归,四元线性回归。
看一下输出结果吧:

模型的参数,和我们设定的几乎一样,我想说的是,上面的代码其实严格意义上才算是一个完整的机器学习代码,一开始的其实没有用到SGD算法。
而且不用SGD算法的和用SGD算法的,两者的区别天差地别。
这个线性回归的代码我们就到这了啊。
下面附上完整代码:
#coding=gbk
import os
import torch
import numpy as np
import matplotlib.pyplot as plt
from torch.utils import data
from numpy import random
#使用torch函数生成torch数据类型
import torch.nn as nn
from torch.autograd import Variable
torch.manual_seed(1)
X = np.linspace(-1, 1, 200)
Y = 0.5 * X + 0.2* np.random.normal(0, 0.5, (200, ))
#plt.scatter(X,Y)
#plt.show()
#将X,Y转成200 batch大小,1维度的数据
X=Variable(torch.Tensor(X.reshape(200,1)))
Y=Variable(torch.Tensor(Y.reshape(200,1)))
model = torch.nn.Sequential(torch.nn.Linear(1, 1),)
optimizer = torch.optim.SGD(model.parameters(), lr=0.5)
loss_function = torch.nn.MSELoss()
for i in range(300):
prediction = model(X)
loss = loss_function(prediction, Y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
#plt.figure(1, figsize=(5, 5))
#plt.title('model')
#plt.scatter(X.data.numpy(), Y.data.numpy())
#plt.plot(X.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
#plt.show()
X =torch.randn(100,4)
w=torch.tensor([1,2,3,4])
Y =torch.matmul(X, w.type(dtype=torch.float)) + torch.normal(0, 0.1, (100, ))+6.5
Y=Y.reshape((-1, 1))
print(Y.type())
print(w.type())
print(X.type())
#将X,Y转成200 batch大小,1维度的数据
X=Variable(X)
Y=Variable(Y)
def load_array(data_arrays, batch_size, is_train=True):
dataset = data.TensorDataset(*data_arrays)
return data.DataLoader(dataset, batch_size, shuffle=is_train)
data_iter = load_array((X, Y), 32)
model = torch.nn.Sequential(torch.nn.Linear(4, 1))
optimizer = torch.optim.SGD(model.parameters(), lr=0.03)
loss_function = torch.nn.MSELoss()
num_epochs = 20
for epoch in range(num_epochs):
for x, y in data_iter:
l = loss_function(model(x), y)
optimizer.zero_grad()
l.backward()
optimizer.step()
l = loss_function(model(X), Y)
print(f'epoch {epoch + 1}, loss {l:f}')
for para in model.parameters():
print(para)
2.5 卷积神经网络实战
卷积神经网络,其实无外乎都是一个模式:
下面就是一个经典模型,先卷积,再进行ReLU函数处理,然后,再池化得到我们最后想要的特征图。
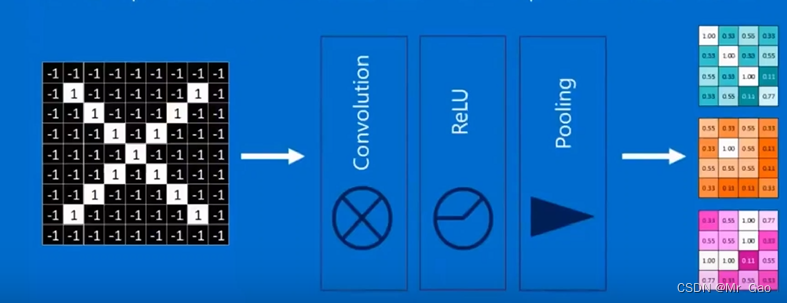
然后卷积之后的矩阵大小计算公式如下:
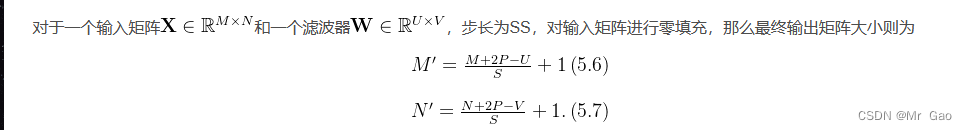
首先,我们先导入相关依赖包,然后加载数据集:
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
# 设备配置
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
# 超参数
# MNIST 数据集
train_dataset = torchvision.datasets.MNIST(root='../../data/',
train=True,
transform=transforms.ToTensor(),
download=True)
test_dataset = torchvision.datasets.MNIST(root='../../data/',
train=False,
transform=transforms.ToTensor())
# 数据加载器
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
下面我们定义网络:
class ConvNet(nn.Module):
def __init__(self, num_classes=10):
super(ConvNet, self).__init__()
self.layer1 = nn.Sequential(
nn.Conv2d(1, 16, kernel_size=5, stride=1, padding=2),
nn.BatchNorm2d(16),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2))
self.layer2 = nn.Sequential(
nn.Conv2d(16, 32, kernel_size=5, stride=1, padding=2),
nn.BatchNorm2d(32),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2))
self.fc = nn.Linear(7*7*32, num_classes)
def forward(self, x):
out = self.layer1(x)#1x28x28->16x14x14
out = self.layer2(out)#16x14x14->32x7x7
out = out.reshape(out.size(0), -1)
out = self.fc(out)
return out
定义损失函数和优化器:
# 损失和优化器
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
训练模型和测试模型:
# 训练模型
total_step = len(train_loader)
for epoch in range(num_epochs):
for i, (images, labels) in enumerate(train_loader):
images = images.to(device)
labels = labels.to(device)
# 前向传播
outputs = model(images)
loss = criterion(outputs, labels)
# 向后优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (i+1) % 100 == 0:
print ('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}'
.format(epoch+1, num_epochs, i+1, total_step, loss.item()))
# 测试模型
model.eval() # eval mode (batchnorm uses moving mean/variance instead of mini-batch mean/variance)
with torch.no_grad():
correct = 0
total = 0
for images, labels in test_loader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Test Accuracy of the model on the 10000 test images: {} %'.format(100 * correct / total))
保存模型:
# 保存模型
torch.save(model.state_dict(), 'model.ckpt')
这个示例是很典型的例子。
下面附上完整代码:
#coding=gbk
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
#定义超参数
num_epochs = 5
num_classes = 10
batch_size = 32
learning_rate = 0.001
# 设备配置
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
# MNIST 数据集
train_dataset = torchvision.datasets.MNIST(root='../../data/',
train=True,
transform=transforms.ToTensor(),
download=True)
test_dataset = torchvision.datasets.MNIST(root='../../data/',
train=False,
transform=transforms.ToTensor())
# 数据加载器
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
class ConvNet(nn.Module):
def __init__(self, num_classes=10):
super(ConvNet, self).__init__()
self.layer1 = nn.Sequential(
nn.Conv2d(1, 16, kernel_size=5, stride=1, padding=2),
nn.BatchNorm2d(16),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2))
self.layer2 = nn.Sequential(
nn.Conv2d(16, 32, kernel_size=5, stride=1, padding=2),
nn.BatchNorm2d(32),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2))
self.fc = nn.Linear(7*7*32, num_classes)
def forward(self, x):
out = self.layer1(x)#1x28x28->
out = self.layer2(out)
out = out.reshape(out.size(0), -1)
out = self.fc(out)
return out
model = ConvNet(num_classes).to(device)
# 损失和优化器
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
# 训练模型
total_step = len(train_loader)
for epoch in range(num_epochs):
for i, (images, labels) in enumerate(train_loader):
images = images.to(device)
labels = labels.to(device)
# 前向传播
outputs = model(images)
loss = criterion(outputs, labels)
# 向后优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (i+1) % 100 == 0:
print ('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}'
.format(epoch+1, num_epochs, i+1, total_step, loss.item()))
# 测试模型
model.eval() # eval mode (batchnorm uses moving mean/variance instead of mini-batch mean/variance)
with torch.no_grad():
correct = 0
total = 0
for images, labels in test_loader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Test Accuracy of the model on the 10000 test images: {} %'.format(100 * correct / total))
# 保存模型
torch.save(model.state_dict(), 'model.ckpt')
这个结果很棒:
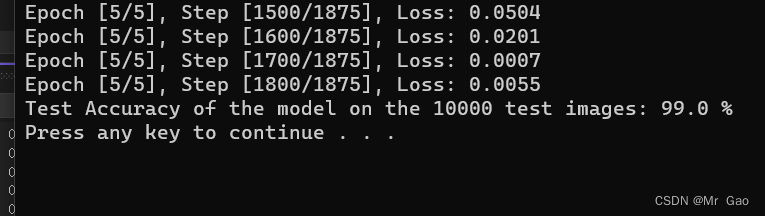
2.6神经网络实战
下面我们就开始使用pytorch进行神经网络的实战。
其实神经网络比卷积神经网络简单多了啊。
这里我们也用minist数据集进行测试,思路是这样的,对图片进行展平,形成一个784的长向量,然后,我们再搭建一个200神经元的隐藏层和10神经元的全连接层输出分类。用sigmoid作为激活函数。
下面看代码
第一步导入相关库,加载数据集,设置超参数:
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
#定义超参数
num_epochs = 5
num_classes = 10
batch_size = 32
learning_rate = 0.001
# 设备配置
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
# MNIST 数据集
train_dataset = torchvision.datasets.MNIST(root='../../data/',
train=True,
transform=transforms.ToTensor(),
download=True)
test_dataset = torchvision.datasets.MNIST(root='../../data/',
train=False,
transform=transforms.ToTensor())
# 数据加载器
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
定义模型结构,优化器,损失函数:
class Classifier(nn.Module):
def __init__(self):
# 初始化PyTorch父类
super().__init__()
# 定义神经网络层
self.model = nn.Sequential(
nn.Linear(784, 200),
nn.Sigmoid(),
nn.Linear(200, 10),
nn.Sigmoid()
)
# 创建损失函数
def forward(self, inputs):
# 直接运行模型
inputs=inputs.reshape(-1,784)
return self.model(inputs)
model = Classifier().to(device)
criterion=nn.MSELoss()
optimizer= torch.optim.SGD(model.parameters(), lr=0.01)
训练模型和测试模型:
# 训练模型
total_step = len(train_loader)
for epoch in range(num_epochs):
for i, (images, labels) in enumerate(train_loader):
images = images.to(device)
labels = labels.to(device)
# 前向传播
outputs = model(images)
# print(outputs)
loss=0
p=0
for j in labels:
label=torch.tensor([0,0,0,0,0,0,0,0,0,0])
label[j]=1
label=label.type(dtype=torch.float)
label = label.to(device)
# print(label)
loss = criterion(outputs[p], label)+loss
p=p+1
# 向后优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
# print(i)
if (i+1) % 100 == 0:
print ('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}'
.format(epoch+1, num_epochs, i+1, total_step, loss.item()))
# 测试模型
model.eval() # eval mode (batchnorm uses moving mean/variance instead of mini-batch mean/variance)
with torch.no_grad():
correct = 0
total = 0
for images, labels in test_loader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
loss=0
p=0
for j in labels:
label=torch.tensor([0,0,0,0,0,0,0,0,0,0])
label[j]=1
label=label.type(dtype=torch.float)
label = label.to(device)
if outputs[p].argmax()==label[j]:
correct=correct+1
# print(label)
loss = criterion(outputs[p], label)+loss
p=p+1
total=total+1
print('Test Accuracy of the model on the 10000 test images: {} %'.format(100 * correct / total))
保存模型:
# 保存模型
torch.save(model.state_dict(), 'model.ckpt')
然后来看一下我们的测试结果:

下面是2.6的全部代码:
#coding=gbk
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
#定义超参数
num_epochs = 5
num_classes = 10
batch_size = 32
learning_rate = 0.001
# 设备配置
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
# MNIST 数据集
train_dataset = torchvision.datasets.MNIST(root='../../data/',
train=True,
transform=transforms.ToTensor(),
download=True)
test_dataset = torchvision.datasets.MNIST(root='../../data/',
train=False,
transform=transforms.ToTensor())
# 数据加载器
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
class Classifier(nn.Module):
def __init__(self):
# 初始化PyTorch父类
super().__init__()
# 定义神经网络层
self.model = nn.Sequential(
nn.Linear(784, 200),
nn.Sigmoid(),
nn.Linear(200, 10),
nn.Sigmoid()
)
# 创建损失函数
def forward(self, inputs):
# 直接运行模型
inputs=inputs.reshape(-1,784)
return self.model(inputs)
model = Classifier().to(device)
criterion=nn.MSELoss()
optimizer= torch.optim.SGD(model.parameters(), lr=0.01)
total_step = len(train_loader)
for epoch in range(num_epochs):
for i, (images, labels) in enumerate(train_loader):
images = images.to(device)
labels = labels.to(device)
# 前向传播
outputs = model(images)
# print(outputs)
loss=0
p=0
for j in labels:
label=torch.tensor([0,0,0,0,0,0,0,0,0,0])
label[j]=1
label=label.type(dtype=torch.float)
label = label.to(device)
# print(label)
loss = criterion(outputs[p], label)+loss
p=p+1
# 向后优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
# print(i)
if (i+1) % 100 == 0:
print ('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}'
.format(epoch+1, num_epochs, i+1, total_step, loss.item()))
# 测试模型
model.eval() # eval mode (batchnorm uses moving mean/variance instead of mini-batch mean/variance)
with torch.no_grad():
correct = 0
total = 0
for images, labels in test_loader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
loss=0
p=0
for j in labels:
label=torch.tensor([0,0,0,0,0,0,0,0,0,0])
label[j]=1
label=label.type(dtype=torch.float)
label = label.to(device)
if outputs[p].argmax()==label[j]:
correct=correct+1
# print(label)
loss = criterion(outputs[p], label)+loss
p=p+1
total=total+1
print('Test Accuracy of the model on the 10000 test images: {} %'.format(100 * correct / total))
# 保存模型
torch.save(model.state_dict(), 'model.ckpt')
2.7 RNN和LSTM实战
RNN模型之前介绍了,我们直接实战啊。
思路就是用minist数据集,尺寸28x28拆分成28个序列输出模型。
还是一样的,导入相关库,设置超参数,加载数据集:
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
# Hyper Parameters
EPOCH = 1 # train the training data n times, to save time, we just train 1 epoch
BATCH_SIZE = 64
TIME_STEP = 28 # rnn time step / image height
INPUT_SIZE = 28 # rnn input size / image width
LR = 0.01 # learning rate
DOWNLOAD_MNIST = True # set to True if haven't download the data
# Mnist digital dataset
train_data = torchvision.datasets.MNIST(
root='../../data/',
train=True, # this is training data
transform=transforms.ToTensor(), # Converts a PIL.Image or numpy.ndarray to
# torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
download=DOWNLOAD_MNIST, # download it if you don't have it
)
print(train_data.train_data.size()) # (60000, 28, 28)
print(train_data.train_labels.size()) # (60000)
# 加载训练数据集
train_loader = torch.utils.data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
# 加载测试数据集,选取2000个样本以加快测试速度
test_data = torchvision.datasets.MNIST(root='../../data/', train=False, transform=transforms.ToTensor())
test_x = test_data.test_data.type(torch.FloatTensor)[:2000]/255. # shape (2000, 28, 28) value in range(0,1)
test_y = test_data.test_labels.numpy()[:2000] # covert to numpy array
定义RNN模型:
class RNN(nn.Module):
def __init__(self):
super(RNN, self).__init__()
self.rnn = nn.LSTM( # if use nn.RNN(), it hardly learns
input_size=INPUT_SIZE,
hidden_size=64, # rnn hidden unit
num_layers=1, # number of rnn layer
batch_first=True, # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(64, 10)
def forward(self, x):
# x shape (batch, time_step, input_size)
# r_out shape (batch, time_step, output_size)
# h_n shape (n_layers, batch, hidden_size)
# h_c shape (n_layers, batch, hidden_size)
r_out, (h_n, h_c) = self.rnn(x, None) # None represents zero initial hidden state
# choose r_out at the last time step
out = self.out(r_out[:, -1, :])
return out
优化器和模型测试:
optimizer = torch.optim.Adam(rnn.parameters(), lr=LR)
loss_func = nn.CrossEntropyLoss()
# 训练
for epoch in range(EPOCH):
for step, (b_x, b_y) in enumerate(train_loader): # gives batch data
b_x = b_x.view(-1, 28, 28) # reshape x to (batch, time_step, input_size)
output = rnn(b_x) # rnn output
loss = loss_func(output, b_y) # cross entropy loss
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if step % 50 == 0:
test_output = rnn(test_x) # (samples, time_step, input_size)
pred_y = torch.max(test_output, 1)[1].data.numpy()
accuracy = float((pred_y == test_y).astype(int).sum()) / float(test_y.size)
print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)
# print 10 predictions from test data
test_output = rnn(test_x[:10].view(-1, 28, 28))
pred_y = torch.max(test_output, 1)[1].data.numpy()
print(pred_y, 'prediction number')
print(test_y[:10], 'real number')
效果:

模型效果还是挺厉害的:
模型代码实现如下:
class LSTM(nn.Module):
def __init__(self):
super(LSTM, self).__init__()
self.rnn = nn.LSTM( # if use nn.RNN(), it hardly learns
input_size=INPUT_SIZE,
hidden_size=64, # rnn hidden unit
num_layers=1, # number of rnn layer
batch_first=True, # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(64, 10)
def forward(self, x):
# x shape (batch, time_step, input_size)
# r_out shape (batch, time_step, output_size)
# h_n shape (n_layers, batch, hidden_size)
# h_c shape (n_layers, batch, hidden_size)
r_out, (h_n, h_c) = self.rnn(x, None) # None represents zero initial hidden state
# choose r_out at the last time step
out = self.out(r_out[:, -1, :])
return out
然后是LSTM实战,因为RNN和LSTM很像,所以,我们其他的不用动了,改模型那块代码就可以了。
lstm模型就厉害多了:
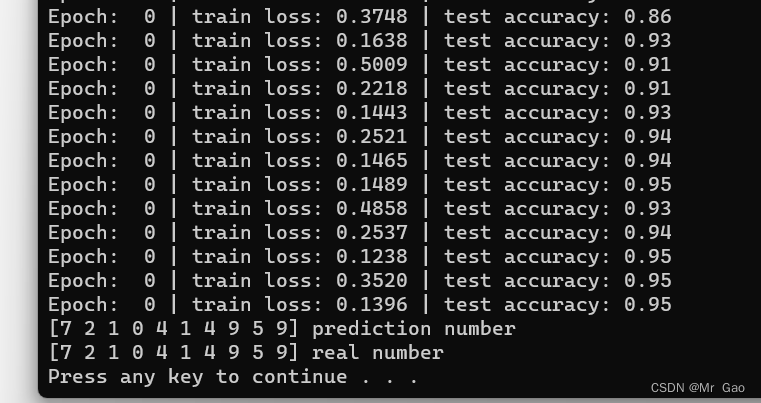
这一部分的完整代码如下:
#coding=gbk
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
# Hyper Parameters
EPOCH = 1 # train the training data n times, to save time, we just train 1 epoch
BATCH_SIZE = 64
TIME_STEP = 28 # rnn time step / image height
INPUT_SIZE = 28 # rnn input size / image width
LR = 0.01 # learning rate
DOWNLOAD_MNIST = True # set to True if haven't download the data
# Mnist digital dataset
train_data = torchvision.datasets.MNIST(
root='../../data/',
train=True, # this is training data
transform=transforms.ToTensor(), # Converts a PIL.Image or numpy.ndarray to
# torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
download=DOWNLOAD_MNIST, # download it if you don't have it
)
print(train_data.train_data.size()) # (60000, 28, 28)
print(train_data.train_labels.size()) # (60000)
# 加载训练数据集
train_loader = torch.utils.data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
# 加载测试数据集,选取2000个样本以加快测试速度
test_data = torchvision.datasets.MNIST(root='../../data/', train=False, transform=transforms.ToTensor())
test_x = test_data.test_data.type(torch.FloatTensor)[:2000]/255. # shape (2000, 28, 28) value in range(0,1)
test_y = test_data.test_labels.numpy()[:2000] # covert to numpy array
class RNN(nn.Module):
def __init__(self):
super(RNN, self).__init__()
self.rnn = nn.RNN( # if use nn.RNN(), it hardly learns
input_size=INPUT_SIZE,
hidden_size=28, # rnn hidden unit
num_layers=1, # number of rnn layer
batch_first=True, # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(28, 10)
def forward(self, x):
# x shape (batch, time_step, input_size)
# r_out shape (batch, time_step, output_size)
# h_n shape (n_layers, batch, hidden_size)
# h_c shape (n_layers, batch, hidden_size)
# print(self.rnn(x, None))
r_out,h = self.rnn(x, None) # None represents zero initial hidden state
# choose r_out at the last time step
out = self.out(r_out[:, -1, :])
return out
#print(rnn)
class LSTM(nn.Module):
def __init__(self):
super(LSTM, self).__init__()
self.rnn = nn.LSTM( # if use nn.RNN(), it hardly learns
input_size=INPUT_SIZE,
hidden_size=64, # rnn hidden unit
num_layers=1, # number of rnn layer
batch_first=True, # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(64, 10)
def forward(self, x):
# x shape (batch, time_step, input_size)
# r_out shape (batch, time_step, output_size)
# h_n shape (n_layers, batch, hidden_size)
# h_c shape (n_layers, batch, hidden_size)
r_out, (h_n, h_c) = self.rnn(x, None) # None represents zero initial hidden state
# choose r_out at the last time step
out = self.out(r_out[:, -1, :])
return out
rnn = LSTM()
#rnn = RNN()
optimizer = torch.optim.Adam(rnn.parameters(), lr=LR)
loss_func = nn.CrossEntropyLoss()
# 训练
for epoch in range(EPOCH):
for step, (b_x, b_y) in enumerate(train_loader): # gives batch data
b_x = b_x.view(-1, 28, 28) # reshape x to (batch, time_step, input_size)
output = rnn(b_x) # rnn output
# print(output)
loss = loss_func(output, b_y) # cross entropy loss
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if step % 50 == 0:
test_output = rnn(test_x) # (samples, time_step, input_size)
pred_y = torch.max(test_output, 1)[1].data.numpy()
accuracy = float((pred_y == test_y).astype(int).sum()) / float(test_y.size)
print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)
# print 10 predictions from test data
test_output = rnn(test_x[:10].view(-1, 28, 28))
pred_y = torch.max(test_output, 1)[1].data.numpy()
print(pred_y, 'prediction number')
print(test_y[:10], 'real number')
好的,到这里,这次教程就算是结束了,以后博主还是会继续更新这方面的内容的。有问题可以再博客下面留言。