写在前边

关于$cast转换的结论无外乎以下四条：

如果将子类句柄复制给父类句柄，可以实现父类句柄的向下转换，可以不使用$cast完成，属于一种静态的转换，如果类型不匹配会在编译时报错；
如果将父类句柄复制给子类句柄，可是实现子类句柄的向上转换，$cast在转换时需要检查要转换的两个句柄指向对象的类型，如果转换源类型与目的类型所指向对象的类型一致或者是目的类型指向的对象是源类型的父类，那么可以使用$cast进行转换。
对于类中的属性，SV会根据句柄handle本身的类型进行判定，父类句柄指访问的仍然是父类句柄类型中的属性；
$cast是作为任务还是作为函数使用，仿真时会根据使用的上下文决定具体调用的方式。

我相信以上的结论大家不止在一篇文章中见到，但是当自己使用cast的时候，嗯......，不是转换不成功就是会报类型不匹配的问题。后来发现，靠，我居然还是不会。不好意思，以上内容根据自己亲身经历演变而来。咱们言归正传，本文将主要针对以上结论中的红色字体内容进行深入剖析，解释。

1. what？又报错：

上来就是一个报错场景，这就是没有彻底理解以上结论造成的（如果转换源类型与目的类型所指向对象的类型一致或者是目的类型指向的对象是源类型的父类，那么可以使用$cast进行转换）；以下代码声明了一个父类father，一个继承于father的子类child1。按照最初的理解，目的类型指向的对象是源类型的父类，不就是下边的cast转换吗？但是，偏偏会报错，这是为什么呢？

class father;
	string m_name;
	
	function new(string name);
	m_name = name;
	endfunction
	
	function void print();
		$display("HELLOW %s",m_name);
	endfunction
endclass:father
 
class child1 extends father;
	string plane="plane";
	
	function new(string name);
	super.new(name);
	endfunction
endclass:child1
 
module top;
	father f;
	child1 c1;
	child1 c2;
	initial begin
		f=new("father");
		$cast(c2,f);
		f.print();
		$write(",has %s", c2.plane);
		end
endmodule:top

仿真结果：

报错信息是类型不匹配，究竟是什么原因导致的呢？

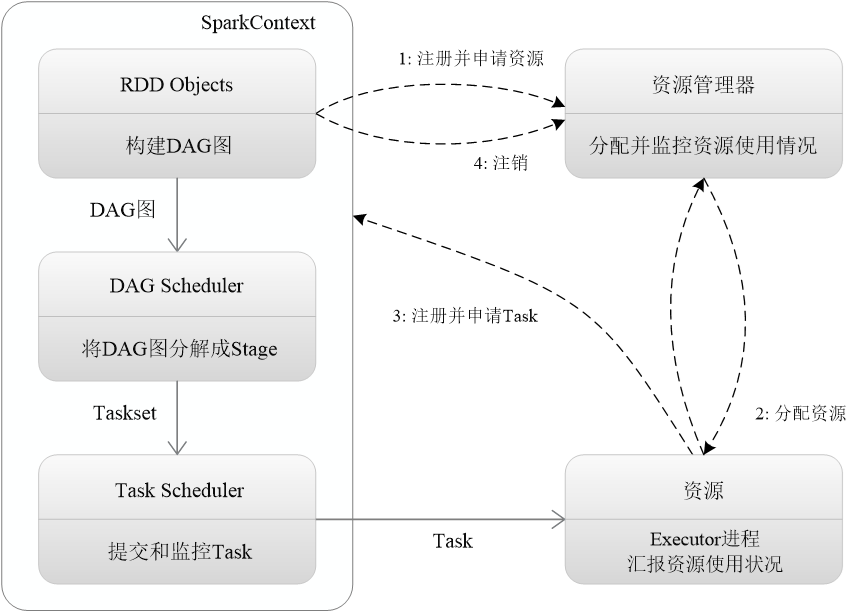
2. 靠，难道是这样？

请允许我将以上的继承关系画出来，这可能有助于我们找到答案。

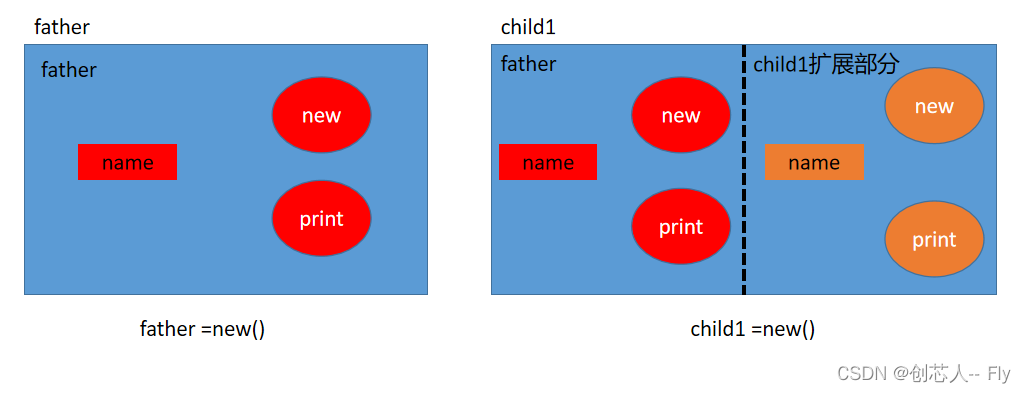
以上图片其实就想说明一个问题，father = new(),开辟的空间是左边的只有father的空间，但是child1=new()开辟的空间除了包含有child自身的(图上表示为child1拓展部分)，还有其父类father的部分。以上代码首先对father进行了实例化，开辟了空间，接着进行$cast(子类句柄，子类句柄的父类对象)转换，这是不被允许的。其实上边结论说的目的类型指向的对象是源类型的父类是可以进行cast转换的，指的是$cast(子类句柄，子类里边父类的对象(右边图的father部分)，而不是左边的father)。

3. 小试牛刀

class father;
	string m_name;
	bit    index = 0;
	function new(string name);
	m_name = name;
	endfunction
	
	function void print();
		$display(" 1 :HELLOW %s, index = %b",m_name, index);
	endfunction
endclass:father
 
 
class child1 extends father;
	string plane="plane";
	bit    index = 1;

	function new(string name);
	super.new(name);
	endfunction

    function void print();
		$display("2: HELLOW %s, index = %b",m_name, index);
	endfunction

endclass:child1
 
module top;
	father f;
	child1 c1;
	child1 c2;
	initial begin
		c1=new("child1");
		f=c1;
		f.print();
		c1.plane="big_plane";
		$cast(c2,f);
		f.print();
		$write(",has %s", c2.plane);
		end
endmodule:top

将原始代码进行了修改，主要在top部分，首先初始化子类，开辟空间，父类句柄指向子类对象，这是允许的。此时，父类指向的是子类空间中父类的那一部分空间，如打印结果所示。但是其所属的类型为子类。接下来进行cast转换就不存在上边的问题了。看了打印结果，心头一紧，真TMNB，这个理解就目前而言可以说服自己了。