翻筋斗觅食策略改进灰狼算法

news2024/9/21 16:38:18

一、动态扰动因子策略

二、翻筋斗觅食策略

三、改进灰狼算法收敛曲线图

灰狼优化算法(grey wolf optimization,GWO)存在收敛的不合理性等缺陷，目前对GWO算法的收敛性改进方式较少，除此之外，当GWO迭代至后期，所有灰狼个体都逼近 $\alpha$ 狼、 $\beta$ 狼、 $\delta$ 狼，导致算法陷入局部最优。针对以上问题，提出了一种增强型的灰狼优化算法IGWO。首先引入一种扰动因子，平衡了算法的开采和勘探能力;其次引入翻筋斗觅食策略，在后期使其不陷入局部最优的同时也使得前期的群体多样性略有提升。对IGWO算法的寻优性能进行验证，结果表明IGWO算法在寻优性能上较GWO算法有明显优势。

一、动态扰动因子策略

在原始GWO算法中，开采与勘探的过渡是由H决定的，也就是由收敛因子a决定。|H|>1时，狼群进行全局搜索，扩大勘探范围的同时增强其全局性;|H|<1时，狼群进行局部搜索，提高局部搜索效率。然而缺点是a的前半段与后半段下降幅度是相同的，导致无法在前期更好地全局搜索，而后期无法更有效地进行局部搜索，这在处理复杂优化问题时会显露弊端。大多数情况不能保证全局最优解在收敛的末端出现，会出现早熟收敛和后期陷入局部最优的情形。关于a的改进一般是变线性为非线性，使前期的a平稳过渡，增强全局勘探能力;后期a急速下降呈陡崖状，增强其局部开采能力。本文将引入新的动态扰动因子策略以确保精度，扰动因子E和更新后的H如式1所示。这里的H为灰狼算法中的A， $\rho _{1}$ 为灰狼算法中的 $r_{1}$ 。

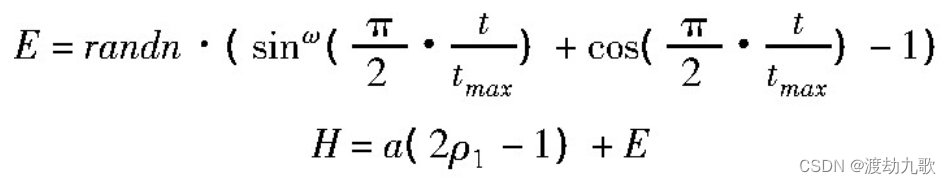
其中:randn代表服从高斯正态分布的随机数;ω代表某一常数，它决定了扰动因子峰值的位置。

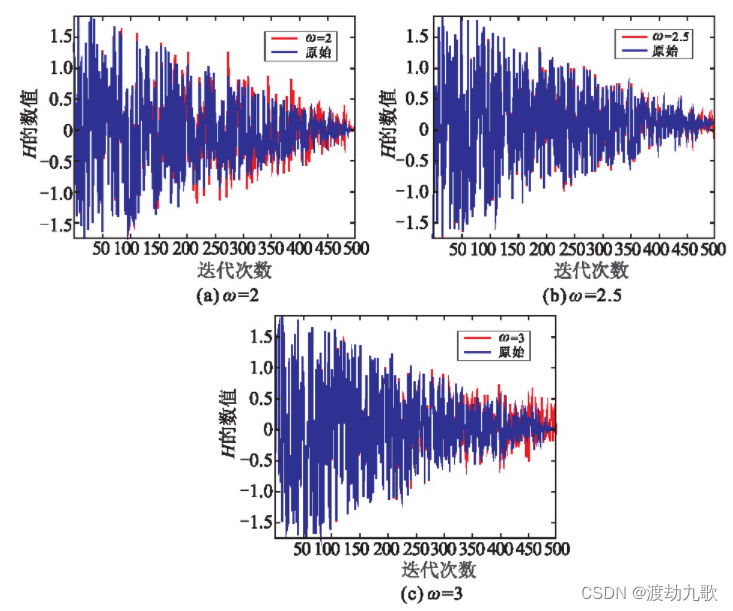
图1可以看出不同ω值的扰动因子振幅情况，振幅随着ω的增加而减小，最早出现较大振幅的是ω=2的扰动因子。

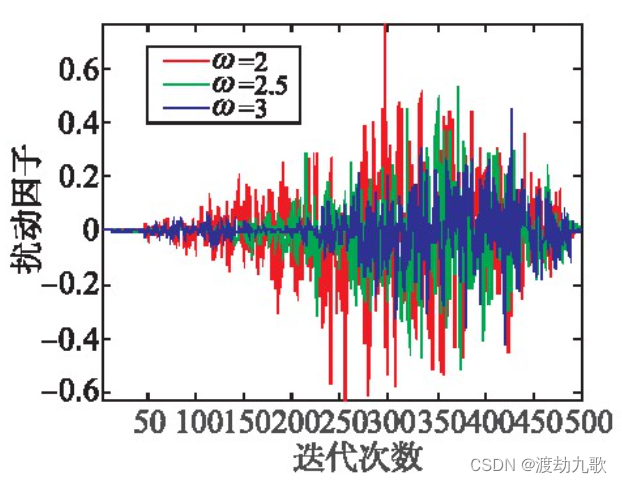
由于H值是位置更新的一部分，它不仅是全局和局部搜索转换的关键，而且还影响了算法的收敛性。具体来说，其数值越大、勘探越多，数值越小、开采越多。图 2 给出了随着迭代的更新H的变化。从图中可以看出，当ω=2时，|H|在迭代后期会突然大于1，且扰动因子的振幅较大，严重影响了收敛性；当ω=3时，扰动因子的振幅较小，后期跳出局部最优的能力会变弱，但是并不影响算法本身的性能；当ω=2.5时，可以看出收敛性略有提升。对比之下，若是优化一些包含局部最优的适应度函数，将ω设为3可能会降低精度，而将ω设为2，得到的结果与原算法相似，而将ω设为2.5可以提升算法的性能。

二、翻筋斗觅食策略

由于灰狼优化算法后期易陷入局部最优，通过蝠鲼觅食会突然翻身捕捉浮游生物，引入较为新颖的翻筋斗觅食策略来改善GWO算法跳出局部最优的能力。这种捕猎行为，可以将猎物视为一个支点，每次捕猎将会更新到当前位置与对称于支点对面位置的某一位置，数学模型如下:

其中: $S$ 代表空翻因子，决定了翻到猎物对面的位置，取 $S=2$ ； $x_{best}^{d}$ 为猎物位置； $N$ 为狼群数量； $d$ 为维度； $r_{1}$ 、 $r_{2}$ 为两个在[0,1]的随机数。灰狼翻筋斗觅食示意图如图3所示。

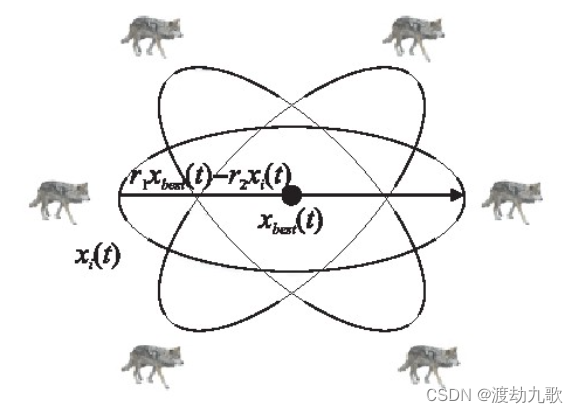
由图3可以看出，每一只灰狼移动的位置位于当前位置和对称于猎物位置的位置之间，在于寻求一个靠近最优解的更佳搜索域，随着个体位置与最优解之间的距离越来越小，当前位置的波动也会越来越小，最终每一只狼都将逼近最优解，搜索空间也会越来越小。因此，随着迭代次数的增加，翻筋斗觅食的范围也在自适应地减小。在每一次的迭代中，当前灰狼 $x_{i}^{d}(t)$ 会与其跳跃支点后的灰狼进行适应度对比，如果此时已经陷入局部最优，则灰狼 $x_{i}^{d}(t)$ 可能会被跳跃支点后的灰狼取代(取决于适应度值)，而随着迭代的进行，被取代的概率就越大，跳出局部最优的效果就越明显。与反向学习策略不同的是，翻筋斗策略在更新位置时是围绕最优狼进行的，这使得算法具有更强的收敛性。

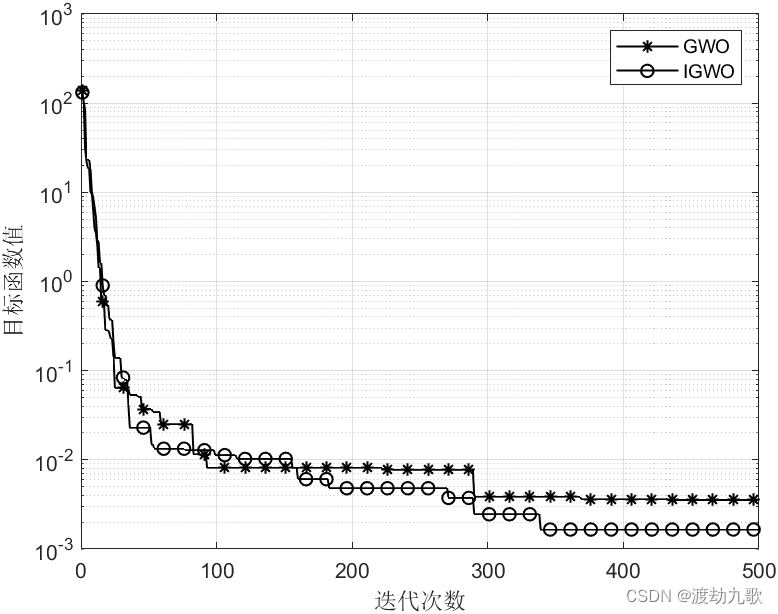
三、改进灰狼算法收敛曲线图

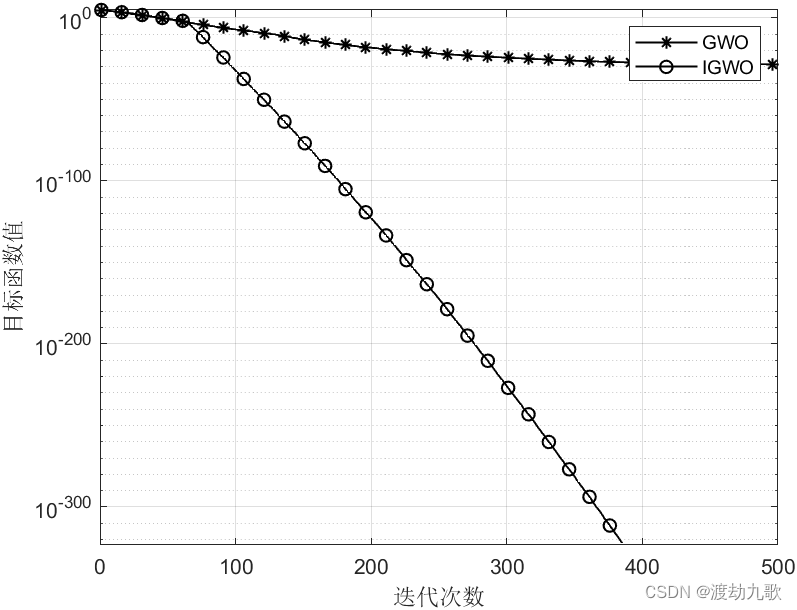
F1:

The best optimal value of the objective funciton found by GWO is : 3.061e-28
The best optimal value of the objective funciton found by IGWO is : 0

F7:

The best optimal value of the objective funciton found by GWO is : 0.0026498
The best optimal value of the objective funciton found by IGWO is : 0.0010795