永磁直线电机数学模型的建立,是进行后续控制仿真和实验的前提。为了实现永磁同步直线电机的矢量控制,需要把永磁同步直线电机假想成永磁同步旋转电机,借鉴旋转电机的电流分析方式,实现dq轴电流控制的解耦,并且把永磁同步直线电机的行波磁场假想为旋转的空间磁场。(都是三相磁场去合成,其实原理是一致的,位置信息只提供正弦波的相位)
进行如下假设:
- 忽略铁芯饱和;
- 不计涡流和磁滞损耗;
- 初级上没有阻尼绕组,永磁体也没有阻尼作用;
- 反电动势不受电感饱和作用干扰,仅表现为正弦;
取永磁体的基波磁场的水平方向为d轴,q 轴超前 d 轴90° 电角度。参考坐标系的旋转速度即为等效直线行进过程中的角速度。在上述假定下,以定子参考坐标系的数学模型:
(1)电压方程
先看一个熟悉的形式,如下所示,这个表达式与永磁同步电机完全一致,里面包含定子电阻压降、电感感应电压、耦合电压;
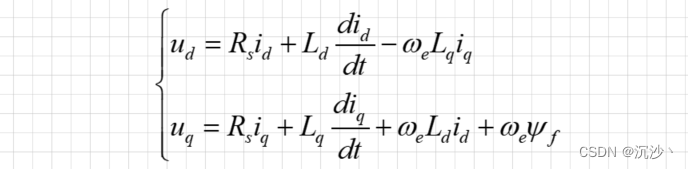
存在区别的地方就是电角速度 we 的表达式上,因为永磁直线同步电机的形成是直线的,不再是以旋转的形式进行运动,其速度在公式上的表现也应与其运行形式对应,直线电机中电角速度与直线运行动子速度之间的关系为:

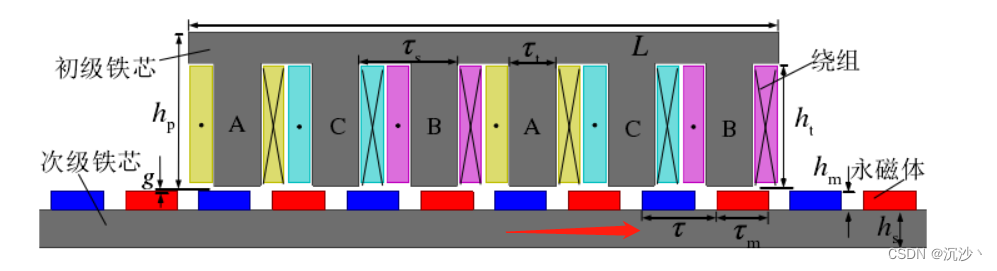
上式中极距 = 磁体长度 + 磁体间距,极对数动子下面包含的极对数,下图中动子下面盖住了8个极,所以极对数是4;而动子速度就是动子直线运动的速度,单位为m/s。
整理一下可得:
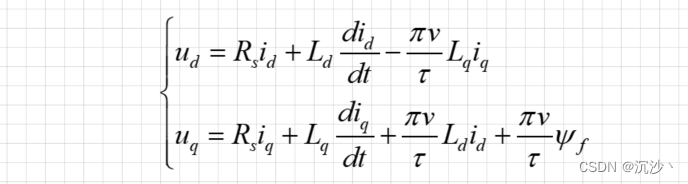
(2)磁链方程
磁链方程与永磁同步旋转电机完全一致;如下所示:
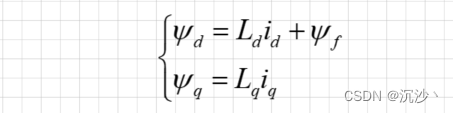
(3)运动方程
运动方程稍微特殊一些的地方在于:
- 质量 M 替代旋转的转动惯量 J;
- 极对数不再影响输出力矩大小,因为齿槽已被展开,影响力矩系数的是极距的大小;
- 多了端部效应力;
- 摩擦系数从旋转摩擦系数转变为滑动摩擦系数,该而滑动摩擦系数受到法向力的影响,由于端部效应会导致法向力的波动,所以端部效应除了会产生端部效应力,还会对摩擦力产生影响;