这篇博文主要分享ORB_SLAM3中Tracking::PreintegrateIMU(),其主要包括几个部分:
- 获得两帧之间的IMU数据
- 中值积分
- IMU状态更新
关于IMU的理论推导参考:
- ORB_SLAM3_IMU预积分理论推导(预积分项)
- ORB_SLAM3_IMU预积分理论推导(噪声分析)
- ORB_SLAM3_IMU预积分理论推导(更新)
- ORB_SLAM3_IMU预积分理论推导(残差)
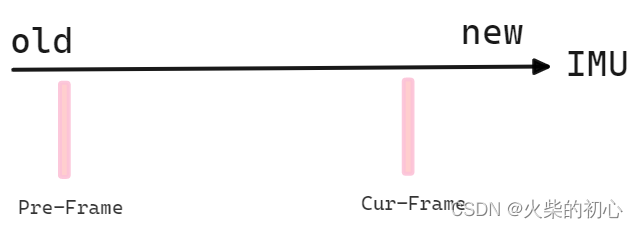
1.获得两帧之间的IMU数据
主要是为了获取当前帧和前一帧之间的IMU数据,以便用于后续的IMU预积分
while(true)
{
// 数据还没有时,会等待一段时间,直到mlQueueImuData中有imu数据.一开始不需要等待
bool bSleep = false;
{
unique_lock<mutex> lock(mMutexImuQueue);
if(!mlQueueImuData.empty())
{
// 拿到第一个imu数据作为起始数据
IMU::Point* m = &mlQueueImuData.front();
cout.precision(17);
// imu起始数据会比当前帧的前一帧时间戳早,如果相差0.001则舍弃这个imu数据
if(m->t<mCurrentFrame.mpPrevFrame->mTimeStamp-mImuPer)
{
mlQueueImuData.pop_front();
}
// 同样最后一个的imu数据时间戳也不能理当前帧时间间隔多余0.001
else if(m->t<mCurrentFrame.mTimeStamp-mImuPer)
{
mvImuFromLastFrame.push_back(*m);
mlQueueImuData.pop_front();
}
else
{
// 得到两帧间的imu数据放入mvImuFromLastFrame中,得到后面预积分的处理数据
mvImuFromLastFrame.push_back(*m);
break;
}
}
else
{
break;
bSleep = true;
}
}
if(bSleep)
usleep(500);
}
2.中值积分
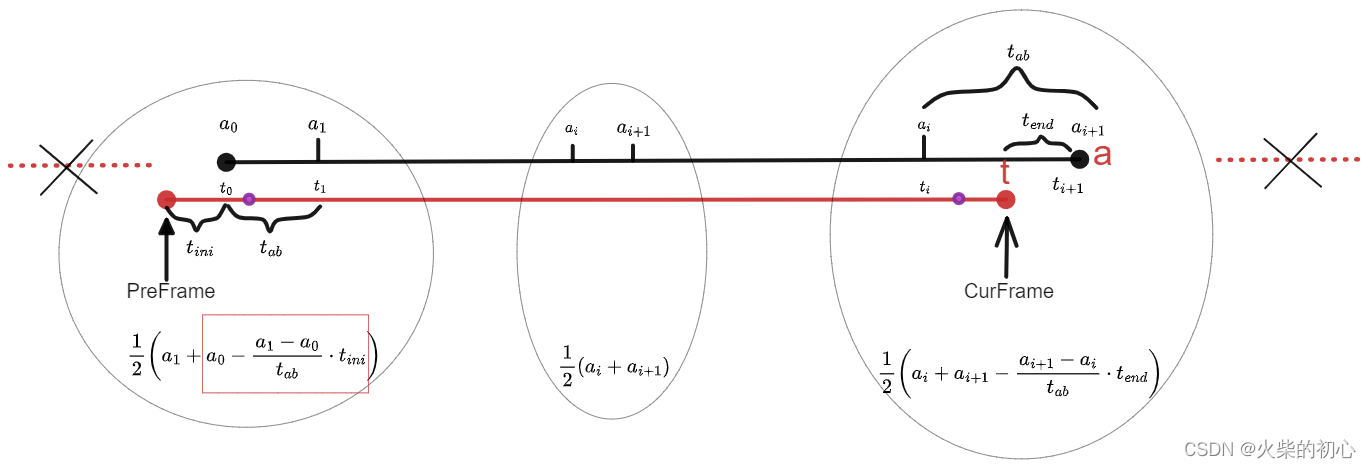
- 第一帧:线性插值得到
a
s
t
a
r
t
a_{start}
astart
1 2 ( a i + a i + 1 − a i + 1 − a i t a b ⋅ t i n i ) \frac{1}{2} \left (a_{i}+a_{i+1} - \frac{a_{i+1}-a_{i}}{t_{ab}}\cdot t_{ini} \right ) 21(ai+ai+1−tabai+1−ai⋅tini) - 中间帧
1 2 ( a i + a i + 1 ) \frac{1}{2} \left (a_{i}+a_{i+1} \right ) 21(ai+ai+1) - 最后帧:线性插值得到
a
e
n
d
a_{end}
aend
1 2 ( a i + a i + 1 − a i + 1 − a i t a b ⋅ t e n d ) \frac{1}{2} \left (a_{i}+a_{i+1} - \frac{a_{i+1}-a_{i}}{t_{ab}}\cdot t_{end} \right ) 21(ai+ai+1−tabai+1−ai⋅tend)
这里讲解下上述公式,以第一帧为例:
- 首先,线性插值得到
a
s
t
a
r
t
a_{start}
astart,也就是第一个红点处:
a 1 − a 0 t 1 − t 0 = a 0 − a t 0 − t ⇒ a = a 0 − a 1 − a 0 t 1 − t 0 ⋅ ( t 0 − t ) \begin{align} \frac{a_{1}-a_{0}}{t_{1}-t_{0}} & = \frac{a_{0}-a}{t_{0}-t} \\ \Rightarrow a & = a_{0} - \frac{a_{1}-a_{0}}{t_{1}-t_{0}} \cdot \left(t_{0}-t\right) \end{align} t1−t0a1−a0⇒a=t0−ta0−a=a0−t1−t0a1−a0⋅(t0−t) - 然后,取a与 a 1 a_{1} a1的平均值,得到
a 1 + a 0 − a 1 − a 0 t 1 − t 0 ⋅ ( t 0 − t ) a_{1} + a_{0} - \frac{a_{1}-a_{0}}{t_{1}-t_{0}} \cdot \left(t_{0}-t\right) a1+a0−t1−t0a1−a0⋅(t0−t)
IMU::Preintegrated* pImuPreintegratedFromLastFrame = new IMU::Preintegrated(mLastFrame.mImuBias,mCurrentFrame.mImuCalib);
// 针对预积分位置的不同做不同中值积分的处理
/**
* 根据上面imu帧的筛选,IMU与图像帧的时序如下:
* Frame---IMU0---IMU1---IMU2---IMU3---IMU4---------------IMUx---Frame---IMUx+1
* T_------T0-----T1-----T2-----T3-----T4-----------------Tx-----_T------Tx+1
* A_------A0-----A1-----A2-----A3-----A4-----------------Ax-----_T------Ax+1
* W_------W0-----W1-----W2-----W3-----W4-----------------Wx-----_T------Wx+1
* T_和_T分别表示上一图像帧和当前图像帧的时间戳,A(加速度数据),W(陀螺仪数据),同理
*/
for(int i=0; i<n; i++)
{
float tstep;
Eigen::Vector3f acc, angVel;
// 第一帧数据但不是最后两帧,imu总帧数大于2
if((i==0) && (i<(n-1)))
{
// 获取相邻两段imu的时间间隔
float tab = mvImuFromLastFrame[i+1].t-mvImuFromLastFrame[i].t;
// 获取当前imu到上一帧的时间间隔
float tini = mvImuFromLastFrame[i].t-mCurrentFrame.mpPrevFrame->mTimeStamp;
// 设当前时刻imu的加速度a0,下一时刻加速度a1,时间间隔tab 为t10,tini t0p
// 正常情况下时为了求上一帧到当前时刻imu的一个平均加速度,但是imu时间不会正好落在上一帧的时刻,需要做补偿,要求得a0时刻到上一帧这段时间加速度的改变量
// 有了这个改变量将其加到a0上之后就可以表示上一帧时的加速度了。其中a0 - (a1-a0)*(tini/tab) 为上一帧时刻的加速度再加上a1 之后除以2就为这段时间的加速度平均值
// 其中tstep表示a1到上一帧的时间间隔,a0 - (a1-a0)*(tini/tab)这个式子中tini可以是正也可以是负表示时间上的先后,(a1-a0)也是一样,多种情况下这个式子依然成立
acc = (mvImuFromLastFrame[i].a+mvImuFromLastFrame[i+1].a-
(mvImuFromLastFrame[i+1].a-mvImuFromLastFrame[i].a)*(tini/tab))*0.5f;
// 计算过程类似加速度
angVel = (mvImuFromLastFrame[i].w+mvImuFromLastFrame[i+1].w-
(mvImuFromLastFrame[i+1].w-mvImuFromLastFrame[i].w)*(tini/tab))*0.5f;
tstep = mvImuFromLastFrame[i+1].t-mCurrentFrame.mpPrevFrame->mTimeStamp;
}
else if(i<(n-1))
{
// 中间的数据不存在帧的干扰,正常计算
acc = (mvImuFromLastFrame[i].a+mvImuFromLastFrame[i+1].a)*0.5f;
angVel = (mvImuFromLastFrame[i].w+mvImuFromLastFrame[i+1].w)*0.5f;
tstep = mvImuFromLastFrame[i+1].t-mvImuFromLastFrame[i].t;
}
// 直到倒数第二个imu时刻时,计算过程跟第一时刻类似,都需要考虑帧与imu时刻的关系
else if((i>0) && (i==(n-1)))
{
float tab = mvImuFromLastFrame[i+1].t-mvImuFromLastFrame[i].t;
float tend = mvImuFromLastFrame[i+1].t-mCurrentFrame.mTimeStamp;
acc = (mvImuFromLastFrame[i].a+mvImuFromLastFrame[i+1].a-
(mvImuFromLastFrame[i+1].a-mvImuFromLastFrame[i].a)*(tend/tab))*0.5f;
angVel = (mvImuFromLastFrame[i].w+mvImuFromLastFrame[i+1].w-
(mvImuFromLastFrame[i+1].w-mvImuFromLastFrame[i].w)*(tend/tab))*0.5f;
tstep = mCurrentFrame.mTimeStamp-mvImuFromLastFrame[i].t;
}
// 就两个数据时使用第一个时刻的,这种情况应该没有吧,,回头应该试试看
else if((i==0) && (i==(n-1)))
{
acc = mvImuFromLastFrame[i].a;
angVel = mvImuFromLastFrame[i].w;
tstep = mCurrentFrame.mTimeStamp-mCurrentFrame.mpPrevFrame->mTimeStamp;
}
// Step 3.依次进行预积分计算
// 应该是必存在的吧,一个是相对上一关键帧,一个是相对上一帧
if (!mpImuPreintegratedFromLastKF)
cout << "mpImuPreintegratedFromLastKF does not exist" << endl;
mpImuPreintegratedFromLastKF->IntegrateNewMeasurement(acc,angVel,tstep);
pImuPreintegratedFromLastFrame->IntegrateNewMeasurement(acc,angVel,tstep);
}
3.IMU状态更新
在此过程中,视IMU的bias不变,更新的顺序如下,主要和每个变量相互之间的依赖关系有关,其依赖关系如图所示
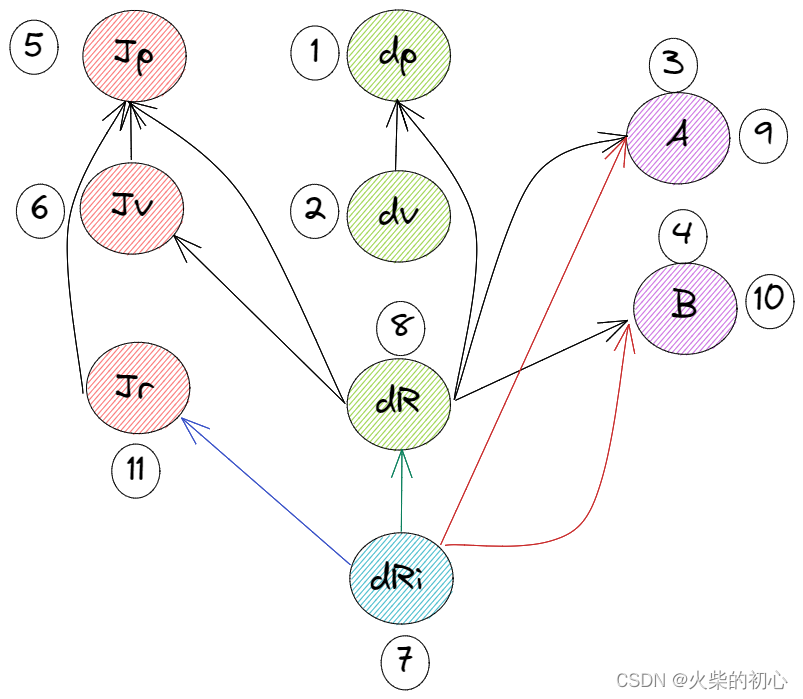
更新预积分测量值更新中的dP、dV
- dP包含上一次的dV和dR
- dV包含上一次的dR
Δ v ~ i j − 1 → Δ v ~ i j \Delta \tilde{v}_{ij-1} \to \Delta \tilde{v}_{ij} Δv~ij−1→Δv~ij
Δ v ~ i j ≜ ∑ k = i j − 1 [ Δ R ~ i k ⋅ ( f ~ k − b i a ) ⋅ Δ t ] ≜ ∑ k = i j − 2 [ Δ R ~ i k ⋅ ( f ~ k − b i a ) ⋅ Δ t ] + Δ R ~ i j − 1 ⋅ ( f ~ j − 1 − b i a ) ⋅ Δ t ≜ Δ v ~ i j − 1 + Δ R ~ i j − 1 ⋅ ( f ~ j − 1 − b i a ) ⋅ Δ t \begin{array}{l} \Delta \tilde{\mathbf{v}}_{i j} \triangleq \sum_{k=i}^{j-1}\left[\Delta \tilde{\mathbf{R}}_{i k} \cdot\left(\tilde{\mathbf{f}}_{k}-\mathbf{b}_{i}^{a}\right) \cdot \Delta t\right] \\ \triangleq \sum_{k=i}^{j-2}\left[\Delta \tilde{\mathbf{R}}_{i k} \cdot\left(\tilde{\mathbf{f}}_{k}-\mathbf{b}_{i}^{a}\right) \cdot \Delta t\right] + \Delta \tilde{\mathbf{R}}_{i j-1} \cdot\left(\tilde{\mathbf{f}}_{j-1}-\mathbf{b}_{i}^{a}\right) \cdot \Delta t\\ \triangleq \Delta \tilde{\mathbf{v}}_{i j-1}+ \Delta \tilde{\mathbf{R}}_{i j-1} \cdot\left(\tilde{\mathbf{f}}_{j-1}-\mathbf{b}_{i}^{a}\right) \cdot \Delta t \end{array} Δv~ij≜∑k=ij−1[ΔR~ik⋅(f~k−bia)⋅Δt]≜∑k=ij−2[ΔR~ik⋅(f~k−bia)⋅Δt]+ΔR~ij−1⋅(f~j−1−bia)⋅Δt≜Δv~ij−1+ΔR~ij−1⋅(f~j−1−bia)⋅Δt
Δ p ~ i j − 1 → Δ p ~ i j \Delta \tilde{p}_{ij-1} \to \Delta \tilde{p}_{ij} Δp~ij−1→Δp~ij
Δ p ~ i j ≜ ∑ k = i j − 1 [ Δ v ~ i k Δ t + 1 2 Δ R ~ i k ⋅ ( f ~ k − b i a ) Δ t 2 ] ≜ ∑ k = i j − 2 [ Δ v ~ i k Δ t + 1 2 Δ R ~ i k ⋅ ( f ~ k − b i a ) Δ t 2 ] + Δ v ~ i j − 1 Δ t + 1 2 Δ R ~ i j − 1 ⋅ ( f ~ j − 1 − b i a ) Δ t 2 ≜ Δ p ~ i j − 1 + Δ v ~ i j − 1 Δ t + 1 2 Δ R ~ i j − 1 ⋅ ( f ~ j − 1 − b i a ) Δ t 2 \begin{array}{l} \Delta \tilde{\mathbf{p}}_{i j} \triangleq \sum_{k = i}^{j-1}\left[\Delta \tilde{\mathbf{v}}_{i k} \Delta t+\frac{1}{2} \Delta \tilde{\mathbf{R}}_{i k} \cdot\left(\tilde{\mathbf{f}}_{k}-\mathbf{b}_{i}^{a}\right) \Delta t^{2}\right] \\ \triangleq \sum_{k = i}^{j-2}\left[\Delta \tilde{\mathbf{v}}_{i k} \Delta t+\frac{1}{2} \Delta \tilde{\mathbf{R}}_{i k} \cdot\left(\tilde{\mathbf{f}}_{k}-\mathbf{b}_{i}^{a}\right) \Delta t^{2}\right] + \Delta \tilde{\mathbf{v}}_{i j-1} \Delta t+\frac{1}{2} \Delta \tilde{\mathbf{R}}_{i j-1} \cdot\left(\tilde{\mathbf{f}}_{j-1}-\mathbf{b}_{i}^{a}\right) \Delta t^{2} \\ \triangleq \Delta \tilde{\mathbf{p}}_{i j-1} + \Delta \tilde{\mathbf{v}}_{i j-1} \Delta t+\frac{1}{2} \Delta \tilde{\mathbf{R}}_{i j-1} \cdot\left(\tilde{\mathbf{f}}_{j-1}-\mathbf{b}_{i}^{a}\right) \Delta t^{2} \end{array} Δp~ij≜∑k=ij−1[Δv~ikΔt+21ΔR~ik⋅(f~k−bia)Δt2]≜∑k=ij−2[Δv~ikΔt+21ΔR~ik⋅(f~k−bia)Δt2]+Δv~ij−1Δt+21ΔR~ij−1⋅(f~j−1−bia)Δt2≜Δp~ij−1+Δv~ij−1Δt+21ΔR~ij−1⋅(f~j−1−bia)Δt2
dP = dP + dV * dt + 0.5f * dR * acc * dt * dt;
dV = dV + dR * acc * dt;
更新噪声更新中的A、B,主要是与 Δ R ~ i j − 1 \Delta \tilde{\mathbf{R}}_{i j-1} ΔR~ij−1有关部分
η i j Δ = [ Δ R ~ j j − 1 0 0 − Δ R ~ i j − 1 ⋅ ( f ~ j − 1 − b i a ) ∧ Δ t I 0 − 1 2 Δ R ~ i j − 1 ⋅ ( f ~ j − 1 − b i a ) ∧ Δ t 2 Δ t I I ] ⏟ A j − 1 η i j − 1 Δ ⋯ + [ J r j − 1 Δ t 0 0 Δ R ~ i j − 1 Δ t 0 1 2 Δ R ~ i j − 1 Δ t 2 ] ⏟ B j − 1 [ ( η j − 1 g d ) T ( η j − 1 a d ) T ] ⏟ η j − 1 d \begin{aligned} \boldsymbol{\eta}_{i j}^{\Delta}= &{\underbrace{ {\left[\begin{array}{ccc} \Delta \tilde{\mathbf{R}}_{j j-1} & \mathbf{0} & \mathbf{0} \\ -\Delta \tilde{\mathbf{R}}_{i j-1} \cdot\left(\tilde{\mathbf{f}}_{j-1}-\mathbf{b}_{i}^{a}\right)^{\wedge} \Delta t & \mathbf{I} & \mathbf{0} \\ -\frac{1}{2} \Delta \tilde{\mathbf{R}}_{i j-1} \cdot\left(\tilde{\mathbf{f}}_{j-1}-\mathbf{b}_{i}^{a}\right)^{\wedge} \Delta t^{2} & \Delta t \mathbf{I} & \mathbf{I} \end{array}\right]}} _{A_{j-1} }\boldsymbol{\eta}_{i j-1}^{\Delta} \cdots } \\ & +\underbrace{\left[\begin{array}{cc} \mathbf{J}_{r}^{j-1} \Delta t & \mathbf{0} \\ \mathbf{0} & \Delta \tilde{\mathbf{R}}_{i j-1} \Delta t \\ \mathbf{0} & \frac{1}{2} \Delta \tilde{\mathbf{R}}_{i j-1} \Delta t^{2} \end{array}\right]}_{B_{j-1}}\underbrace{ \begin{bmatrix} \left(\eta_{j-1}^{gd}\right)^T\\ \left(\eta_{j-1}^{ad}\right)^T \end{bmatrix} } _{\boldsymbol{\eta}_{j-1}^{d}} \end{aligned} ηijΔ=Aj−1 ΔR~jj−1−ΔR~ij−1⋅(f~j−1−bia)∧Δt−21ΔR~ij−1⋅(f~j−1−bia)∧Δt20IΔtI00I ηij−1Δ⋯+Bj−1 Jrj−1Δt000ΔR~ij−1Δt21ΔR~ij−1Δt2 ηj−1d (ηj−1gd)T(ηj−1ad)T
Eigen::Matrix<float, 3, 3> Wacc = Sophus::SO3f::hat(acc);
A.block<3, 3>(3, 0) = -dR * dt * Wacc;
A.block<3, 3>(6, 0) = -0.5f * dR * dt * dt * Wacc;
A.block<3, 3>(6, 3) = Eigen::DiagonalMatrix<float, 3>(dt, dt, dt);
B.block<3, 3>(3, 3) = dR * dt;
B.block<3, 3>(6, 3) = 0.5f * dR * dt * dt;
更新Jacobian更新中的JPa、JPg、JVa、JVg
-
∂
Δ
v
‾
i
j
−
1
∂
b
‾
g
→
∂
Δ
v
‾
i
j
∂
b
‾
g
\frac{\partial \Delta \overline{\mathbf{v}}_{i j-1}}{\partial \overline{\mathbf{b}}^{g}} \to \frac{\partial \Delta \overline{\mathbf{v}}_{i j}}{\partial \overline{\mathbf{b}}^{g}}
∂bg∂Δvij−1→∂bg∂Δvij
∂ Δ v ‾ i j ∂ b ‾ g = − ∑ k = i j − 1 ( Δ R ‾ i k ⋅ ( f ~ k − b ‾ i a ) ∧ ∂ Δ R ‾ i k ∂ b ‾ g Δ t ) = − ∑ k = i j − 2 ( Δ R ‾ i k ⋅ ( f ~ k − b ‾ i a ) ∧ ∂ Δ R ‾ i k ∂ b ‾ g Δ t ) − Δ R ‾ i j − 1 ⋅ ( f ~ j − 1 − b ‾ i a ) ∧ ∂ Δ R ‾ i j − 1 ∂ b ‾ g Δ t = ∂ Δ v ‾ i j − 1 ∂ b ‾ g − Δ R ‾ i j − 1 ⋅ ( f ~ j − 1 − b ‾ i a ) ∧ ∂ Δ R ‾ i j − 1 ∂ b ‾ g Δ t \begin{array}{l} \frac{\partial \Delta \overline{\mathbf{v}}_{i j}}{\partial \overline{\mathbf{b}}^{g}} =-\sum_{k=i}^{j-1}\left(\Delta \overline{\mathbf{R}}_{i k} \cdot\left(\tilde{\mathbf{f}}_{k}-\overline{\mathbf{b}}_{i}^{a}\right)^{\wedge} \frac{\partial \Delta \overline{\mathbf{R}}_{i k}}{\partial \overline{\mathbf{b}}^{g}} \Delta t\right) \\ =-\sum_{k=i}^{j-2}\left(\Delta \overline{\mathbf{R}}_{i k} \cdot\left(\tilde{\mathbf{f}}_{k}-\overline{\mathbf{b}}_{i}^{a}\right)^{\wedge} \frac{\partial \Delta \overline{\mathbf{R}}_{i k}}{\partial \overline{\mathbf{b}}^{g}} \Delta t\right) - \Delta \overline{\mathbf{R}}_{i j-1} \cdot\left(\tilde{\mathbf{f}}_{j-1}-\overline{\mathbf{b}}_{i}^{a}\right)^{\wedge} \frac{\partial \Delta \overline{\mathbf{R}}_{i j-1}}{\partial \overline{\mathbf{b}}^{g}} \Delta t \\ = \frac{\partial \Delta \overline{\mathbf{v}}_{i j-1}}{\partial \overline{\mathbf{b}}^{g}}-{\color{Green} \Delta \overline{\mathbf{R}}_{i j-1}} \cdot\left(\tilde{\mathbf{f}}_{j-1}-\overline{\mathbf{b}}_{i}^{a}\right)^{\wedge} {\color{Purple} \frac{\partial \Delta \overline{\mathbf{R}}_{i j-1}}{\partial \overline{\mathbf{b}}^{g}}} \Delta t \end{array} ∂bg∂Δvij=−∑k=ij−1(ΔRik⋅(f~k−bia)∧∂bg∂ΔRikΔt)=−∑k=ij−2(ΔRik⋅(f~k−bia)∧∂bg∂ΔRikΔt)−ΔRij−1⋅(f~j−1−bia)∧∂bg∂ΔRij−1Δt=∂bg∂Δvij−1−ΔRij−1⋅(f~j−1−bia)∧∂bg∂ΔRij−1Δt - ∂ Δ v ‾ i j − 1 ∂ b ‾ a → ∂ Δ v ‾ i j ∂ b ‾ a \frac{\partial \Delta \overline{\mathbf{v}}_{i j-1}}{\partial \overline{\mathbf{b}}^{a}} \to \frac{\partial \Delta \overline{\mathbf{v}}_{i j}}{\partial \overline{\mathbf{b}}^{a}} ∂ba∂Δvij−1→∂ba∂Δvij
∂ Δ v ‾ i j ∂ b ‾ a = − ∑ k = i j − 1 ( Δ R ‾ i k Δ t ) = − ∑ k = i j − 2 ( Δ R ‾ i k Δ t ) − Δ R ‾ i j − 1 Δ t = ∂ Δ v ‾ i j − 1 ∂ b ‾ a − Δ R ‾ i j − 1 Δ t \begin{array}{l} \frac{\partial \Delta \overline{\mathbf{v}}_{i j}}{\partial \overline{\mathbf{b}}^{a}} =-\sum_{k=i}^{j-1}\left(\Delta \overline{\mathbf{R}}_{i k} \Delta t\right) \\ =-\sum_{k=i}^{j-2}\left(\Delta \overline{\mathbf{R}}_{i k} \Delta t\right)-\Delta \overline{\mathbf{R}}_{i j-1} \Delta t \\ =\frac{\partial \Delta \overline{\mathbf{v}}_{i j-1}}{\partial \overline{\mathbf{b}}^{a}} -{\color{Green} \Delta \overline{\mathbf{R}}_{i j-1} } \Delta t \end{array} ∂ba∂Δvij=−∑k=ij−1(ΔRikΔt)=−∑k=ij−2(ΔRikΔt)−ΔRij−1Δt=∂ba∂Δvij−1−ΔRij−1Δt
- ∂ Δ p ‾ i j − 1 ∂ b ‾ g → ∂ Δ p ‾ i j ∂ b ‾ g \frac{\partial \Delta \overline{\mathbf{p}}_{i j-1}}{\partial \overline{\mathbf{b}}^{g}} \to \frac{\partial \Delta \overline{\mathbf{p}}_{i j}}{\partial \overline{\mathbf{b}}^{g}} ∂bg∂Δpij−1→∂bg∂Δpij
∂ Δ p ‾ i j ∂ b ‾ g = ∑ k = i j − 1 [ ∂ Δ v ‾ i k ∂ b ‾ g Δ t − 1 2 Δ R ‾ i k ⋅ ( f ~ k − b ‾ i a ) ∧ ∂ Δ R ‾ i k ∂ b ‾ g Δ t 2 ] = ∑ k = i j − 2 [ ∂ Δ v ‾ i k ∂ b ‾ g Δ t − 1 2 Δ R ‾ i k ⋅ ( f ~ k − b ‾ i a ) ∧ ∂ Δ R ‾ i k ∂ b ‾ g Δ t 2 ] + ∂ Δ v ‾ i j − 1 ∂ b ‾ g Δ t − 1 2 Δ R ‾ i j − 1 ⋅ ( f ~ j − 1 − b ‾ i a ) ∧ ∂ Δ R ‾ i j − 1 ∂ b ‾ g Δ t 2 = ∂ Δ p ‾ i j − 1 ∂ b ‾ g + ∂ Δ v ‾ i j − 1 ∂ b ‾ g Δ t − 1 2 Δ R ‾ i j − 1 ⋅ ( f ~ j − 1 − b ‾ i a ) ∧ ∂ Δ R ‾ i j − 1 ∂ b ‾ g Δ t 2 \begin{array}{l} \frac{\partial \Delta \overline{\mathbf{p}}_{i j}}{\partial \overline{\mathbf{b}}^{g}} =\sum_{k=i}^{j-1}\left[\frac{\partial \Delta \overline{\mathbf{v}}_{i k}}{\partial \overline{\mathbf{b}}^{g}} \Delta t-\frac{1}{2} \Delta \overline{\mathbf{R}}_{i k} \cdot\left(\tilde{\mathbf{f}}_{k}-\overline{\mathbf{b}}_{i}^{a}\right)^{\wedge} \frac{\partial \Delta \overline{\mathbf{R}}_{i k}}{\partial \overline{\mathbf{b}}^{g}} \Delta t^{2}\right] \\ =\sum_{k=i}^{j-2}\left[\frac{\partial \Delta \overline{\mathbf{v}}_{i k}}{\partial \overline{\mathbf{b}}^{g}} \Delta t-\frac{1}{2} \Delta \overline{\mathbf{R}}_{i k} \cdot\left(\tilde{\mathbf{f}}_{k}-\overline{\mathbf{b}}_{i}^{a}\right)^{\wedge} \frac{\partial \Delta \overline{\mathbf{R}}_{i k}}{\partial \overline{\mathbf{b}}^{g}} \Delta t^{2}\right] + {\color{Red} \frac{\partial \Delta \overline{\mathbf{v}}_{i j-1}}{\partial \overline{\mathbf{b}}^{g}}} \Delta t-\frac{1}{2} {\color{Green} \Delta \overline{\mathbf{R}}_{i j-1}} \cdot\left(\tilde{\mathbf{f}}_{j-1}-\overline{\mathbf{b}}_{i}^{a}\right)^{\wedge} {\color{Purple} \frac{\partial \Delta \overline{\mathbf{R}}_{i j-1}}{\partial \overline{\mathbf{b}}^{g}} } \Delta t^{2} \\ =\frac{\partial \Delta \overline{\mathbf{p}}_{i j-1}}{\partial \overline{\mathbf{b}}^{g}} + {\color{Red} \frac{\partial \Delta \overline{\mathbf{v}}_{i j-1}}{\partial \overline{\mathbf{b}}^{g}}} \Delta t-\frac{1}{2} {\color{Green} \Delta \overline{\mathbf{R}}_{i j-1}} \cdot\left(\tilde{\mathbf{f}}_{j-1}-\overline{\mathbf{b}}_{i}^{a}\right)^{\wedge} {\color{Purple} \frac{\partial \Delta \overline{\mathbf{R}}_{i j-1}}{\partial \overline{\mathbf{b}}^{g}} } \Delta t^{2} \end{array} ∂bg∂Δpij=∑k=ij−1[∂bg∂ΔvikΔt−21ΔRik⋅(f~k−bia)∧∂bg∂ΔRikΔt2]=∑k=ij−2[∂bg∂ΔvikΔt−21ΔRik⋅(f~k−bia)∧∂bg∂ΔRikΔt2]+∂bg∂Δvij−1Δt−21ΔRij−1⋅(f~j−1−bia)∧∂bg∂ΔRij−1Δt2=∂bg∂Δpij−1+∂bg∂Δvij−1Δt−21ΔRij−1⋅(f~j−1−bia)∧∂bg∂ΔRij−1Δt2
- ∂ Δ p ‾ i j − 1 ∂ b ‾ a → ∂ Δ p ‾ i j ∂ b ‾ a \frac{\partial \Delta \overline{\mathbf{p}}_{i j-1}}{\partial \overline{\mathbf{b}}^{a}} \to \frac{\partial \Delta \overline{\mathbf{p}}_{i j}}{\partial \overline{\mathbf{b}}^{a}} ∂ba∂Δpij−1→∂ba∂Δpij
∂ Δ p ‾ i j ∂ b ‾ a = ∑ k = i j − 1 [ ∂ Δ v ‾ i k ∂ b ‾ a Δ t − 1 2 Δ R ‾ i k Δ t 2 ] = ∑ k = i j − 2 [ ∂ Δ v ‾ i k ∂ b ‾ a Δ t − 1 2 Δ R ‾ i k Δ t 2 ] + ∂ Δ v ‾ i j − 1 ∂ b ‾ a Δ t − 1 2 Δ R ‾ i j − 1 Δ t 2 = ∂ Δ p ‾ i j − 1 ∂ b ‾ a + ∂ Δ v ‾ i j − 1 ∂ b ‾ a Δ t − 1 2 Δ R ‾ i j − 1 Δ t 2 \begin{array}{l} \frac{\partial \Delta \overline{\mathbf{p}}_{i j}}{\partial \overline{\mathbf{b}}^{a}} =\sum_{k=i}^{j-1}\left[\frac{\partial \Delta \overline{\mathbf{v}}_{i k}}{\partial \overline{\mathbf{b}}^{a}} \Delta t-\frac{1}{2} \Delta \overline{\mathbf{R}}_{i k} \Delta t^{2}\right] \\ =\sum_{k=i}^{j-2}\left[\frac{\partial \Delta \overline{\mathbf{v}}_{i k}}{\partial \overline{\mathbf{b}}^{a}} \Delta t-\frac{1}{2} \Delta \overline{\mathbf{R}}_{i k} \Delta t^{2}\right] + {\color{Red} \frac{\partial \Delta \overline{\mathbf{v}}_{i j-1}}{\partial \overline{\mathbf{b}}^{a}}} \Delta t-\frac{1}{2} {\color{Green} \Delta \overline{\mathbf{R}}_{i j-1} } \Delta t^{2} \\ =\frac{\partial \Delta \overline{\mathbf{p}}_{i j-1}}{\partial \overline{\mathbf{b}}^{a}} + {\color{Red} \frac{\partial \Delta \overline{\mathbf{v}}_{i j-1}}{\partial \overline{\mathbf{b}}^{a}}} \Delta t-\frac{1}{2} {\color{Green} \Delta \overline{\mathbf{R}}_{i j-1} } \Delta t^{2} \end{array} ∂ba∂Δpij=∑k=ij−1[∂ba∂ΔvikΔt−21ΔRikΔt2]=∑k=ij−2[∂ba∂ΔvikΔt−21ΔRikΔt2]+∂ba∂Δvij−1Δt−21ΔRij−1Δt2=∂ba∂Δpij−1+∂ba∂Δvij−1Δt−21ΔRij−1Δt2
JPa = JPa + JVa * dt - 0.5f * dR * dt * dt;
JPg = JPg + JVg * dt - 0.5f * dR * dt * dt * Wacc * JRg;
JVa = JVa - dR * dt;
JVg = JVg - dR * dt * Wacc * JRg;
更新dRi
由罗德里格公式计算 Δ R ~ j − 1 j \Delta \tilde{R} _{j-1j} ΔR~j−1j
IntegratedRotation::IntegratedRotation(const Eigen::Vector3f &angVel, const Bias &imuBias, const float &time)
{
// 得到考虑偏置后的角度旋转
const float x = (angVel(0) - imuBias.bwx) * time;
const float y = (angVel(1) - imuBias.bwy) * time;
const float z = (angVel(2) - imuBias.bwz) * time;
// 计算旋转矩阵的模值,后面用罗德里格公式计算旋转矩阵时会用到
const float d2 = x * x + y * y + z * z;
const float d = sqrt(d2);
Eigen::Vector3f v;
v << x, y, z;
// 角度转成叉积的矩阵形式
Eigen::Matrix3f W = Sophus::SO3f::hat(v);
// eps = 1e-4 是一个小量,根据罗德里格斯公式求极限,后面的高阶小量忽略掉得到此式
if (d < eps)
{
deltaR = Eigen::Matrix3f::Identity() + W;
rightJ = Eigen::Matrix3f::Identity();
}
else
{
deltaR = Eigen::Matrix3f::Identity() + W * sin(d) / d + W * W * (1.0f - cos(d)) / d2;
rightJ = Eigen::Matrix3f::Identity() - W * (1.0f - cos(d)) / d2 + W * W * (d - sin(d)) / (d2 * d);
}
}
更新预积分测量值更新中的dR
-
Δ
R
~
i
j
−
1
→
Δ
R
~
i
j
\Delta \tilde{R} _{ij-1}\to \Delta \tilde{R}_{ij}
ΔR~ij−1→ΔR~ij
Δ R ~ i j = ∏ k = i j − 1 Exp ( ( ω ~ k − b i g ) Δ t ) = ∏ k = i j − 2 Exp ( ( ω ~ k − b i g ) Δ t ) ⋅ Exp ( ( ω ~ j − 1 − b i g ) Δ t ) = Δ R ~ i j − 1 ⋅ Δ R ~ j − 1 j \begin{array}{l} \Delta \tilde{\mathbf{R}}_{i j}=\prod_{k=i}^{j-1} \operatorname{Exp}\left(\left(\tilde{\boldsymbol{\omega}}_{k}-\mathbf{b}_{i}^{g}\right) \Delta t\right) \\ =\prod_{k=i}^{j-2} \operatorname{Exp}\left(\left(\tilde{\boldsymbol{\omega}}_{k}-\mathbf{b}_{i}^{g}\right) \Delta t\right)\cdot \operatorname{Exp}\left(\left(\tilde{\boldsymbol{\omega}}_{j-1}-\mathbf{b}_{i}^{g}\right) \Delta t\right) \\ =\Delta \tilde{\mathbf{R}}_{i j-1}\cdot\Delta \tilde{\mathbf{R}}_{j-1 j} \end{array} ΔR~ij=∏k=ij−1Exp((ω~k−big)Δt)=∏k=ij−2Exp((ω~k−big)Δt)⋅Exp((ω~j−1−big)Δt)=ΔR~ij−1⋅ΔR~j−1j
dR = NormalizeRotation(dR * dRi.deltaR);
更新噪声更新中的A、B
η i j Δ = [ Δ R ~ j j − 1 0 0 − Δ R ~ i j − 1 ⋅ ( f ~ j − 1 − b i a ) ∧ Δ t I 0 − 1 2 Δ R ~ i j − 1 ⋅ ( f ~ j − 1 − b i a ) ∧ Δ t 2 Δ t I I ] ⏟ A j − 1 η i j − 1 Δ ⋯ + [ J r j − 1 Δ t 0 0 Δ R ~ i j − 1 Δ t 0 1 2 Δ R ~ i j − 1 Δ t 2 ] ⏟ B j − 1 [ ( η j − 1 g d ) T ( η j − 1 a d ) T ] ⏟ η j − 1 d \begin{aligned} \boldsymbol{\eta}_{i j}^{\Delta}= &{\underbrace{ {\left[\begin{array}{ccc} \Delta \tilde{\mathbf{R}}_{j j-1} & \mathbf{0} & \mathbf{0} \\ -\Delta \tilde{\mathbf{R}}_{i j-1} \cdot\left(\tilde{\mathbf{f}}_{j-1}-\mathbf{b}_{i}^{a}\right)^{\wedge} \Delta t & \mathbf{I} & \mathbf{0} \\ -\frac{1}{2} \Delta \tilde{\mathbf{R}}_{i j-1} \cdot\left(\tilde{\mathbf{f}}_{j-1}-\mathbf{b}_{i}^{a}\right)^{\wedge} \Delta t^{2} & \Delta t \mathbf{I} & \mathbf{I} \end{array}\right]}} _{A_{j-1} }\boldsymbol{\eta}_{i j-1}^{\Delta} \cdots } \\ & +\underbrace{\left[\begin{array}{cc} \mathbf{J}_{r}^{j-1} \Delta t & \mathbf{0} \\ \mathbf{0} & \Delta \tilde{\mathbf{R}}_{i j-1} \Delta t \\ \mathbf{0} & \frac{1}{2} \Delta \tilde{\mathbf{R}}_{i j-1} \Delta t^{2} \end{array}\right]}_{B_{j-1}}\underbrace{ \begin{bmatrix} \left(\eta_{j-1}^{gd}\right)^T\\ \left(\eta_{j-1}^{ad}\right)^T \end{bmatrix} } _{\boldsymbol{\eta}_{j-1}^{d}} \end{aligned} ηijΔ=Aj−1 ΔR~jj−1−ΔR~ij−1⋅(f~j−1−bia)∧Δt−21ΔR~ij−1⋅(f~j−1−bia)∧Δt20IΔtI00I ηij−1Δ⋯+Bj−1 Jrj−1Δt000ΔR~ij−1Δt21ΔR~ij−1Δt2 ηj−1d (ηj−1gd)T(ηj−1ad)T
A.block<3, 3>(0, 0) = dRi.deltaR.transpose();
B.block<3, 3>(0, 0) = dRi.rightJ * dt;
更新Jacobian更新中的JRg
- ∂ Δ p ‾ i j − 1 ∂ b ‾ a → ∂ Δ p ‾ i j ∂ b ‾ a \frac{\partial \Delta \overline{\mathbf{p}}_{i j-1}}{\partial \overline{\mathbf{b}}^{a}} \to \frac{\partial \Delta \overline{\mathbf{p}}_{i j}}{\partial \overline{\mathbf{b}}^{a}} ∂ba∂Δpij−1→∂ba∂Δpij
∂ Δ p ‾ i j ∂ b ‾ a = ∑ k = i j − 1 [ ∂ Δ v ‾ i k ∂ b ‾ a Δ t − 1 2 Δ R ‾ i k Δ t 2 ] = ∑ k = i j − 2 [ ∂ Δ v ‾ i k ∂ b ‾ a Δ t − 1 2 Δ R ‾ i k Δ t 2 ] + ∂ Δ v ‾ i j − 1 ∂ b ‾ a Δ t − 1 2 Δ R ‾ i j − 1 Δ t 2 = ∂ Δ p ‾ i j − 1 ∂ b ‾ a + ∂ Δ v ‾ i j − 1 ∂ b ‾ a Δ t − 1 2 Δ R ‾ i j − 1 Δ t 2 \begin{array}{l} \frac{\partial \Delta \overline{\mathbf{p}}_{i j}}{\partial \overline{\mathbf{b}}^{a}} =\sum_{k=i}^{j-1}\left[\frac{\partial \Delta \overline{\mathbf{v}}_{i k}}{\partial \overline{\mathbf{b}}^{a}} \Delta t-\frac{1}{2} \Delta \overline{\mathbf{R}}_{i k} \Delta t^{2}\right] \\ =\sum_{k=i}^{j-2}\left[\frac{\partial \Delta \overline{\mathbf{v}}_{i k}}{\partial \overline{\mathbf{b}}^{a}} \Delta t-\frac{1}{2} \Delta \overline{\mathbf{R}}_{i k} \Delta t^{2}\right] + {\color{Red} \frac{\partial \Delta \overline{\mathbf{v}}_{i j-1}}{\partial \overline{\mathbf{b}}^{a}}} \Delta t-\frac{1}{2} {\color{Green} \Delta \overline{\mathbf{R}}_{i j-1} } \Delta t^{2} \\ =\frac{\partial \Delta \overline{\mathbf{p}}_{i j-1}}{\partial \overline{\mathbf{b}}^{a}} + {\color{Red} \frac{\partial \Delta \overline{\mathbf{v}}_{i j-1}}{\partial \overline{\mathbf{b}}^{a}}} \Delta t-\frac{1}{2} {\color{Green} \Delta \overline{\mathbf{R}}_{i j-1} } \Delta t^{2} \end{array} ∂ba∂Δpij=∑k=ij−1[∂ba∂ΔvikΔt−21ΔRikΔt2]=∑k=ij−2[∂ba∂ΔvikΔt−21ΔRikΔt2]+∂ba∂Δvij−1Δt−21ΔRij−1Δt2=∂ba∂Δpij−1+∂ba∂Δvij−1Δt−21ΔRij−1Δt2
- ∂ Δ R ‾ i j − 1 ∂ b ‾ g → ∂ Δ R ‾ i j ∂ b ‾ g \frac{\partial \Delta \overline{\mathbf{R}}_{i j-1}}{\partial \overline{\mathbf{b}}^{g}} \to \frac{\partial \Delta \overline{\mathbf{R}}_{i j}}{\partial \overline{\mathbf{b}}^{g}} ∂bg∂ΔRij−1→∂bg∂ΔRij
∂ Δ R ‾ i j ∂ b ‾ g = ∑ k = i j − 1 ( − Δ R ‾ k + 1 j T J r k Δ t ) = ∑ k = i j − 2 ( − Δ R ‾ k + 1 j T J r k Δ t ) − Δ R ‾ j j T J r k Δ t = ∑ k = i j − 2 ( − ( Δ R ‾ k + 1 j − 1 Δ R ‾ j − 1 j ) T J r k Δ t ) − Δ R ‾ j j T J r k Δ t = − Δ R ‾ j − 1 j T ⋅ ∑ k = i j − 2 ( Δ R ‾ k + 1 j − 1 T J r k Δ t ) − Δ R ‾ j j T J r k Δ t = − Δ R ‾ j − 1 j T ⋅ ∂ Δ R ‾ i j − 1 ∂ b ‾ g − Δ R ‾ j j T ⏟ I J r k Δ t \begin{array}{l} \frac{\partial \Delta \overline{\mathbf{R}}_{i j}}{\partial \overline{\mathbf{b}}^{g}}=\sum_{k=i}^{j-1}\left(-\Delta \overline{\mathbf{R}}_{k+1 j}^{T} \mathbf{J}_{r}^{k} \Delta t\right) \\ =\sum_{k=i}^{j-2}\left(-\Delta \overline{\mathbf{R}}_{k+1 j}^{T} \mathbf{J}_{r}^{k} \Delta t\right) -\Delta \overline{\mathbf{R}}_{j j}^{T} \mathbf{J}_{r}^{k} \Delta t \\ =\sum_{k=i}^{j-2}\left(-\left(\Delta \overline{\mathbf{R}}_{k+1 j-1}\Delta \overline{\mathbf{R}}_{j-1 j} \right)^{T}\mathbf{J}_{r}^{k} \Delta t\right) -\Delta \overline{\mathbf{R}}_{j j}^{T} \mathbf{J}_{r}^{k} \Delta t \\ =-\Delta \overline{\mathbf{R}}_{ j-1 j}^{T}\cdot \sum_{k=i}^{j-2}\left(\Delta \overline{\mathbf{R}}_{k+1 j-1}^{T} \mathbf{J}_{r}^{k} \Delta t\right) -\Delta \overline{\mathbf{R}}_{j j}^{T} \mathbf{J}_{r}^{k} \Delta t \\ = -\Delta \overline{\mathbf{R}}_{ j-1 j}^{T}\cdot \frac{\partial \Delta \overline{\mathbf{R}}_{i j-1}}{\partial \overline{\mathbf{b}}^{g}} -\underbrace{\Delta \overline{\mathbf{R}}_{j j}^{T}}_{I} \mathbf{J}_{r}^{k} \Delta t \end{array} ∂bg∂ΔRij=∑k=ij−1(−ΔRk+1jTJrkΔt)=∑k=ij−2(−ΔRk+1jTJrkΔt)−ΔRjjTJrkΔt=∑k=ij−2(−(ΔRk+1j−1ΔRj−1j)TJrkΔt)−ΔRjjTJrkΔt=−ΔRj−1jT⋅∑k=ij−2(ΔRk+1j−1TJrkΔt)−ΔRjjTJrkΔt=−ΔRj−1jT⋅∂bg∂ΔRij−1−I ΔRjjTJrkΔt
JRg = dRi.deltaR.transpose() * JRg - dRi.rightJ * dt;
完整代码
void Preintegrated::IntegrateNewMeasurement(const Eigen::Vector3f &acceleration, const Eigen::Vector3f &angVel, const float &dt)
{
// 保存imu数据,利用中值积分的结果构造一个预积分类保存在mvMeasurements中
mvMeasurements.push_back(integrable(acceleration, angVel, dt));
// Position is updated firstly, as it depends on previously computed velocity and rotation.
// Velocity is updated secondly, as it depends on previously computed rotation.
// Rotation is the last to be updated.
// Matrices to compute covariance
// Step 1.构造协方差矩阵
// 噪声矩阵的传递矩阵,这部分用于计算i到j-1历史噪声或者协方差
Eigen::Matrix<float, 9, 9> A;
A.setIdentity();
// 噪声矩阵的传递矩阵,这部分用于计算j-1新的噪声或协方差,这两个矩阵里面的数都是当前时刻的,计算主要是为了下一时刻使用
Eigen::Matrix<float, 9, 6> B;
B.setZero();
// 考虑偏置后的加速度、角速度
Eigen::Vector3f acc, accW;
acc << acceleration(0) - b.bax, acceleration(1) - b.bay, acceleration(2) - b.baz;
accW << angVel(0) - b.bwx, angVel(1) - b.bwy, angVel(2) - b.bwz;
// 记录平均加速度和角速度
avgA = (dT * avgA + dR * acc * dt) / (dT + dt);
avgW = (dT * avgW + accW * dt) / (dT + dt);
// Update delta position dP and velocity dV (rely on no-updated delta rotation)
// 根据没有更新的dR来更新dP与dV eq.(38)
dP = dP + dV * dt + 0.5f * dR * acc * dt * dt;
dV = dV + dR * acc * dt;
// Compute velocity and position parts of matrices A and B (rely on non-updated delta rotation)
// 根据η_ij = A * η_i,j-1 + B_j-1 * η_j-1中的A矩阵和B矩阵对速度和位移进行更新
Eigen::Matrix<float, 3, 3> Wacc = Sophus::SO3f::hat(acc);
A.block<3, 3>(3, 0) = -dR * dt * Wacc;
A.block<3, 3>(6, 0) = -0.5f * dR * dt * dt * Wacc;
A.block<3, 3>(6, 3) = Eigen::DiagonalMatrix<float, 3>(dt, dt, dt);
B.block<3, 3>(3, 3) = dR * dt;
B.block<3, 3>(6, 3) = 0.5f * dR * dt * dt;
// Update position and velocity jacobians wrt bias correction
// 因为随着时间推移,不可能每次都重新计算雅克比矩阵,所以需要做J(k+1) = j(k) + (~)这类事,分解方式与AB矩阵相同
// 论文作者对forster论文公式的基础上做了变形,然后递归更新,参见 https://github.com/UZ-SLAMLab/ORB_SLAM3/issues/212
JPa = JPa + JVa * dt - 0.5f * dR * dt * dt;
JPg = JPg + JVg * dt - 0.5f * dR * dt * dt * Wacc * JRg;
JVa = JVa - dR * dt;
JVg = JVg - dR * dt * Wacc * JRg;
// Update delta rotation
// Step 2. 构造函数,会根据更新后的bias进行角度积分
IntegratedRotation dRi(angVel, b, dt);
// 强行归一化使其符合旋转矩阵的格式
dR = NormalizeRotation(dR * dRi.deltaR);
// Compute rotation parts of matrices A and B
// 补充AB矩阵
A.block<3, 3>(0, 0) = dRi.deltaR.transpose();
B.block<3, 3>(0, 0) = dRi.rightJ * dt;
// 小量delta初始为0,更新后通常也为0,故省略了小量的更新
// Update covariance
// Step 3.更新协方差,frost经典预积分论文的第63个公式,推导了噪声(ηa, ηg)对dR dV dP 的影响
C.block<9, 9>(0, 0) = A * C.block<9, 9>(0, 0) * A.transpose() + B * Nga * B.transpose(); // B矩阵为9*6矩阵 Nga 6*6对角矩阵,3个陀螺仪噪声的平方,3个加速度计噪声的平方
// 这一部分最开始是0矩阵,随着积分次数增加,每次都加上随机游走,偏置的信息矩阵
C.block<6, 6>(9, 9) += NgaWalk;
// Update rotation jacobian wrt bias correction
// 计算偏置的雅克比矩阵,r对bg的导数,∂ΔRij/∂bg = (ΔRjj-1) * ∂ΔRij-1/∂bg - Jr(j-1)*t
// 论文作者对forster论文公式的基础上做了变形,然后递归更新,参见 https://github.com/UZ-SLAMLab/ORB_SLAM3/issues/212
// ? 为什么先更新JPa、JPg、JVa、JVg最后更新JRg? 答:这里必须先更新dRi才能更新到这个值,但是为什么JPg和JVg依赖的上一个JRg值进行更新的?
JRg = dRi.deltaR.transpose() * JRg - dRi.rightJ * dt;
// Total integrated time
// 更新总时间
dT += dt;
}