用微分方程描述的连续时间滤波器举例

  在许多应用中，频率选择性滤波器是用线性常系数微分或差分方程描述的线性时不变系统来实现的。这有许多理由，例如很多具有滤波作用的物理系统都是由微分或差分方程表征的。这方面的一个很好的例子就是在后续将研究的汽车减震系统，在某种程度上这个系统的设计就是为了滤掉由道路表面不平坦引起的高频颠簸和起伏。利用由微分或差分方程描述的滤波器的第二个原因是，它们能很方便地用模拟硬件或数字硬件来实现。另外，由微分或差分方程描述的系统提供了一个极为广泛而灵活的设计空间，例如它可以得到一个很近似于理想的滤波器，或具有所要求的其他特性的滤波器。本讲将研究几个例子，用以说明如何利用微分和差分方程来实现连续时间和离散时间频率选择性滤波器。后续还会见到这类滤波器的其他一些例子，并且一定会对使此类滤波器如此有用的些性质得到更深入的理解。

简单 RC 低通滤波器

图1. 一阶RC滤波器

电路广泛用于实现连续时间滤波功能。其中最简单的一个例子就是示于图 1 的一阶 RC 电路，图中电压源$v_s(t)$是系统的输入。这个电路既能用来实现低通滤波，又能用来实现高通滤波，这取决于以什么作为输出信号。假定取电容器上的电压$v_c(t)$作为输出，这时输出电压和输入电压就由下列常系数微分方程所表示：

$$RC\frac{\mathrm{d}{v}_c(t)}{\mathrm{d}t}+v_c(t)=v_s(t)\text{\hspace{1em}(1)}$$

假定系统为最初松弛的，由上式描述的系统就是线性时不变的。为了确定频率响应$H(j\omega )$，根据定义，当输入电压$v_s(t)=e^{j\omega t}$时，输出电压一定是$v_c(t)=H(j\omega t)e^{j\omega t}$，将这些代入（1）式，可得
$$RC\frac{\mathrm{d}}{\mathrm{d}t}\left[H(j\omega ){\mathrm{e}}^{j\omega t}\right]+H(j\omega ){\mathrm{e}}^{j\omega t}={\mathrm{e}}^{j\omega t}$$
或者
$$RCj\omega H(j\omega ){\mathrm{e}}^{j\omega t}+H(j\omega ){\mathrm{e}}^{j\omega t}={\mathrm{e}}^{j\omega t}$$
由此可直接得出
$$H(j\omega ){\mathrm{e}}^{j\omega t}=\frac{1}{1+RCj\omega }{\mathrm{e}}^{j\omega t}$$
或
$$H(j\omega )=\frac{1}{1+RCj\omega }$$
幅频响应为
$$|H(j\omega )|=\frac{1}{\sqrt{1+(RC\omega {)}^2}}$$

相频响应为
$$\angle H(j\omega )=-\arctan (RC\omega )$$

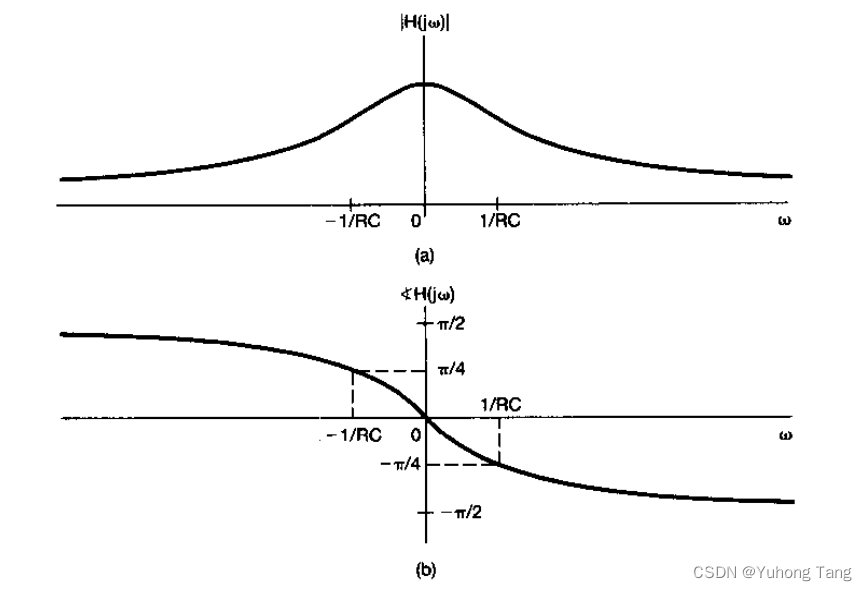
该例的频率响应$H(j\omega )$的模和相位如图 2 所示。应该注意到，在频率$\omega =0$附近，$|H(j\omega )|\approx 1$；而在较大的$\omega$值时（正值或负值），$|H(j\omega )|$显著较小，事实上就是随$|\omega |$增加而平缓地减小。因此，这一简单的 RC 滤波器，在以$v_c(t)$为输出的情况下就是一个非理想的低通滤波器。

图2. （a）和（b）分别是RC电路以电容电压作为输出的频率响应的模和相位图

简单 RC 高通滤波器

将 RC 电路的输出选为电阻两端的电压是另一种选择输出的方式。这时，关联输入和输出的微分方程是
$$RC\frac{\mathrm{d}{v}_r(t)}{\mathrm{d}t}+v_r(t)=RC\frac{\mathrm{d}{v}_s(t)}{\mathrm{d}t}$$

幅频响应为
$$|G(j\omega )|=\frac{1}{\sqrt{1+\frac{1}{(\omega RC{)}^2}}}$$

相频响应为
$$\angle G(j\omega )=-\arctan \left(\frac{1}{\omega RC}\right)$$

图 3所示为这个系统频率响应的模和相位。由图可见，该系统衰减掉较低的频率，而让较高的频率通过；也就是对于$|\omega |\gg 1/RC$的频率有最小的衰减。这就是说，该系统是一个非理想的高通滤波器。

图3. （a）和（b）分别是RC电路以电阻电压作为输出的频率响应的模和相位图

参考文献：
【1】Alan V Oppenheim, Alan S. Willsky. Signals and Systems, 2nd edition.