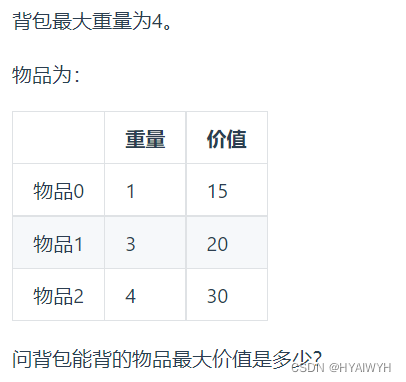
---

思路：

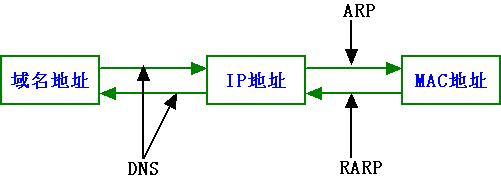
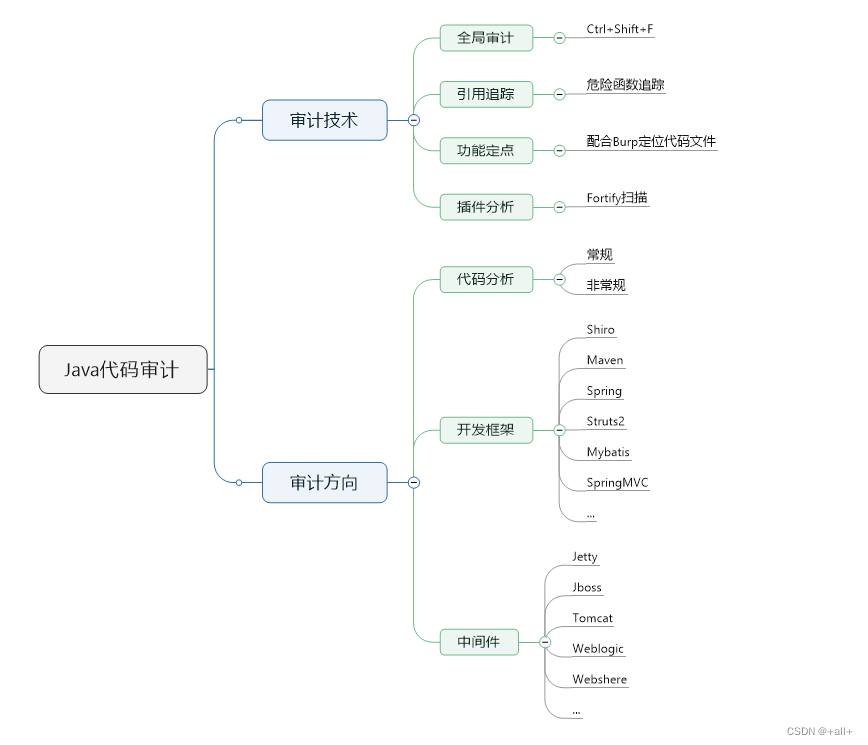
二维数组

动规五部曲

1、确定dp数组以及下标含义：二维数组dp[i][j]表示从下标为0-i的物品里任意取，放入容量为j的背包，价值总和最大为多少；
2、确定递推关系式：从两个方向推dp[i][j]，没放物品i以及放了物品i。没放物品i，由dp[i-1][j](当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同),放了物品i，由dp[i-1][j-weight[i]]+value[i]，也就模拟了物品i放入后得到的价值。因此递推关系式为：dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])。
3、初始化：背包容量为0时，一定为0；由递推关系可知i状态的价值由i-1状态推导而来，所以物品0的状态都需要初始化，即dp[0][j]。
4、确定遍历顺序：有两种遍历维度，物品与背包重量，先遍历物品更好理解。
5、举例推导dp数组。

void test() {
    vector<int> weight = { 1,3,4,1 };
    vector<int> value = { 15,20,40,25};
    int bagweight = 4;
    //初始化
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
    for (int i = weight[0]; i <= bagweight; i++) 
    {
        dp[0][i] = value[0];
    }
    //两个维度的遍历，先遍历物品，再遍历背包
    for (int i = 1; i < weight.size(); i++)
    {
        for (int j = 1; j <= bagweight; j++)
        {
            if (j < weight[i]) dp[i][j] = dp[i - 1][j];//物品i没放进来
            else  dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        }
    }
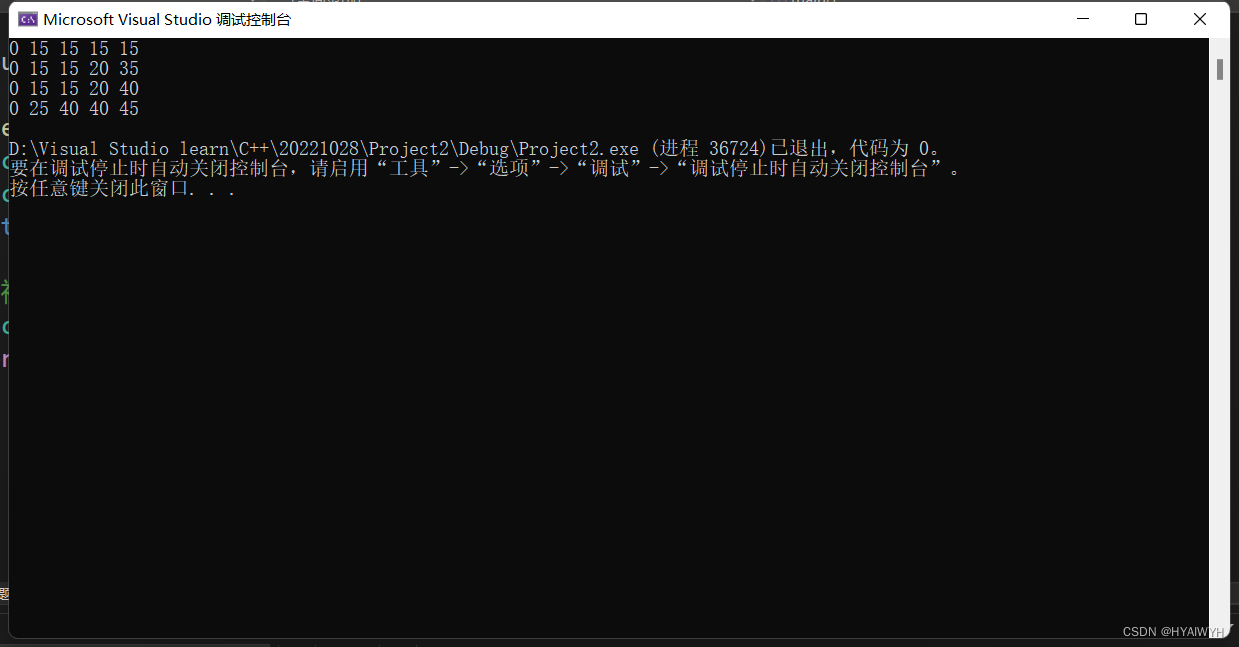
    cout << dp[weight.size() - 1][bagweight] << endl;
}
int main()
{
    test();
}

---

滚动数组

如果将dp[i-1]那层的数据都拷贝到dp[i]那一层，递推公式其实可以变为：dp[i][j]=max(dp[i][j],dp[i][j-weight[i]]+value[i])。
只用一个一维数组来实现，即滚动数组。能用滚动数组的条件是：上一层可以重复利用，直接拷贝到当前层。

动规五部曲
1、dp数组的意义：dp[j]表示容量为j的背包最大价值为dp[j]。
2、递推关系式：dp[j]可以通过dp[j-weight[i]]推导，dp[j]=max(dp[j],dp[j]-weight[i]+value[i])。
3、初始化：如果价值都大于0的话，刚开始的时候都初始化为0即可。
4、确定遍历顺序：先物品再背包，注意这里遍历背包的时候是从大到小。倒序的目的是为了保证物品i只被放入了一次，从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。 注意终止条件：for(int j = bagWeight; j >= weight[i]; j--)
5、举例推导dp数组。

void test01() {
    vector<int> weight = { 1,3,4,1 };
    vector<int> value = { 15,20,40,25 };
    int bagweight = 4;
    
    //初始化
    vector<int> dp(bagweight + 1, 0);
    for (int i = 0; i < weight.size(); i++)
    {
        for (int j = bagweight; j >= weight[i]; j--)//背包倒序
        {
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
        for_each(dp.begin(), dp.end(), [=](int x) {cout << x << " "; });
        cout << endl;
    }
    //cout << dp[bagweight] << endl;

}
int main()
{
    test01();
}

将每一次都打印出来，其实发现和二维数组是一样的，节省了空间复杂度。