题目描述：

chal_sage部分：

from Crypto.Util.number import *
from random import *
from secrets import flag


def gen_random(seed, P, Q, r_list, times):
    s = seed
    for i in range(times):
        s = int((s * P)[0])
        r = int((s * Q)[0])
        r_list.append(r)
    return r_list

def gen_seed():
    seed = getRandomNBitInteger(32)
    return seed

def getP_Q():
    Q = Curve.random_point()
    P = 114514*Q
    return P, Q

def enc(flag, rlist):
    seq = list(randint(0, 1) for _ in range(4))
    add = rlist[55]*(seq[0]*rlist[66] + seq[1]*rlist[77] + seq[2]*rlist[88] + seq[3]*rlist[99])
    xor = pow(rlist[114], rlist[514], rlist[233]*rlist[223])
    enc = (bytes_to_long(flag)^^xor)+add
    return enc

nums = 600

seed = gen_seed()

p = 58836547289031152641641668761108233140346455328711205590162376160181002854061
F = GF(p)
a = F(114)
b = F(514)
Curve = EllipticCurve(F, [a, b])
P, Q = getP_Q()
r_list = []
r_list = gen_random(seed, P, Q, r_list, nums)
ENCFLAG = enc(flag, r_list)
print(ENCFLAG)
print(P, Q)
print(r_list[0])

'''
4911741083112145038719536311222612998219730565328651097326896414315857050336523018712625917027324116103593300559128797807261543857571883314990480072241188
#####################################
#####################################
Oh no, P, Q and r_list[0] are accidentally lost, but John seems to know, you can ask him about these missing values ::>_<::
'''

homework部分：

from Crypto.Util.number import *
from params import N, E, D
from leak_data import P, Q, r_1
import re

def challenge():
    meum = '''option:
    1: get pubkey
    2: get sign
    3: verify
    4: exit'''
    print("Hi, I am John. If you help me with my homework, I'll give you the data that I know (￣o￣) . z Z")
    print(meum)
    sign = None

    while True:
        print('[+]input your option: ', end='')
        your_input = input()

        if your_input == '1':
            print(f'[+]N = {N}')
            print(f'[+]e = {E}')
            continue

        elif your_input == '2':
            sign = pow(bytes_to_long(MSG.encode()), D, N)
            print(f'[+]sign = {sign}')
            continue

        elif your_input == '3':
            if sign is None:
                print('[+]Please input option 2 to generate sign first.')
                continue
            msg_user = input("[+]Please input your message: ")
            n = int(input("[+]Please input n: "))
            e = int(input("[+]Please input e: "))
            if e <= 3:
                print('[+]e is invalid')
                break
            else:
                if re.match(r'I can not agree more!!!$', msg_user):
                    if pow(bytes_to_long(msg_user.encode()), e, n) == sign:
                        print("Goooooooood! You are my hero! I can give you the data that I know ╰(*°▽°*)╯")
                        print(f'Leak_data: \n P={P}\n Q={Q}\n first num in r_list={r_1}')
                        break
                    else:
                        print('[+]Error signature!')
                        break
                else:
                    print('[+]Error message!')
                    break

        elif your_input == '4':
            break

if __name__ == '__main__':
    MSG = 'This is an easy challenge'
    challenge()

题目分析：

import gmpy2
from Crypto.Util.number import *
N =   7399403457188876147280737704413998161465702407270784053949887695340528233758555062010898995255039810187699911928866167640259018538192441232641067730711771
E = 65537
sign = 1320070156891033288626051716868212806309097835600533098946778415708131349531482538706467629025443890643255446066240480813053241479563851572261696377893792
MSG = 'This is an easy challenge'
msg_user = 'I can not agree more!!!'

# pow(MSG,D,N) = pow(msg_user,e,n) = sign,要求e,n

# 题目中限制条件e > 3，那我就令e = 4或5喽，或者构造光滑数

pow(MSG,D,N) = pow(msg,e,n) = sign,求e,n

题目中限制条件e > 3，那我直接令e = 4或5咯，或者构造光滑数

法一（构造光滑数）：

from Crypto.Util.number import *

def gen_primes(nbit, imbalance):
    """
    :param nbit: 最终光滑数比特数
    :param imbalance: 最小单位比特数
    :return: 比特数
    """
    p = int(2)
    FACTORS = [p]
    while p.bit_length() < nbit - 2 * imbalance:
        factor = getPrime(imbalance)
        FACTORS.append(factor)
        p *= factor
    rbit = (nbit - p.bit_length()) // 2

    while True:
        r, s = [getPrime(rbit) for _ in '01']
        _p = p * r * s
        if _p.bit_length() < nbit: rbit += 1
        if _p.bit_length() > nbit: rbit -= 1
        if isPrime(_p + 1):
            FACTORS.extend((r, s))
            p = _p + 1
            break

    FACTORS.sort()
    return (p, FACTORS)

MSG = 'This is an easy challenge'
msg = 'I can not agree more!!!'
sign = 1320070156891033288626051716868212806309097835600533098946778415708131349531482538706467629025443890643255446066240480813053241479563851572261696377893792

M = bytes_to_long(MSG.encode())
m = bytes_to_long(msg.encode())

n, n_fac = gen_primes(512, 20)
# n = 4042948769941627341019324611789396195045815639020219860408774627904312552947443280269093998428541432391837271401229040233775660233089444891431013462995967

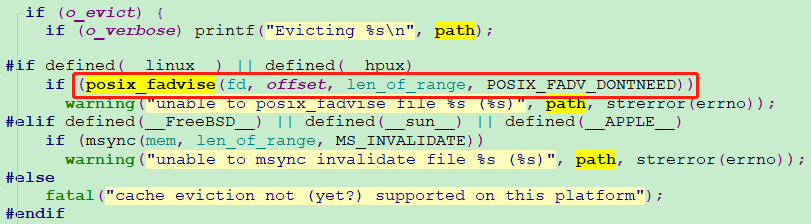
离散对数sage求解（模数小 / 阶光滑）

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IfNXFlc6-1687436645430)(C:\Users\Emma\AppData\Roaming\Typora\typora-user-images\image-20230621233649390.png)]$

# h = g^x mod p
# c1 = m^e mod n1
p = n
g = m
h = sign
x = discrete_log(Mod(h,p),Mod(g,p))
print(pow(m,x,p)==sign)
print('n =', p)
print('e =', x)

也可以直接：

n = 4042948769941627341019324611789396195045815639020219860408774627904312552947443280269093998428541432391837271401229040233775660233089444891431013462995967
G = Zmod(n)
m1 = G(m)
c1 = G(sign)
print(ZZ(discrete_log(c1,m1)))

这部分好像好像好像啊！discrete_log：

a=2275123956203765363233765961297507379124236980967603145079239177208264523438555378298177602517599708533004805369986246098127863480798528206818576888655427591685534478161571717613561380234338516607855593046949
fac = [2, 136327, 169937, 313351, 321427, 323377,356887, 413783, 519733,792413, 860077, 906289, 976501]
G=Zmod(N)
m1=G(m)
c1=G(a)
oo=[]
for i in fac:
    h=(N-1)//i
    dlp1=discrete_log(c1**h,m1**h)
    oo.append(int(dlp1))
sk=crt(oo,fac)
mod = prod(fac)
for i in range(100):
    print(long_to_bytes(int(sk + i * mod)))
    
# 或：    
m = 1391372358062724416224243990838035874507346098208831800403257
a=2275123956203765363233765961297507379124236980967603145079239177208264523438555378298177602517599708533004805369986246098127863480798528206818576888655427591685534478161571717613561380234338516607855593046949
G=Zmod(N) 
m1=G(m) 
c1=G(a) 
print(long_to_bytes(ZZ(discrete_log(c1,m1))))
# Neepu{Nsmoothnumber}

方法二：

MSG = 'This is an easy challenge'
msg = 'I can not agree more!!!'
sign = 1320070156891033288626051716868212806309097835600533098946778415708131349531482538706467629025443890643255446066240480813053241479563851572261696377893792
e = 4
n = bytes_to_long(msg.encode())**e - sign 
print('e = ',e)
print('n = ',n)

接下来求后面部分：

s1 = int((s0 * P)[0])
r1 = int((s1 * Q)[0])
P  = 114514 * Q 

s1 = (seed * P).x，
r1 = (s1 * Q).x = rlist[0]
s2 = (s1 * P).x 
===> s2 = (s1 * 114514 * Q).x
        = (114514 * s1 * Q).x 
        = (114514*Curve.lift_x(r0))[0] 
        
(PS:Curve.lift_x() 方法会在给定的 x 坐标上搜索相应的 y 值，以获得椭圆曲线上的曲线点。
结果返回的是一个曲线点对象，包含了曲线上的 x 和 y 坐标)

# sage
from Crypto.Util.number import * 
nums = 600
 
p = 58836547289031152641641668761108233140346455328711205590162376160181002854061
F = GF(p)
a = F(114)
b = F(514)
E = EllipticCurve(F,[a, b])

P=E(24181776889473219401017476947331354458592459788552219617833554538756564211844, 33783050059316681746742286692492975385672807657476634456871855157562656976035)
Q=E(16104852983623236554878602983757606922134442855643833150623643268638509292839, 3562830444362909774600777083869972812060967068803593091854731534842281574275)
r0 = 50920555924101118476219158701093345090627150442059647242030060086626996278598
rlist = [r0]
for _ in range(600):
    s = (E.lift_x(rlist[-1]) * 114514)[0]
    rlist.append((int(s) * Q)[0])
    
r_list = [r0]
for i in range(515):
    R0 = E.lift_x(r_list[-1])
    s1 = ZZ((114514 * R0)[0])
    r1 = ZZ((s1*Q)[0])
    r_list.append(r1)
    
rlist = [int(i) for i in rlist] # 不可少
'''
没加这行rlist中数据类型<class 'sage.rings.integer.Integer'>
加了这行rlist中数据类型<class 'int'>
在Sage中，Integer是一个类，而int是Python的内置数据类型。与Java类似，在使用Sage中的Integer时，需要通过调用其方法或属性将其转换为Python的int类型才能进行数值计算或比较等操作。虽然Sage中的Integer与Python的int都可以表示整数，但它们的底层实现略有不同
'''

for i in range(2 ^ 4):
    seq = [(i >> 3) & 1, (i >> 2) & 1, (i >> 1) & 1, i & 1]
    add = rlist[55]*(seq[0]*rlist[66] + seq[1]*rlist[77] + seq[2]*rlist[88] + seq[3]*rlist[99])
    xor = pow(rlist[114], rlist[514], rlist[233]*rlist[223])
    flag = long_to_bytes(int((enc - add) ^^ xor))
    if b'SCTF' in flag:
        print(flag)
# b'SCTF{Th1s_i5_my_happy_s0ng_I_like_to_5ing_it_@ll_day_1ong}'