机器学习 | 实验五：LDA

news2024/9/21 0:25:46

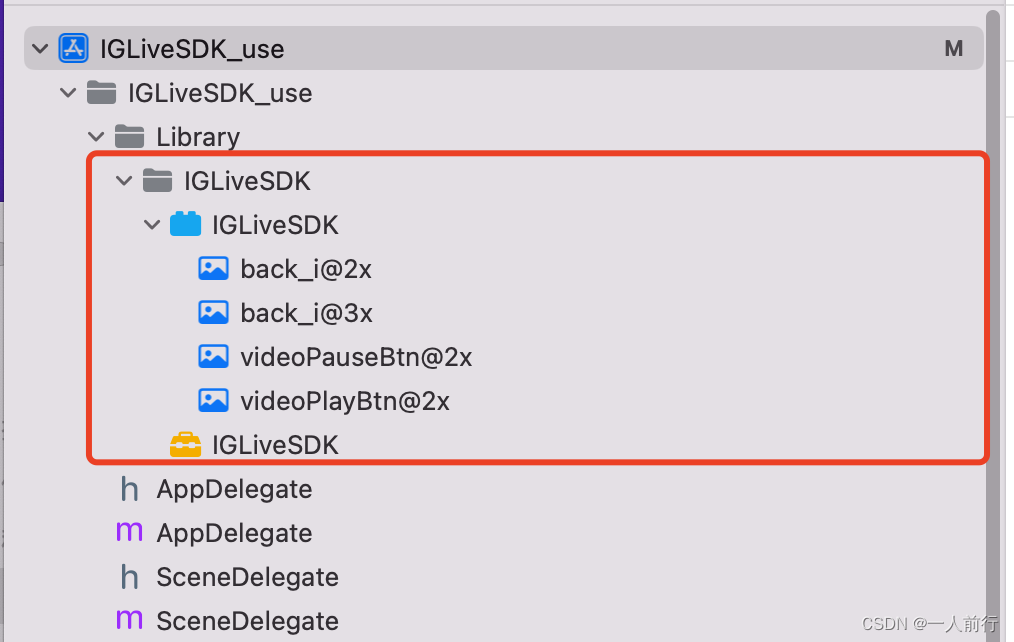
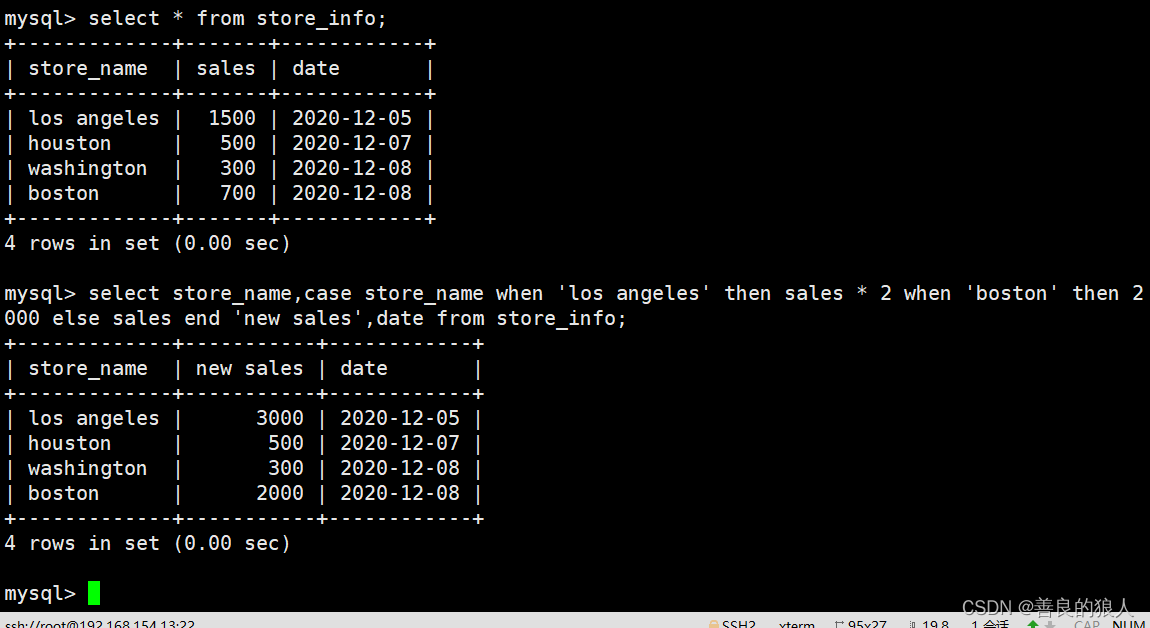
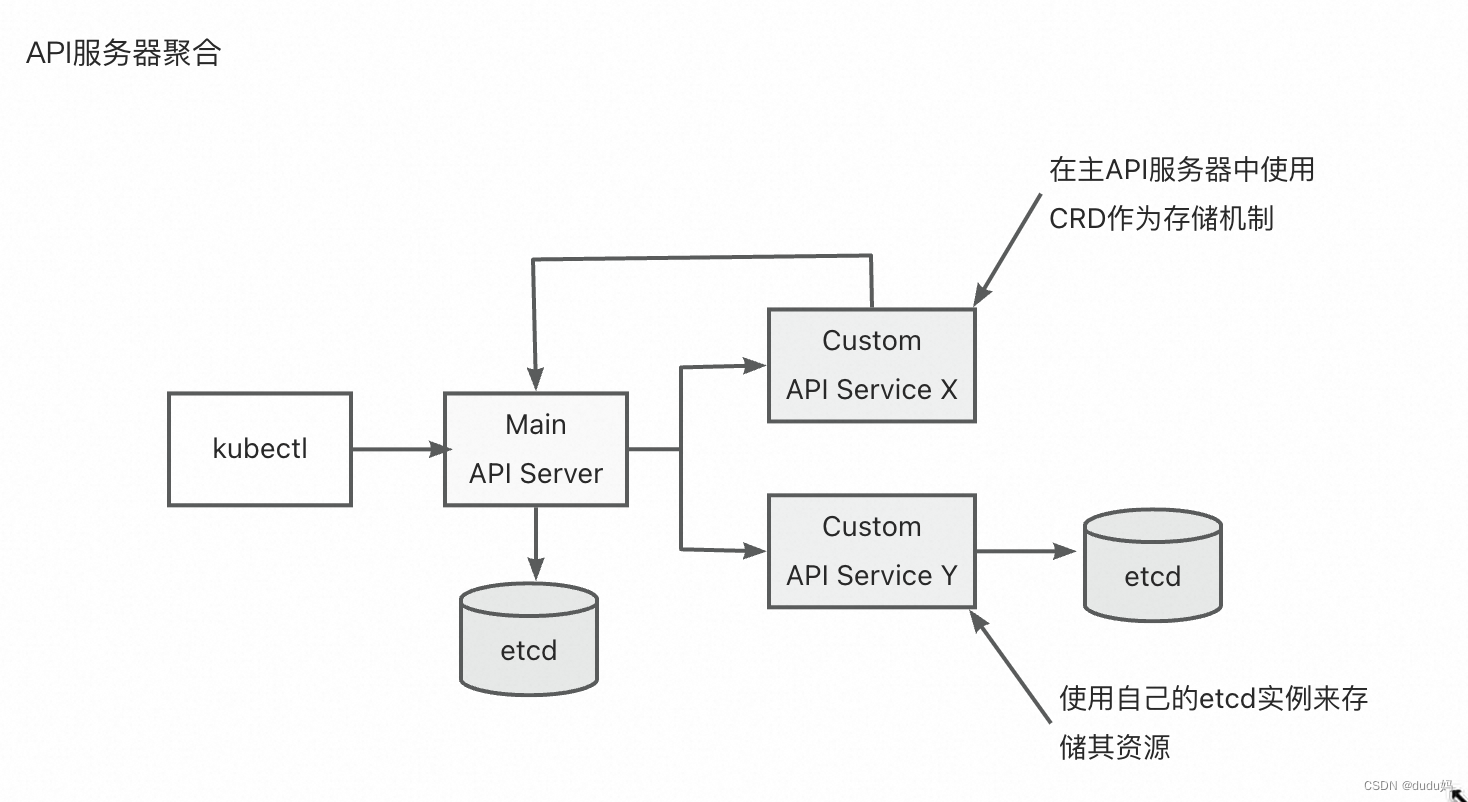
LDA的思想：“投影后类内方差最小，类间方差最大”。即数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。

假设我们有两类数据分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

在这里插入图片描述

LDA将带有标签的数据降维，投影到低维空间同时满足三个条件：

  • 尽可能多的保留数据样本的信息（即选择最大的特征是对应的特征向量所代表的方向）。
  • 寻找最佳投影方向以更好区分不同类样本。
  • 投影后使得同类样本尽可能近，不同类样本尽可能远。

📚描述

在本练习中，您需要实现线性判别分析（LDA）。

📚数据

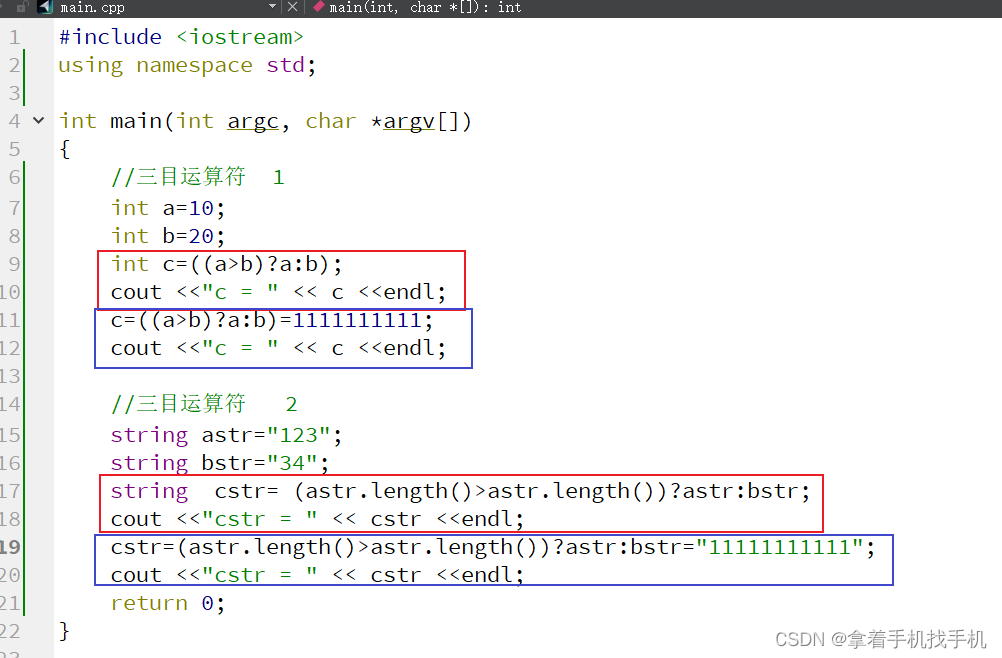
在这个练习中，在ex3red.dat中有14行（x，y）红点，在ex3blue.dat和ex3green.dat中分别有14行蓝点和绿点。您应该使用它们来实现LDA。

📚LDA

🐇二维LDA

在本节中，需要实现2个类的LDA。这里我们选择对这两个类使用红点和蓝点。您应该将数据加载到矩阵中，并绘制它们：

x1=load('ex3red.dat');
x2=load('ex3blue.dat');
x3=load('ex3green.dat');
figure 
hold on
plot(x1(:,1),x1(:,2),'ro','markerfacecolor','r');
plot(x2(:,1),x2(:,2),'b*','markerfacecolor','b');
xlabel('x');
ylabel('y');
xlim([0.00 10.00])
ylim([0.00 10.00])

在这里插入图片描述

m1=mean(x1);
m2=mean(x2);
Sb=(m1-m2)'*(m1-m2);
Sw=(x1-m1)'*(x1-m1)+(x2-m2)'*(x2-m2);
[V,L]=eig(inv(Sw)*Sb);
[a,b]=max(max(L));
theta = Sw\(m1-m2)';
disp(theta)
figure
hold on
plot(x1(:,1),x1(:,2),'ro','markerfacecolor','r');
plot(x2(:,1),x2(:,2),'b*','markerfacecolor','b');
x=linspace(0,10,100);
y=(theta(2)/theta(1))*x;
plot(x,y,'black')
title('LDA for two-classes')
xlabel('x')
ylabel('y')

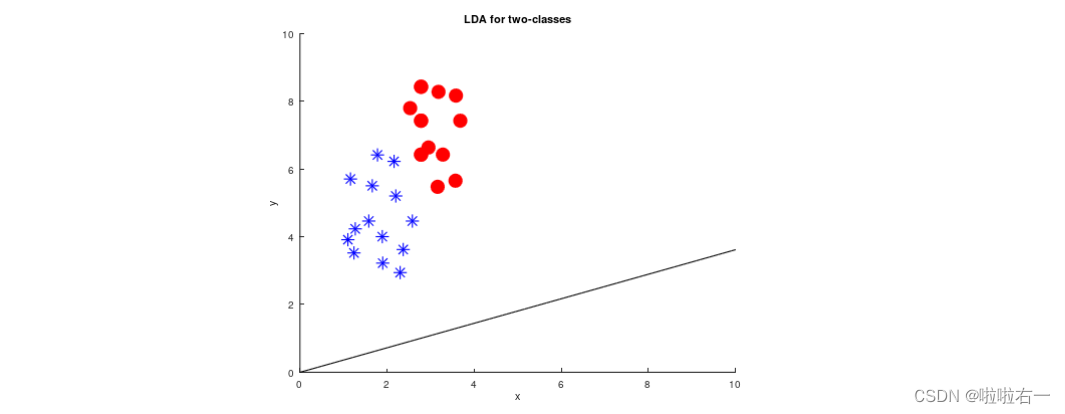
一旦您成功地完成了您的代码，LDA的结果应该如下所示：

k=theta(2)/theta(1);
s1=size(x1,1);
s2=size(x2,1);
x1_tag=[];
x2_tag=[];
for i=1:s1
    y0=x1(i,2);
    x0=x1(i,1);
    xn=(k*(y0-b)+x0)/(k^2+1);
    x1_tag=[x1_tag;xn];
end
y1_tag=k*x1_tag + b;
x1_final=[x1_tag y1_tag];
for i=1:s2
    y0=x2(i,2);
    x0=x2(i,1);
    xn=(k*(y0-b)+x0)/(k^2+1);
    x2_tag=[x2_tag;xn];
end
y2_tag=k*x2_tag + b;
x2_final=[x2_tag y2_tag];
figure
hold on
plot(x1(:,1),x1(:,2),'ro','markerfacecolor','r');
plot(x2(:,1),x2(:,2),'b*','markerfacecolor','b');
x=linspace(0,10,100);
y=(theta(2)/theta(1))*x + b;
plot(x,y,'black')
title('LDA for two-classes')
xlabel('x')
ylabel('y')
plot(x1_final(:,1),x1_final(:,2),'ro','markerfacecolor','r');
plot(x2_final(:,1),x2_final(:,2),'bo','markerfacecolor','b');

同时，可以将红点和蓝点投影到直线上，看到投影点如下：

在这里插入图片描述

🐇N维LDA

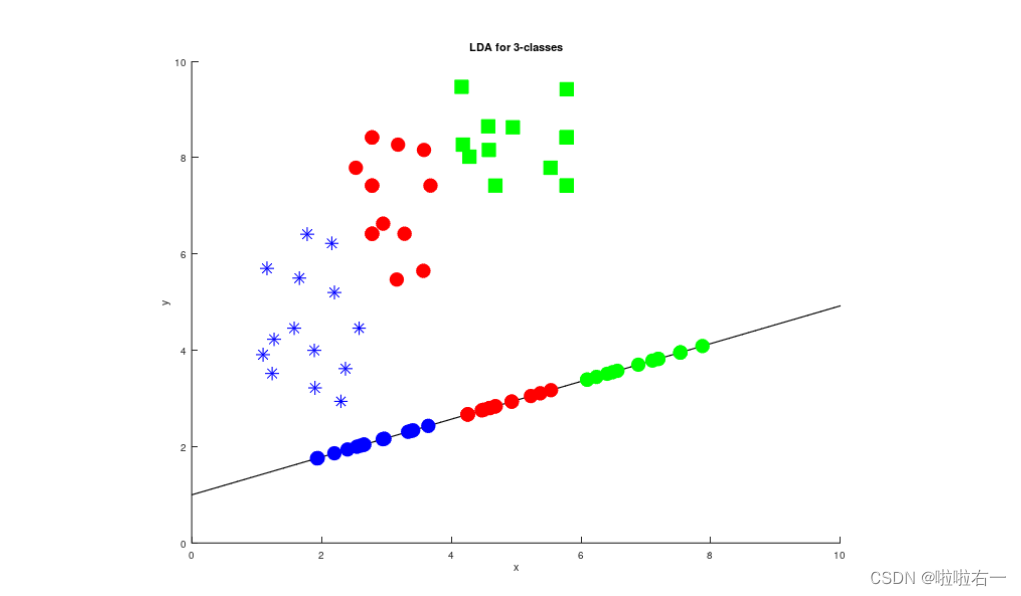
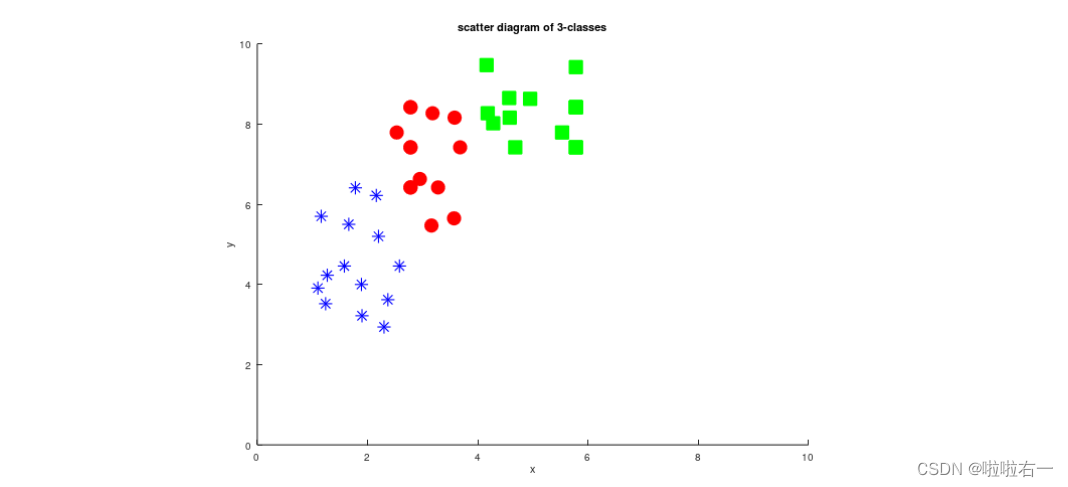
LDA可以为N个类实现。在本节中，您应该实现N个类的LDA，其中N为3。将所有的红、蓝、绿点加载到矩阵中，并绘制出它们。

x1=load('ex3red.dat');
x2=load('ex3blue.dat');
x3=load('ex3green.dat');
figure
hold on
plot(x1(:,1),x1(:,2),'ro','markerfacecolor','r');
plot(x2(:,1),x2(:,2),'b*','markerfacecolor','b');
plot(x3(:,1),x3(:,2),'gs','markerfacecolor','g');
xlabel('x');
ylabel('y');
title('scatter diagram of 3-classes');
xlim([0.00 10.00]);
ylim([0.00 10.00]);

在这里插入图片描述

计算类内散度矩阵和类间散度矩阵。绘制直线。

hold off
m1=mean(x1);%compute mean value
m2=mean(x2);
m3=mean(x3);
m=mean([x1;x2;x3]);
%LDA for 3-class
Sb=((m1-m)'*(m1-m)+(m2-m)'*(m2-m)+(m3-m)'*(m3-m))/3;%compute Between-class scatter
Sw=((x1-m1)'*(x1-m1)+(x2-m2)'*(x2-m2)+(x3-m3)'*(x3-m3))/3;%compute Within-class scatter
%LDA for N class where N=3
[V,L]=eig(inv(Sw)*Sb);
[a,b]=max(max(L));% The eigenvector corresponds to the largest eigenvalue.
theta = V(:,b);
k=theta(2)/theta(1);%calculate the slope
figure%figure 2
hold on
plot(x1(:,1),x1(:,2),'ro','markerfacecolor','r');
plot(x2(:,1),x2(:,2),'b*','markerfacecolor','b');
plot(x3(:,1),x3(:,2),'gs','markerfacecolor','g');
xlim([0.00 10.00]);
ylim([0.00 10.00]);
xlabel('x');
ylabel('y');
x=linspace(0,10,100);
y=k*x+b;
plot(x,y,'black')
title('LDA for 3-classes')
xlabel('x')
ylabel('y')

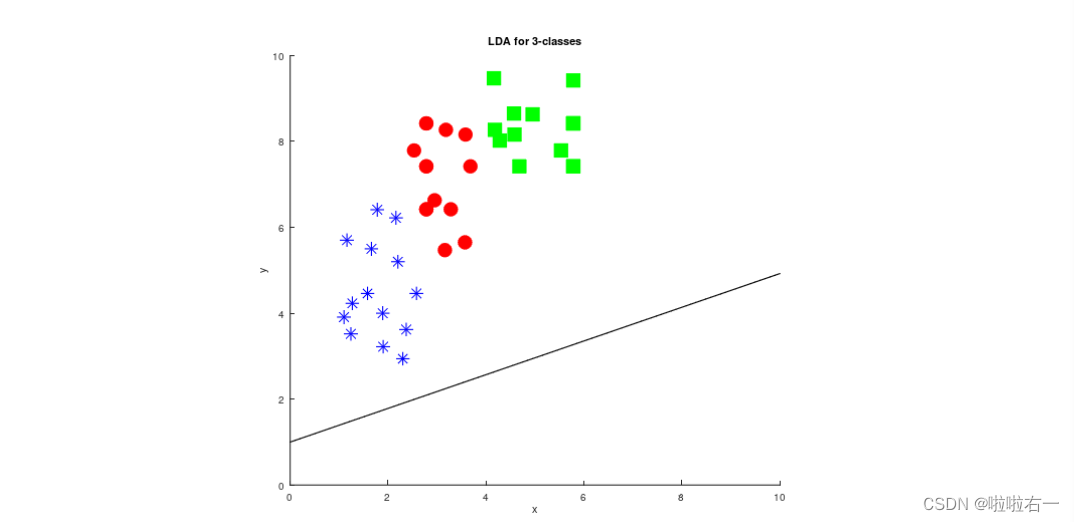
在这里插入图片描述

投影

hold off
s1=size(x1,1);
s2=size(x2,1);
s3=size(x3,1);
x1_tag=[];
x2_tag=[];
x3_tag=[];
for i=1:s1
    y0=x1(i,2);
    x0=x1(i,1);
    xn=(k*(y0-b)+x0)/(k^2+1);
    x1_tag=[x1_tag;xn];
end
y1_tag=k*x1_tag + b;
x1_final=[x1_tag y1_tag];
for i=1:s2
    y0=x2(i,2);
    x0=x2(i,1);
    xn=(k*(y0-b)+x0)/(k^2+1);
    x2_tag=[x2_tag;xn];
end
y2_tag=k*x2_tag + b;
x2_final=[x2_tag y2_tag];
for i=1:s3
    y0=x3(i,2);
    x0=x3(i,1);
    xn=(k*(y0-b)+x0)/(k^2+1);
    x3_tag=[x3_tag;xn];
end
y3_tag=k*x3_tag+b;
x3_final=[x3_tag y3_tag];
figure%third
hold on
plot(x1(:,1),x1(:,2),'ro','markerfacecolor','r');
plot(x2(:,1),x2(:,2),'b*','markerfacecolor','b');
plot(x3(:,1),x3(:,2),'gs','markerfacecolor','g');
xlim([0.00 10.00]);
ylim([0.00 10.00]);
x=linspace(0,10,100);
y=k*x+b;
plot(x,y,'black')
title('LDA for 3-classes')
xlabel('x')
ylabel('y')
plot(x1_final(:,1),x1_final(:,2),'ro','markerfacecolor','r');
plot(x2_final(:,1),x2_final(:,2),'bo','markerfacecolor','b');
plot(x3_final(:,1),x3_final(:,2),'go','markerfacecolor','g');

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/674314.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

关于socket编程中FD_XXX以及select函数的理解

关于socket编程中FD_XXX以及select函数的理解

文章目录 01 | 宏接口定义02 | 使用方法03 | 服务端代码示例 学习socket编程的时候看到很多FD开头的宏定义和函数，这里记录一下这些宏定义和函数的含义及处理流程 01 | 宏接口定义 fd_set fd_set 是一种表示文件描述符的集合类型，在socket编程中&#xf…
阅读更多...
计算机网络——自顶向下方法（第三章学习记录）

计算机网络——自顶向下方法（第三章学习记录）

本章学习运输层 运输层位于应用层和网络层之间，是分层的网络体系的重要部分，该层为运行在不同主机上的应用进程提供直接的通信服务起着至关重要的作用。 运输层协议为运行在不同主机上的应用进程之间提供了逻辑通信(logic communication)功能。从应用程…
阅读更多...
CSS3-补充-伪元素

CSS3-补充-伪元素

伪元素 作用：在网页中创建非主体内容，开发中常用CSS创建标签，比如装饰性的不重要的小图 区别： 1 元素：HTML 设置的标签 2 伪元素：由 CSS 模拟出的标签效果 …
阅读更多...
EMC学习笔记（七）阻抗控制（一）

EMC学习笔记（七）阻抗控制（一）

阻抗控制（一） 1.特征阻抗的物理意义1.1 输入阻抗1.2 特征阻抗1.3 偶模阻抗、奇模阻抗、差分阻抗 2.生产工艺对阻抗控制的影响 1.特征阻抗的物理意义 1.1 输入阻抗 在集总电路中，输入阻抗是经常使用的一个术语 ，它的物理意义是: …
阅读更多...
FreeRTOS实时操作系统（六）列表与列表项

FreeRTOS实时操作系统（六）列表与列表项

系列文章目录 文章目录 系列文章目录简要概念列表列表项迷你列表项 相关API函数初始化列表列表项初始化列表项插入（升序）末尾列表项插入列表项删除 实战实验 简要概念 列表是 FreeRTOS 中的一个数据结构，概念上和链表有点类似，列…
阅读更多...
ubuntu环境下测试硬盘读写速度

ubuntu环境下测试硬盘读写速度

在Ubuntu下，可以使用hdparm、dd和fio等工具来测试硬盘的读写速度。 开始之前，先使用sudo fdisk -l命令来列出系统中所有的硬盘和分区： 1.使用hdparm测试硬盘读取速度： 安装hdparm： sudo apt-get install hdparm 通…
阅读更多...
C++17中utf-8 character literal的使用

C++17中utf-8 character literal的使用

一个形如42的值被称作字面值常量(literal),这样的值一望而知。每个字面值常量都对应一种数据类型，字面值常量的形式和值决定了它的数据类型。 由单引号括起来的一个字符称为char型字面值，双引号括起来的零个或多个字符则构成字符串型字面值。 字符串字面…
阅读更多...
9.QT 三目运算符

9.QT 三目运算符

上面引出两个新的概念： 左值：能被赋值的就是左值。 右值：不能被赋值的就是右值。
阅读更多...
基於ranger，kerberos，hadoop ha 配置hvie多用戶

基於ranger，kerberos，hadoop ha 配置hvie多用戶

基於ranger，kerberos，hadoop ha 配置hvie多用戶 hive多用戶權限管理一、hive的管理員用戶二、hive配置普通用戶1.添加用戶2.配置kerberos2.1 创建主体2.2 生成keytab文件2.3 修改keytab文件所有者(可做可不做) 3. 配置windows hive多用戶權限管理 一、h…
阅读更多...
English Learning - L3 综合练习 8 TED-Living Beyond the Limits 2023.06.21 周三

English Learning - L3 综合练习 8 TED-Living Beyond the Limits 2023.06.21 周三

English Learning - L3 综合练习 8 TED-Living Beyond the Limits 2023.06.21 周三 句 1句 2扩展 句 3句 4句 5句 6句 7扩展 random 句 8扩展 句 9句 10句 11句 12句 13句 14句 15句 16句 17句 18句 19句 20句 21句 22句 23 句 1 Four months later I was back up on a snowbo…
阅读更多...
SVN使用步骤

SVN使用步骤

1.基本操作 2.提交之间看一下变更内容 3.显示日志 是查看所有提交的记录4.撤销和恢复操作 撤销本地修改 或者点击提交的时候 还原 把修改的撤销掉 第二种情况,内容已经提交上去了点击提交日志 进行操作 只是撤销了本地 接着还需要继续提交到服务端 第三种情况 我们需要恢…
阅读更多...
Linux系统之安装showdoc文档工具

Linux系统之安装showdoc文档工具

Linux系统之部署showdoc文档工具 一、showdoc介绍1.1 showdoc简介1.2 showdoc功能 二、本地环境介绍2.1 本地环境规划2.2 本次实践介绍 三、检查本地环境3.1 检查本地操作系统版本3.2 检查系统内核版本3.3 检查本地yum仓库状态 四、安装httpd服务4.1 安装httpd4.2 启动httpd服务…
阅读更多...
用Visual C++写出你第一个Windows程序

用Visual C++写出你第一个Windows程序

我是荔园微风，作为一名在IT界整整25年的老兵，今天来看看如何用Visual C写出你第一个Windows程序。 与其看很多Windows的书，不如先自己动手写一个Windows程序。由于Windows程序的特有机制，不建议去写那种简单的HELLO WORLD&#x…
阅读更多...
iOS 制作私有库framework + 图片资源的使用

iOS 制作私有库framework + 图片资源的使用

1. 库的分类 开源库：公开源代码，能看到具体实现** 闭源库**：不公开源代码，是经过编译后的二进制文件，看不到具体实现；其中包括：静态库和动态库 2. 开源库的制作 我了解的开源库的制作&#xff0…
阅读更多...
Python基础篇(一)：如何使用PyCharm创建第一个Python项目(包含tools)

Python基础篇(一)：如何使用PyCharm创建第一个Python项目(包含tools)

如何使用PyCharm创建第一个Python项目 前言1.创建Python项目2. 创建第一个python文件3. 编写运行第一个python程序4. 关于此工具的相关使用 前言 环境版本Python3.11.4PyCharm2023.1.2OSwindows10 PyCharm是一款由JetBrains开发的强大的Python集成开发环境（IDE&am…
阅读更多...
单个springboot整合rabbitmq

单个springboot整合rabbitmq

一、rabbitmq的搭建 centos7搭建rabbitmq:centos7安装rabbitmq_java-zh的博客-CSDN博客 二、在什么情况下选择rabbitMQ 常见的四种MQ比较 特 性ActiveMQRabbitMQRocketMQKafka语言JavaErlangJavaScala单机吞吐万万十万十万时效性msusmsms(以内)可用性高（主从架构…
阅读更多...
模拟电路系列分享-复杂阻容电路的频响

模拟电路系列分享-复杂阻容电路的频响

目录 概要 整体架构流程 技术名词解释 技术细节 1.基本变形 2.单元串联的粗略计算 3.推广结论 小结 概要 在基本单元电路的基础上，熟悉一些常见的变形电路，学会判断是高通还是低通，快速计算出截止频率是多少，对求解复杂电路的频率…
阅读更多...
TypeScript ~ 掌握基本类型 ①

TypeScript ~ 掌握基本类型 ①

作者 : SYFStrive 博客首页 : HomePage 📜： TypeScript ~ TS 📌：个人社区（欢迎大佬们加入） 👉：社区链接🔗 📌：觉得文章不错可以点点关注 &…
阅读更多...
MySQL高级sql语句操作二

MySQL高级sql语句操作二

MySQL高级sql语句操作二 一、EXISTS二、连接查询三、自我连接（算排名）四、CREATE VIEW（视图）五、UNION（联集）六、交集值七、无交集值八、CASE九、空值(NULL) 和 无值() 的区别十、正则表达式 一、EXISTS 用…
阅读更多...
Kubernetes学习笔记-kubernetes应用扩展-自定义API对象（1）20230622

Kubernetes学习笔记-kubernetes应用扩展-自定义API对象（1）20230622

1、CustomResourceDefinitions介绍 开发者只需要只需向kubernetes api服务器提交CRD对象，即可定义新的资源类型。成功提交CRD之后，就能通过API服务器提交JSON清单或者YAML清单的方式创建自定义资源，以及其他kubernetes资源实例 创建一个CRD…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023