目录
概要
整体架构流程
技术名词解释
技术细节
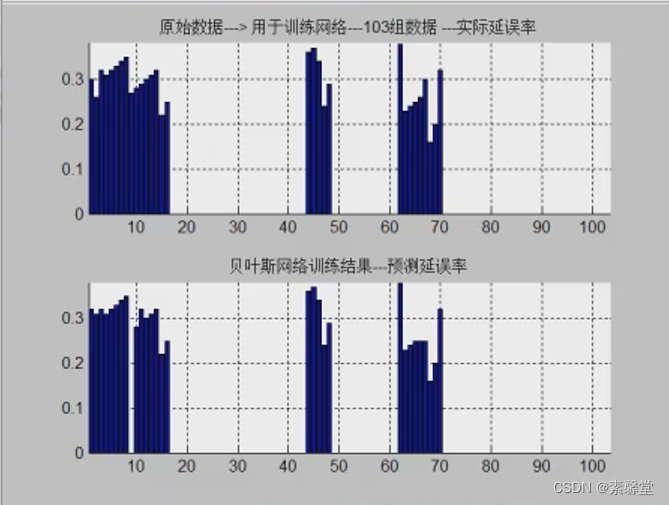
1.基本变形
2.单元串联的粗略计算
3.推广结论
小结
概要
在基本单元电路的基础上,熟悉一些常见的变形电路,学会判断是高通还是低通,快速计算出截止频率是多少,对求解复杂电路的频率响应非常有用。
整体架构流程

根据基本的低通和高通电路做的变换。

技术名词解释
高通:高通滤波器,又称低截止滤波器、低阻滤波器,允许高于某一截频的频率通过,而大大衰减较低频率的一种滤波器 。它去掉了信号中不必要的低频成分或者说去掉了低频干扰。
低通:低通滤波器是容许低于截止频率的信号通过, 但高于截止频率的信号不能通过的电子滤波装置。
相位:相位(phase)是对于一个波,特定的时刻在它循环中的位置:一种它是否在波峰、波谷或它们之间的某点的标度 [1] 。相位描述信号波形变化的度量,通常以度 (角度)作为单位,也称作相角。 当信号波形以周期的方式变化,波形循环一周即为360
滤波器:滤波器是由电容、电感和电阻组成的滤波电路。滤波器可以对电源线中特定频率的频点或该频点以外的频率进行有效滤除,得到一个特定频率的电源信号,或消除一个特定频率后的电源信号。滤波器是一种选频装置,可以使信号中特定的频率成分通过,而极大地衰减其他频率成分。利用滤波器的这种选频作用,可以滤除干扰噪声或进行频谱分析。换句话说,凡是可以使信号中特定的频率成分通过,而极大地衰减或抑制其他频率成分的装置或系统都称之为滤波器。滤波器,是对波进行过滤的器件。“波”是一个非常广泛的物理概念,在电子技术领域,“波”被狭义地局限于特指描述各种物理量的取值随时间起伏变化的过程。该过程通过各类传感器的作用,被转换为电压或电流的时间函数,称之为各种物理量的时间波形,或者称之为信号。因为自变量时间是连续取值的,所以称之为连续时间信号,又习惯地称之为模拟信号(Analog Signal)。滤波是信号处理中的一个重要概念,在直流稳压电源中滤波电路的作用是尽可能减小脉动的直流电压中的交流成分,保留其直流成分,使输出电压纹波系数降低,波形变得比较平滑。
技术细节
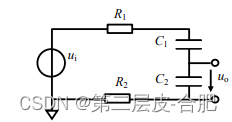
1.基本变形

推广结论为︰在一个电压源阻容串联回路中,如果从以任何一个电容两端电压为输出,那么它一定是一个低通电路,其上限截止频率为1/2nRC,其中R为回路中所有电阻之和,C为回路中所有电容的串联值(类似于电阻并联计算)。
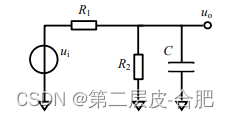
以上是一个戴维宁电路等效电路:
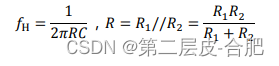

最后可以得出

对一个无源器件组成的电阻、电容(电感)网络,其输入可能是电压、电流,输出也可能是电压或者电流,而且阻容结构变化多端,一眼看出它是高通还是低通,或者什么都不是,似乎是个困难的任务。
两极判断法,可以较为轻松的实现上述判断,方法是︰
第一个极,是0Hz。此时电容容抗无穷大,在图中可以将其断开,此时求解电路增益,
称为A;
第二个极,是频率无穷大,电容容抗为0,在图中可以将其短路,求解此时的增益,称为Ao,然后按照下述规则判断︰
1如果A0为有限值,A无穷为0,则一定是低通。
2如果A无穷为有限值,A0为0,则一定是高通。
3除此之外,什么都不是∶既不是高通,也不是低通。
2.单元串联的粗略计算
将多个低通模块串联,最终仍是低通效果。将多个高通模块串联,最终仍是高通效果。其中,中频段增益Amo= Am*Amz*Am2。这很好理解。
串联后的截止频率稍复杂一些,但基本结论是∶对于高通串联,串联后的下限截止频率一定大于等于各个模块下限截止频率的最大值。对于低通串联,串联后的上限截止频率一定小于等于各个模块上限截止频率的最小值。多数情况下,可以简化处理。
在低通串联中,如果它们的上限截止频率中,最小上限截止频率与其它的存在较大差异时,最终上限截止频率就是那个最小的。这一点也好理解。
3.推广结论
推广结论为︰在一个电压源阻容串联回路中,如果从以任何一个电容两端电压为输出,那么它一定是一个低通电路,其上限截止频率为1/2ΠRC,其中R为回路中所有电阻之和,C为回路中所有电容的串联值(类似于电阻并联计算)。
小结
提示:这里可以添加总结
如果它们的上限截止频率相差不大,或者干脆三个值相等,则情况会变得复杂。理论上说,第一要考虑各级串联时的相互影响,第二要写传函精细分析。但是,我们不希望在这个阶段就让大家陷入到复杂的数学推导中,一个简化的公式和表格可以帮助我们。
将一个低通模块和高通模块串联,哪个在前哪个在后,结果是一样的。如果f仲f,则最终表现为一个带通环节,它的中频增益为两者增益的乘积,它同时具有上限截止频率和下限截止频率,当两者相差甚远时,它们是独立的,互不影响,如果fu<ft,则表现为一个全频段阻断状态,一般没有人这么干。






![[进阶]网络通信:TCP通信-支持与多个客户端同时通信](https://img-blog.csdnimg.cn/2b6c444834844ac1a56f08abeece00a8.png)