29基于贝叶斯（Bayes）判别的机场航班延误因素分析(附matlab程序)

news2024/9/21 2:30:18

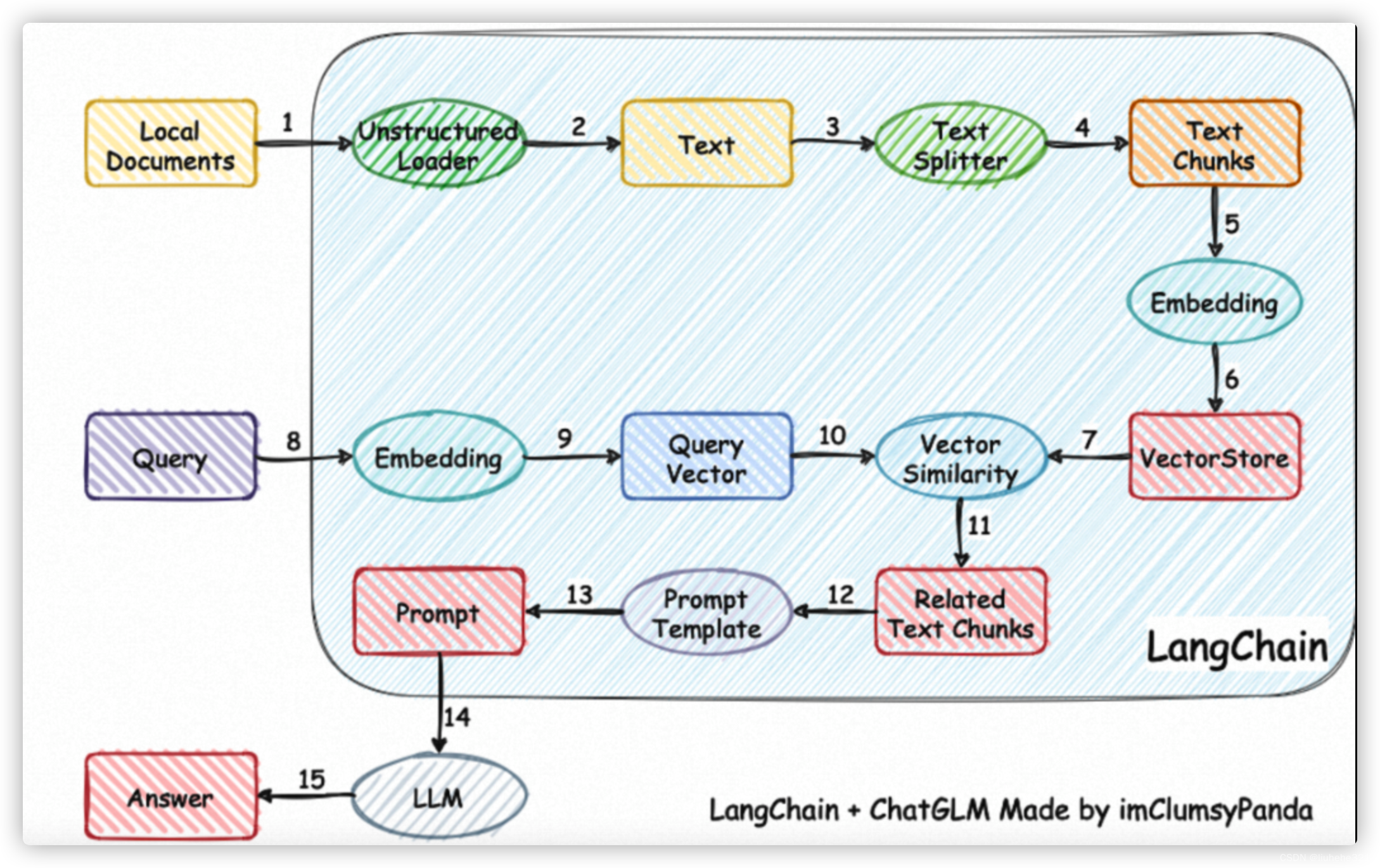
1.简述

学习目标：基于贝叶斯判别的机场航班延误因素分析

利用所创建的朴素贝叶斯分类器对象ObjBayes，对训练样本进行判别

并利用贝叶斯预测误差统计

中国民航业近年来快速发展,航班量增多,航班密度逐步加大,许多资源配置的矛盾也日益凸显出来.机场大面积航班延误难以避免.针对上述问题,在航班延误波及分析的基础上,建立机场航班延误的贝叶斯网络分析模型.通过机场航班数据网络学习和测试,得到了不同因素对机场航班延误的影响程度,不同时间段的延误情况,为机场当局解决大面积航班延误提供决策依据.

关键词：

在网络上介绍贝叶斯定理，贝叶斯网格的资料随处可见，我在此处就简单给大家的阐述一下什么是贝叶斯，贝叶斯方法其实在高中的时候我们就已经开始接触了，高中的概率大部分讲述的就是贝叶斯方法。

其实在贝叶斯方法真正的被人们认可之前，频率派是概率的主导，假设又一袋球，里面有若干红球和黑球，在贝叶斯之前你随便问一个人拿出红球的概率是多少，他会说50%。嘿！懵逼不？没有黑球红球的数量怎么知道的50%，频率派中的思考方式是不是红球就是黑球，所以50%。

贝叶斯方法的提出

托马斯·贝叶斯Thomas Bayes（1702-1763）在世时，并不为当时的人们所熟知，很少发表论文或出版著作，与当时学术界的人沟通交流也很少，用现在的话来说，贝叶斯就是活生生一民间学术“屌丝”，可这个“屌丝”最终发表了一篇名为“An essay towards solving a problem in the doctrine of chances”，翻译过来则是：机遇理论中一个问题的解。你可能觉得我要说：这篇论文的发表随机产生轰动效应，从而奠定贝叶斯在学术史上的地位。

首先声明，概率确确实实是一个不确定的值，因为既然叫概率，就包含有运气的成分，假设以一个朋友创业来说，创业无非成功与失败两种结果，依照频率论的方式，他成功就是50%。但是你了解他的为人，他有想法，有思路，有毅力，所以你可能认为他成功的概率为70%，这就是贝叶斯的思考方式。他区别于传统频率派的非黑即白，加入了前提。

贝叶斯定理

在讲述贝叶斯定理之前，先介绍几个定义

1）条件概率（后验概率）就是事件A在另一个事件B已经发生的条件下发生概率，公式表示为P(A|B)，读作“在B条件下A的概率”。

2）联合概率表示两件事情共同发生的概率。A与B的联合概率表示为p(A,B).

3）边缘概率（又称先验概率）是某个事件发生的概率。边缘概率是这样得到的：在联合概率中，把最终结果中那些不需要的事件通过合并成它们的全概率，而消去它们（对离散随机变量用求和得全概率，对连续随机变量用积分得全概率），这称为边缘化（marginalization），比如A的边缘概率表示为P(A)，B的边缘概率表示为P(B)。

贝叶斯网络的定义

贝叶斯网络又称信度网络，是Bayes方法的扩展，是目前不确定知识表达和推理领域最有效的理论模型之一。从1988年由Pearl提出后，已经成为近几年来研究的热点.。一个贝叶斯网络是一个有向无环图(Directed Acyclic Graph,DAG),由代表变量结点及连接这些结点有向边构成。结点代表随机变量，结点间的有向边代表了结点间的互相关系(由父结点指向其子结点)，用条件概率进行表达关系强度，没有父结点的用先验概率进行信息表达。结点变量可以是任何问题的抽象，如：测试值，观测现象，意见征询等。适用于表达和分析不确定性和概率性的事件，应用于有条件地依赖多种控制因素的决策，可以从不完全、不精确或不确定的知识或信息中做出推理。

2.代码

clc,clear,close all
load('sourcedata.mat');
load data.mat
load('datatest.mat');
n=size(data);

%% 创建朴素贝叶斯分类器对象
%% 创建朴素贝叶斯分类器对象ObjBayes
training=data(1:103,1:5);
group=data(1:103,6);
ObjBayes = NaiveBayes.fit(training,group,'Distribution','kernel')
%% 对训练样本进行判别
%% 利用所创建的朴素贝叶斯分类器对象ObjBayes，对训练样本进行判别
pre0 = ObjBayes.predict(training);
disp '贝叶斯分类器训练数据和实际结果是否相等，相等为1，否则为0'
isequal(pre0, group) % 判断判别结果pre0与分组向量group是否相等

pre1 = ObjBayes.predict(data(1:103,1:5));

figure,
subplot(211),bar(data(:,6));figure(gcf);axis tight,box off,grid on
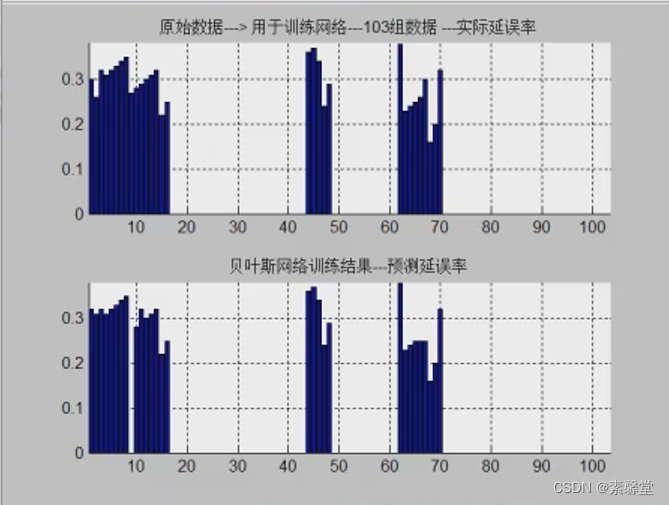
title('原始数据---> 用于训练网络---103组数据 ---实际延误率')
subplot(212),bar(pre1);figure(gcf);axis tight,box off,grid on
title('贝叶斯网络训练结果---预测延误率')

%% 贝叶斯预测误差统计
By1=ysw(data,pre1)

%%
%% 对于样本进行预测
test=datatest(:,1:5);
datatestresult=datatest(:,6);
pre2 = ObjBayes.predict(test);
figure,

subplot(211),bar(datatest(:,6));figure(gcf);axis tight,box off,grid on
title('输入待检验的数据，实际结果')
subplot(212),bar(pre2);figure(gcf);axis tight,box off,grid on
title('贝叶斯网络训练结果')

%% 贝叶斯预测误差统计
By2=ysw(datatest,pre2)

3.运行结果