BM算法(Boyer-Moore)

BM算法也叫做精确字符集算法，它是一种从右往左比较（后往前），同时也应用到了两种规则坏字符、好后缀规则去计算我们移动的偏移量的算法。

坏字符规则

BM 算法是从后往前进行比较，此时我们发现比较的第一个字符就不匹配，我们将主串这个字符称之为坏字符，也就是 f 。我们发现坏字符之后，模式串 T 中查找是否含有该字符（f），我们发现并不存在 f，此时我们只需将模式串右移到坏字符的后面一位即可。如下图：

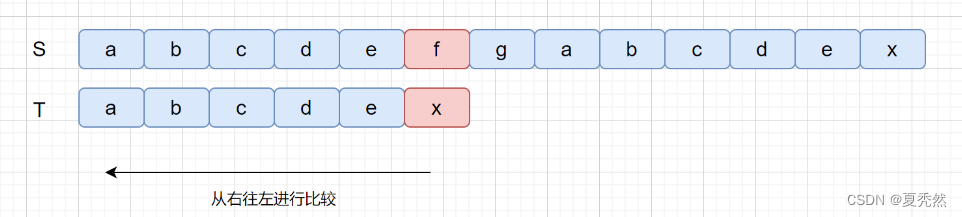
BM 算法是从后往前进行比较，此时我们发现比较的第一个字符就不匹配，我们将主串这个字符称之为坏字符，也就是 f ，我们发现坏字符之后，模式串 T 中查找是否含有该字符（f），我们发现并不存在 f，此时我们只需将模式串右移到坏字符的后面一位即可。如下图：

那我们在模式串中找到坏字符该怎么办呢？

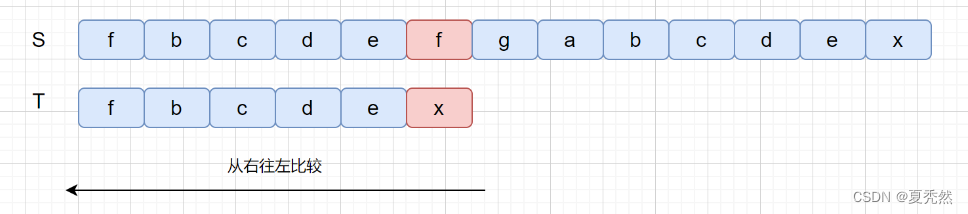
此时我们的坏字符为 f ,我们在模式串中，查找发现含有坏字符 f,我们则需要移动模式串 T ,将模式串中的 f 和坏字符对齐。见下图：

然后我们继续从右往左进行比较，发现 d 为坏字符，则需要将模式串中的 d 和坏字符对齐。

那么我们在来思考一下这种情况，那就是模式串中含有多个坏字符怎么办呢？

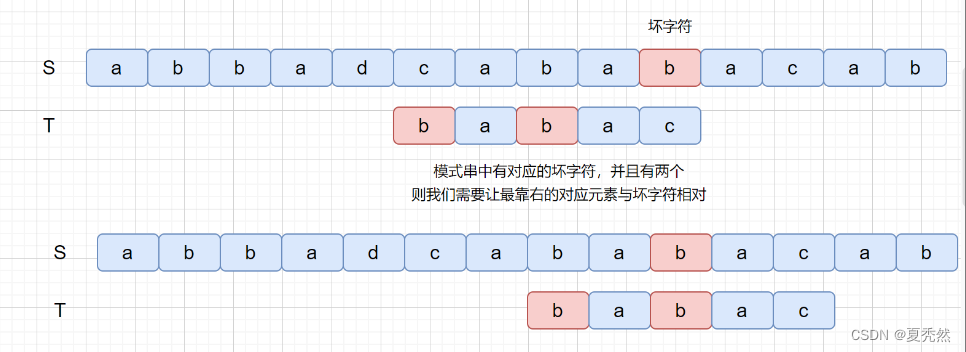
那么我们为什么要让最靠右的对应元素与坏字符匹配呢？如果上面的例子我们没有按照这条规则看下会产生什么问题。

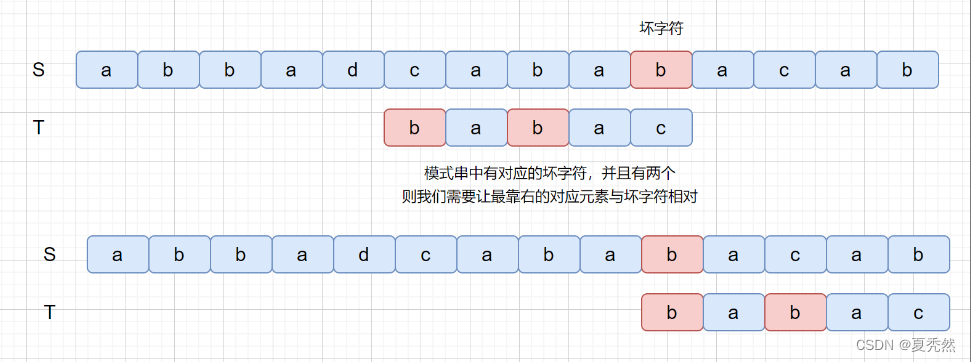
如果没有按照我们上述规则，则会漏掉我们的真正匹配。我们的主串中是含有 babac 的，但是却没有匹配成功，所以应该遵守最靠右的对应字符与坏字符相对的规则。

我们上面一共介绍了三种移动情况，分别是下方的模式串中没有发现与坏字符对应的字符，发现一个对应字符，发现两个。这三种情况我们分别移动不同的位数，那我们是根据依据什么来决定移动位数的呢？下面我们给图中的字符加上下标。见下图：

下面我们来考虑一下这种情况。

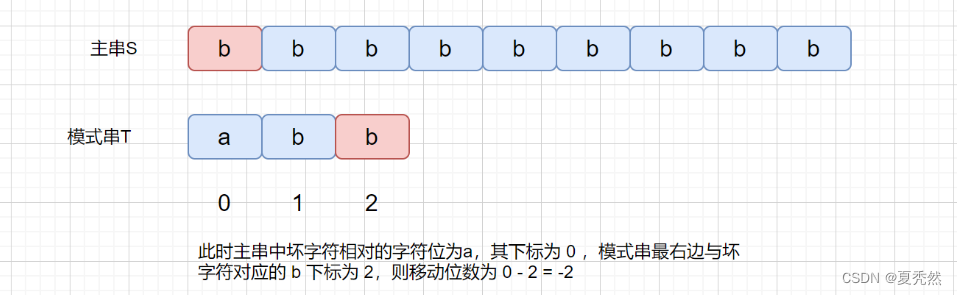
此时这种情况肯定是不行的，不往右移动，甚至还有可能左移，那么我们有没有什么办法解决这个问题呢？继续往下看吧。

好后缀规则

好后缀其实也很容易理解，我们之前说过 BM 算法是从右往左进行比较，下面我们来看下面这个例子。

这里如果我们按照坏字符进行移动是不合理的，这时我们可以使用好后缀规则，那么什么是好后缀呢？

BM 算法是从右往左进行比较，发现坏字符的时候此时 cac 已经匹配成功，在红色阴影处发现坏字符。此时已经匹配成功的 cac 则为我们的好后缀，此时我们拿它在模式串中查找，如果找到了另一个和好后缀相匹配的串，那我们就将另一个和好后缀相匹配的串 ，滑到和好后缀对齐的位置。

是不是感觉有点拗口，没关系，我们看下图，红色代表坏字符，绿色代表好后缀。

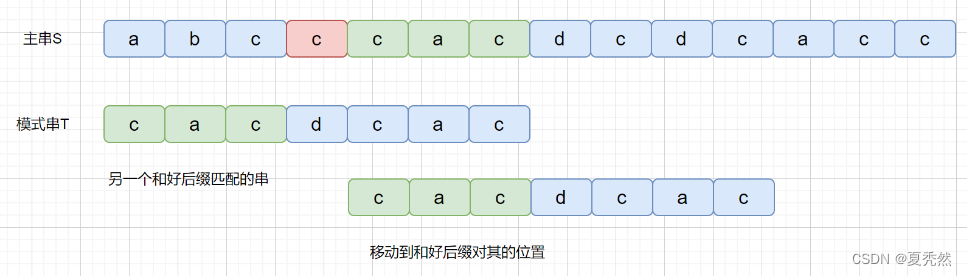
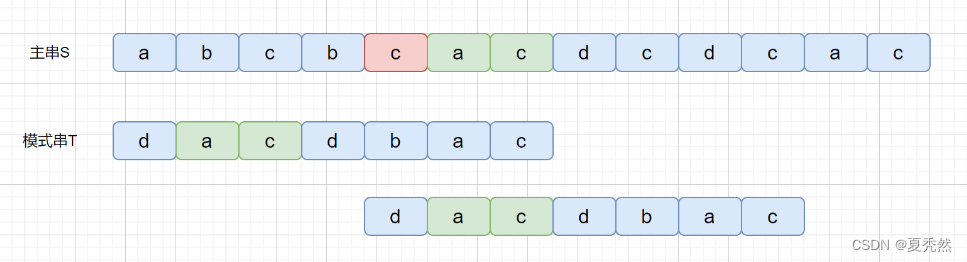
上面那种情况搞懂了，但是我们思考一下下面这种情况。

上面我们说到了，如果在模式串的头部没有发现好后缀，发现好后缀的子串也可以。但是为什么要强调这个头部呢？

我们下面来看一下这种情况。

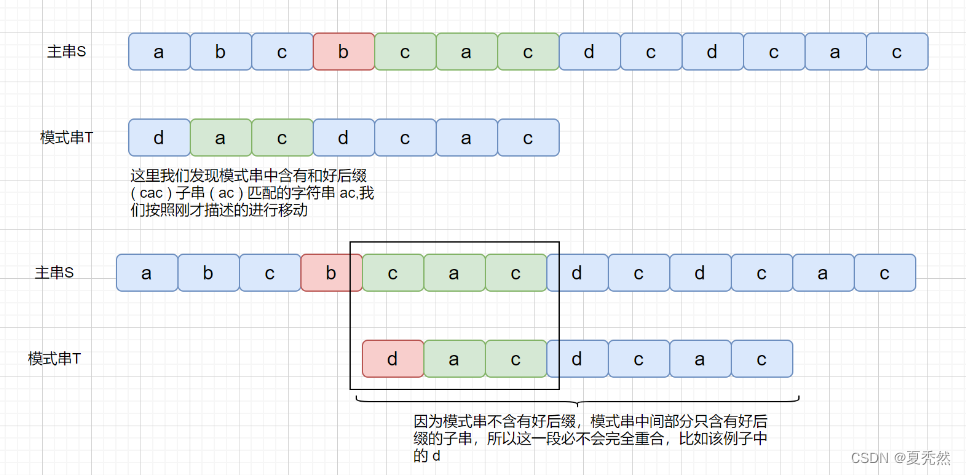
但是当我们在头部发现好后缀的子串时，是什么情况呢？

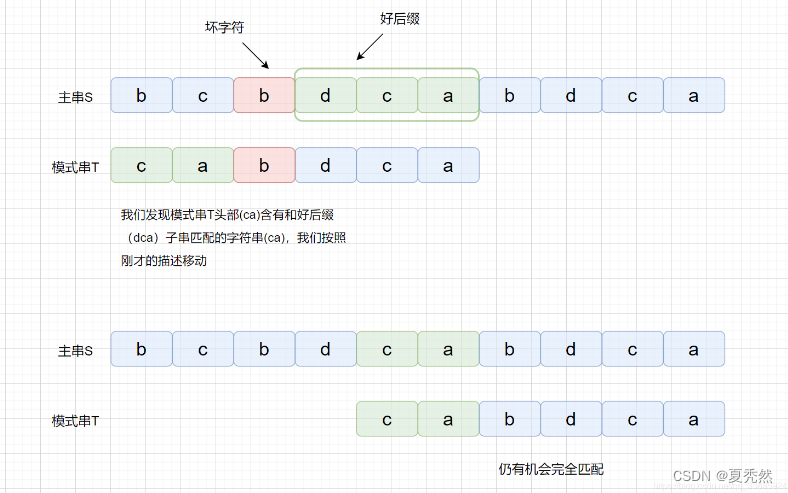
说到这里，坏字符和好后缀规则就算说完了，坏字符很容易理解，我们对好后缀总结一下：

1. 如果模式串含有好后缀，无论是中间还是头部可以按照规则进行移动。如果好后缀在模式串中出现多次，则以最右侧的好后缀为基准。
2. 如果模式串头部含有好后缀子串则可以按照规则进行移动，中间部分含有好后缀子串则不可以。
3. 如果在模式串尾部就出现不匹配的情况，即不存在好后缀时，则根据坏字符进行移动，这里有的文章没有提到，是个需要特别注意的地方。

之前我们刚开始说坏字符的时候，是不是有可能会出现负值的情况 （存在好后缀的情况才有可能出现负值），即往左移动的情况，所以我们为了解决这个问题，我们可以分别计算好后缀和坏字符往后滑动的位数 （好后缀不为 0 的情况），然后取两个数中最大的，作为模式串往后滑动的位数。

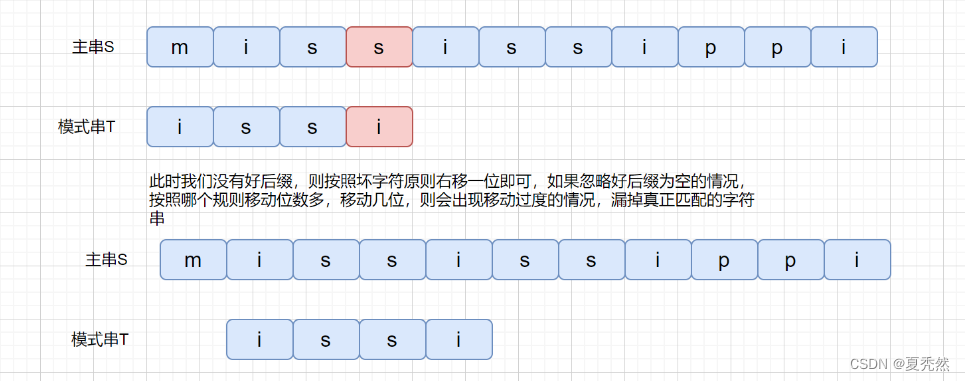
实现过程

在构建坏字符移动位数表的时候，因为只需要对整个模式串进行一次循环，所以速度是很快的，时间复杂度为$O(m)$，代码如下：

# 用来求坏字符情况下移动位数
def badChar(self, t, t_len):
	# 初始化
    bc_dict = dict()
    # t_len 代表模式串的长度，如果有两个字符'a',则后面那个会覆盖前面那个的位置
    # 因此可以保证最终得到的是字符在模式串中的最后一个位置
    for i in range(t_len):
        bc_dict[t[i]] = i
    return bc_dict 

在构建好后缀移动位数表的时候，通常容易想到的方法是：首先需要定义一个数组用来存储移动位数，之后依次增长后缀长度，每次选定后缀都需要遍历查询有无匹配的后缀，以及位于模式串头的后缀子串。算法时间复杂度 $O(n^3)$（两个for加一个==），代码如下：

# 构建好后缀规则移动字典
def good_suffix(self, t, t_len):
    gs_list = [t_len] * t_len
    for i in range(1, t_len):
        suffix = t[i:]
        suffix_len = t_len - i
        for j in range(t_len-1, -suffix_len, -1):
            if j >= suffix_len:
                if t[j-suffix_len: j] == suffix:
                    gs_list[t_len-i] = t_len - j
                    break 
            else:
                if t[0: j] == suffix[suffix_len-j:]:
                    gs_list[t_len-i] = t_len - j
                    break 
    return gs_list

由于 $O(n^3)$ 的时间复杂度太慢了，于是有一种很巧妙的算法，算法时间复杂度 $O(n^2)$。

他的思路是构建两个数组来进行优化，其中一个是好后缀在模式串中出现的最后一个的位置数组 suffix（不包含好后缀子串的情况），另外一个数组 prefix 是对应于 suffix 的，记录着其是否位于模式串头部，如下图：

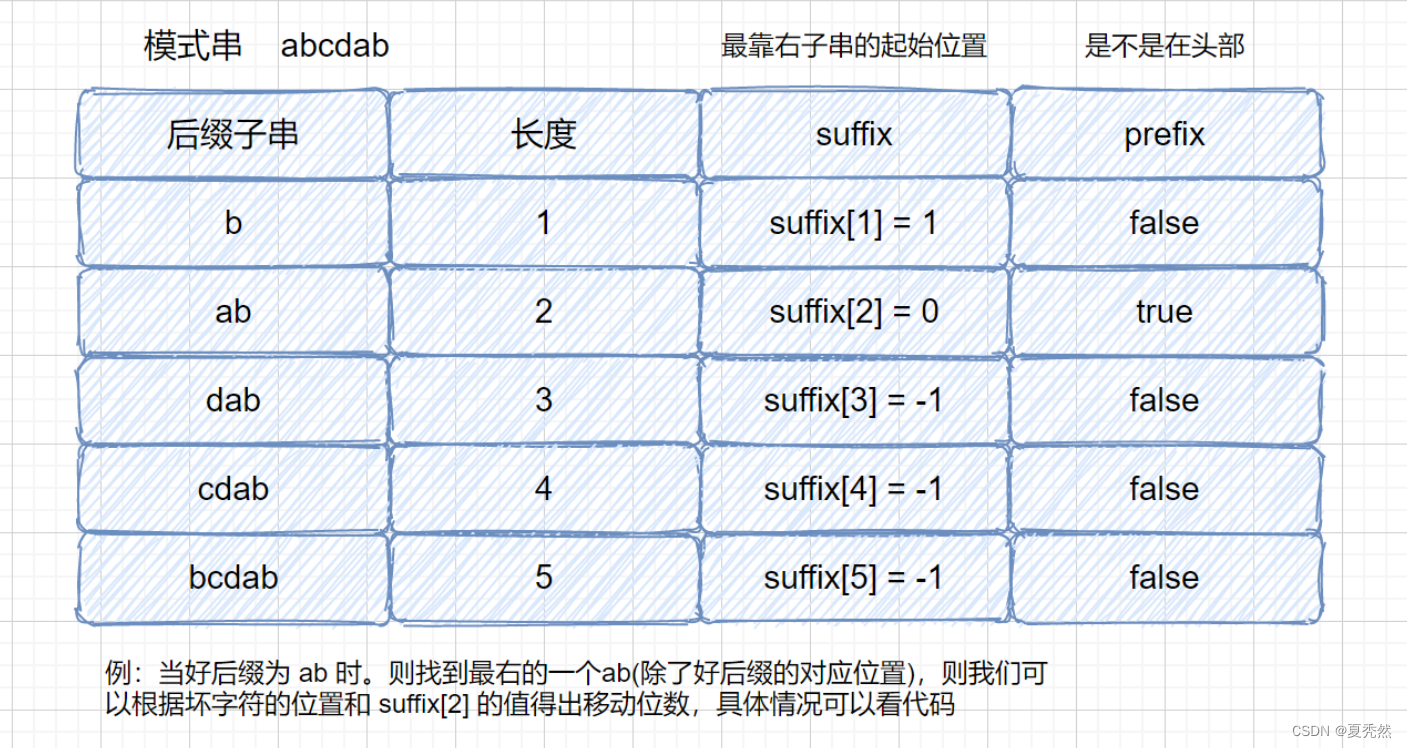
代码如下：

# 用来求辅助数组 suffix 和 prefix
def goodSuffix(self, t, t_len):
	# 初始化
    suffix = [-1] * t_len
    prefix = [False] * t_len
    # 递增子串长度，直到 t_len-1，从 0 开始可以从远到近依次覆盖得到最优 suffix
    for i in range(t_len-1):
        start = i
        suffix_length = 0
        # 更新 suffix 数组，分别从取子串和模式串倒数第一个值开始
        # 如果相等且子串长度不为 0，则令 suffix[suffix_length] = start，
        # 其中suffix_length为后缀长度，start 等同于模式串中与后缀相同的字符串所处的位置
        while start >= 0 and t[start] == t[t_len-1-suffix_length]:
            suffix_length += 1
            suffix[suffix_length] = start
            start -= 1
        # 更新prefix数组，等于-1说明已经遍历完字符串头部
        if start == -1:
            prefix[suffix_length] = True
    return suffix, prefix

得到两个数组之后，即可通过坏字符的下标获取到好后缀的移动位数，步骤为：

1. 获取好后缀长度
2. 判断 suffix 数组中如果含有长度为 suffix_length 的好后缀，返回移动位数
3. 找头部为好后缀子串的最大长度，从长度最大的子串开始，如果是头部，则移动 t_len - k 个位数
4. 如果没有发现 好后缀匹配的串/头部为好后缀子串，则移动到 t_len 位，也就是模式串的长度

# 根据 suffix 和 prefix 以及坏字符的下标获取到好后缀的移动位数
def move(self, i, t_len, suffix, prefix):
	# i代表坏字符的下标
    # 好后缀长度
    suffix_length = t_len - 1 - i
    # 如果含有长度为 suffix_length 的好后缀，返回移动位数
    if suffix[suffix_length] != -1:
        return i + 1 - suffix[suffix_length]
    # 找头部为好后缀子串的最大长度，从长度最大的子串开始
    for k in range(suffix_length-1, 0, -1):
        # 如果是头部，则移动 t_len - k 个位数
        if prefix[k] is True:
            return t_len - k
    # 如果没有发现 好后缀匹配的串/头部为好后缀子串，则移动到 t_len 位，也就是模式串的长度
    return t_len

已经完成坏字符和好后缀所需要的函数，下面可以进行对BM算法的搜索流程进行实现：

1. 获取坏字符移动位数表以及suffix, prefix数组
2. 模式串搜索：（从第一个字符开始匹配）：
   • 如果匹配字符的位置大于两字符长度的差值，则不可能存在匹配字串，故退出循环，返回 -1
   • 如果未达到，则从后往前匹配：
     1. 匹配成功，返回当前下标
     2. 匹配失败，找到坏字符，并计算需要移动的位数：
        • 如果不含有好后缀的话：
          1. 求出坏字符规则下移动的位数，将当前下标进行移动。
        • 如果有好后缀的话：
          1. 求出坏字符规则下移动的位数
          2. 求出好后缀情况下的移动位数
          3. 当前下标选择两种规则的最大偏移位数进行移动
          4. 按照新的下标重新开始模式串搜索

注意：步骤中好后缀情况下的移动位数存在重复计算，故可以采用额外空间存储已经计算过的值对时间复杂度进行优化。

def bm(self, s, s_len, t, t_len):
   		# 获取好后缀移动位数表
        bc_dict = self.badChar(t, t_len)
        # suffix 用来保存各种长度好后缀的最右位置的数组
        # prefix 判断是否是头部，如果是头部则true
        suffix, prefix = self.goodSuffix(t, t_len)
        # 用来存储已经查询过的好后缀移动位数，可减少时间开销（优化点）
        gs_dict = [None] * t_len
        # 第一个匹配字符
        now = 0
        # 如果匹配字符的位置到达两字符长度的差值，则不可能存在匹配字串，则退出循环
        while now <= s_len - t_len:
            i = t_len - 1
            # 从后往前匹配，匹配失败，找到坏字符
            while i >= 0 and s[now+i] == t[i]:
                i -= 1
            # 退出条件，模式串遍历完毕，匹配成功，返回当前下标 now
            if i < 0:
                return now
            # 下面为匹配失败时，如何处理
            # 求出坏字符规则下移动的位数，就是我们坏字符下标减最右边的下标
            bc_move = i - bc_dict.get(s[now+i], -1)
            gs_move = 0 
            # 好后缀情况，求出好后缀情况下的移动位数,如果不含有好后缀的话，则按照坏字符来
            if t_len - 1 > 0 and t_len - 1 > i:
                # 判断是否计算过，如果没有计算过则需要计算后存储答案至列表
                if gs_dict[i] is None:
                    gs_dict[i] = self.move(i, t_len, suffix, prefix)
                gs_move = gs_dict[i]
            # 选择最大偏移位数进行移动
            now += max(bc_move, gs_move)
        return -1

完整代码

class Solution:
    
    def strStr(self, haystack: str, needle: str) -> int:
        haystack_length = len(haystack)
        needle_length = len(needle)
        return self.bm(haystack, haystack_length, needle, needle_length)
        
    def bm(self, s, s_len, t, t_len):
   		# 获取好后缀移动位数表
        bc_dict = self.badChar(t, t_len)
        # suffix 用来保存各种长度好后缀的最右位置的数组
        # prefix 判断是否是头部，如果是头部则true
        suffix, prefix = self.goodSuffix(t, t_len)
        # 用来存储已经查询过的好后缀移动位数，可减少时间开销（优化点）
        gs_dict = [None] * t_len
        # 第一个匹配字符
        now = 0
        # 如果匹配字符的位置到达两字符长度的差值，则不可能存在匹配字串，则退出循环
        while now <= s_len - t_len:
            i = t_len - 1
            # 从后往前匹配，匹配失败，找到坏字符
            while i >= 0 and s[now+i] == t[i]:
                i -= 1
            # 退出条件，模式串遍历完毕，匹配成功，返回当前下标 now
            if i < 0:
                return now
            # 下面为匹配失败时，如何处理
            # 求出坏字符规则下移动的位数，就是我们坏字符下标减最右边的下标
            bc_move = i - bc_dict.get(s[now+i], -1)
            gs_move = 0 
            # 好后缀情况，求出好后缀情况下的移动位数,如果不含有好后缀的话，则按照坏字符来
            if t_len - 1 > 0 and t_len - 1 > i:
                # 判断是否计算过，如果没有计算过则需要计算后存储答案至列表
                if gs_dict[i] is None:
                    gs_dict[i] = self.move(i, t_len, suffix, prefix)
                gs_move = gs_dict[i]
            # 选择最大偏移位数进行移动
            now += max(bc_move, gs_move)
        return -1
        
    # 根据 suffix 和 prefix 以及坏字符的下标获取到好后缀的移动位数
    def move(self, i, t_len, suffix, prefix):
        # i代表坏字符的下标
        # 好后缀长度
        suffix_length = t_len - 1 - i
        # 如果含有长度为 suffix_length 的好后缀，返回移动位数
        if suffix[suffix_length] != -1:
            return i + 1 - suffix[suffix_length]
        # 找头部为好后缀子串的最大长度，从长度最大的子串开始
        for k in range(suffix_length-1, 0, -1):
            # 如果是头部，则移动 t_len - k 个位数
            if prefix[k] is True:
                return t_len - k
        # 如果没有发现 好后缀匹配的串/头部为好后缀子串，则移动到 t_len 位，也就是模式串的长度
        return t_len

    # 用来求坏字符情况下移动位数
    def badChar(self, t, t_len):
        # 初始化
        bc_dict = dict()
        # t_len 代表模式串的长度，如果有两个字符'a',则后面那个会覆盖前面那个的位置
        # 因此可以保证最终得到的是字符在模式串中的最后一个位置
        for i in range(t_len):
            bc_dict[t[i]] = i
        return bc_dict 
    
    # 用来求辅助数组 suffix 和 prefix
    def goodSuffix(self, t, t_len):
        # 初始化
        suffix = [-1] * t_len
        prefix = [False] * t_len
        # 递增子串长度，直到 t_len-1，从 0 开始可以从远到近依次覆盖得到最优 suffix
        for i in range(t_len-1):
            start = i
            suffix_length = 0
            # 更新 suffix 数组，分别从取子串和模式串倒数第一个值开始
            # 如果相等且子串长度不为 0，则令 suffix[suffix_length] = start，
            # 其中suffix_length为后缀长度，start 等同于模式串中与后缀相同的字符串所处的位置
            while start >= 0 and t[start] == t[t_len-1-suffix_length]:
                suffix_length += 1
                suffix[suffix_length] = start
                start -= 1
            # 更新prefix数组，等于-1说明已经遍历完字符串头部
            if start == -1:
                prefix[suffix_length] = True
        return suffix, prefix

总结

BM算法很好地利用了后缀的匹配方式，是很优秀的单模匹配算法，但是BM算法构建好后缀表需要花大量的时间，往往对于小规模匹配情况可能KMP算法和C标准函数strstr效果更好（strstr函数虽然用的是O(n^2)的算法，但是可能模式串也不是很大，而且这个函数可能是经过微软在汇编层进行过优化的。）

文章参考

《BM算法和Sunday快速字符串匹配算法》（代码实现部分借鉴大部分来自于此！！！）
《这可能是全网最细的 KMP 讲解！(BF,BM,KMP）》(理论部分借鉴大部分来自于此！！！)