前言

今天开始我将陆续为大家更新面试经典150题中较难理解的题目。今天我为大家分享的是，除自身以外数组的乘积、跳跃游戏| 和 跳跃游戏||。

除自身以外数组的乘积

除自身以外数组的乘积

要求

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请不要使用除法，且在 O(n) 时间复杂度内完成此题

示例 1:

输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:

输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

class Solution {
    public int[] productExceptSelf(int[] nums) {

    }
}

思路

按照一般的思路，我们可能会想：先将数组中所有的元素相乘得到一个sum，然后再遍历一遍数组，answer[i] = sum / nums[i]，如果nums[i] = 0，answer[i] = sum。但是这个题目要求我们不使用除法，那么我们该怎么办呢？因为是除自身以外的数组的乘积，自身以外的数组被分为左右两部分，我们只需要将 左边部分数组元素的乘积 x 右边部分数组元素的乘积 就得到除自身以外的数组的乘积。所以我们可以使用两个数组L和R来分别存储数组第 i 个元素左边部分数组元素的乘积和右边部分数组元素的乘积，最后再遍历一遍数组，answer[i] = L[i] * R[i]。

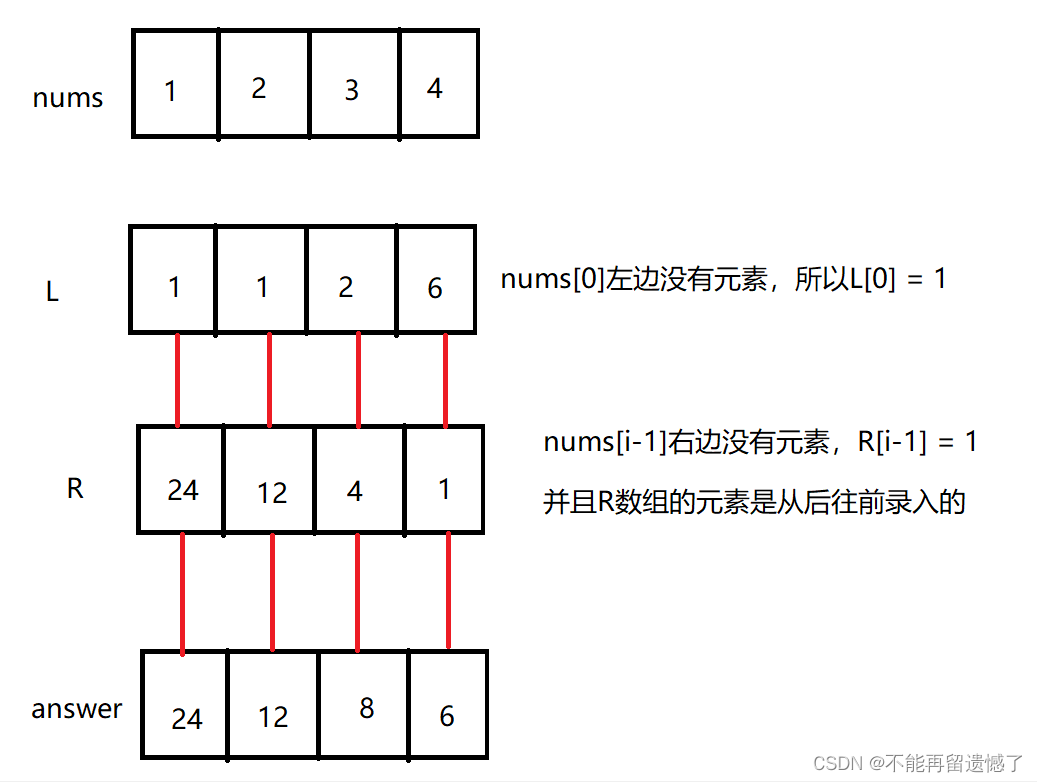
代码

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int n = nums.length;
        int[] answer = new int[n];
        int[] L = new int[n];
        int[] R = new int[n];
        L[0] = 1;
        for(int i = 1; i < n; i++) {
        //L[i]等于前i-2个数的乘积乘上第i-1个数
            L[i] = L[i-1] * nums[i-1];
        } 
        R[n-1] = 1;
        for(int i = n - 2; i >= 0; i--) {
        //R[i]等于后 length-i-2 个数的乘积乘上第 length-i-1个数
            R[i] = R[i+1] * nums[i+1];
        }

        for(int i = 0; i < n; i++) {
            answer[i] = L[i] * R[i];
        }

        return answer;
    }
}

跳跃游戏|

跳跃游戏|

要求

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

class Solution {
    public int jump(int[] nums) {

    }
}

题解

其实这个题目可以换一种理解方式：在某位置的跳跃范围内时候有某一位置可以跳跃到最后一个下标处。我们可以使用 rightmost 来记录在某位置的跳跃范围内的最大跳跃位置， 最大跳跃位置 = i + nums[i] 如果 rightmost >= length-1，那么说明可以到达最后一个下标处。

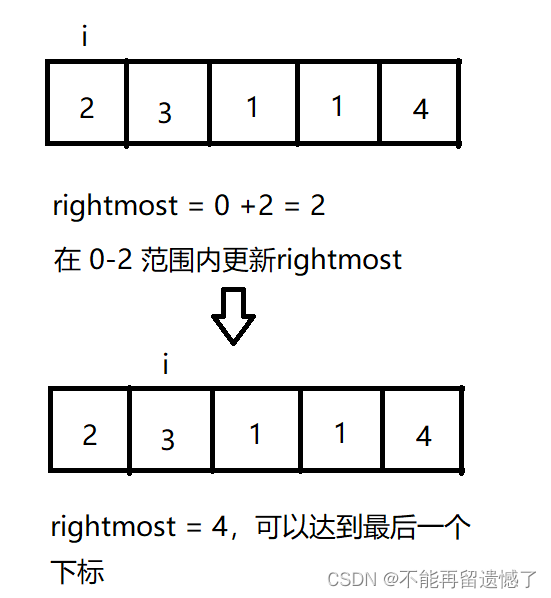
代码

class Solution {
    public boolean canJump(int[] nums) {
        int n = nums.length;
        int rightmost = 0;
        for(int i = 0; i < n; i++) {
            if(i <= rightmost) {
                rightmost = Math.max(rightmost,i + nums[i]);
                if(rightmost >= n-1) {
                    return true;
                }
            }
        }
        return false;
    }
}

跳跃游戏||

跳跃游戏||

要求

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。
示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

class Solution {
    public int jump(int[] nums) {

    }
}

题解

因为题目中说生成的测试用例可以到达nums[i-1]，求最小的跳跃次数。所以我们每次跳跃的位置就是在跳跃区间中能跳跃最远的位置。并且在遍历数组时，我们不访问最后一个元素，这是因为在访问最后一个元素之前，我们的边界一定大于等于最后一个位置，否则就无法跳到最后一个位置了。如果访问最后一个元素，在边界正好为最后一个位置的情况下，我们会增加一次「不必要的跳跃次数」，因此我们不必访问最后一个元素。

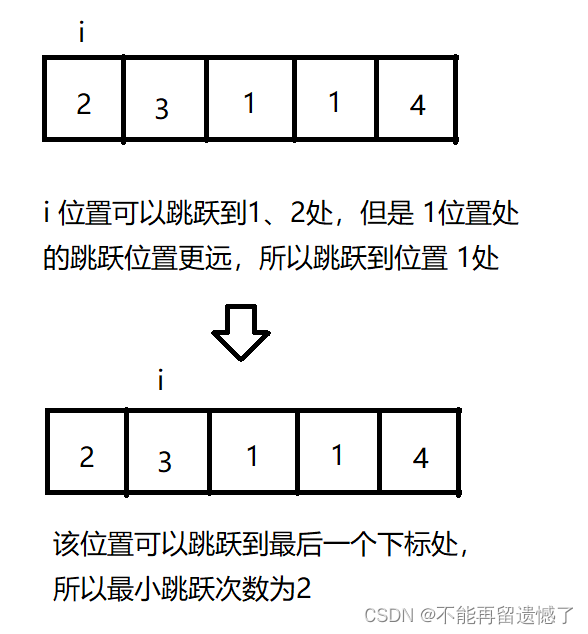
代码

class Solution {
    public int jump(int[] nums) {
        int n = nums.length;
        int rightmost = 0;
        //end用来记录跳跃区间
        int end = 0;
        int step = 0;
        for(int i = 0; i < n - 1; i++) {
            rightmost = Math.max(rightmost,i + nums[i]);
            if(i == end) {
                end = rightmost;
                step++;
            }
        }

        return step;
    }
}