动手学强化学习：多臂老虎机问题

强化学习思维导图
简介
问题介绍
- 问题定义
- 形式化描述
- 累积懊悔
- 估计期望奖励
贪心策略与 $\epsilon$ -greedy策略
上置信界算法
汤普森采样算法
参考资料

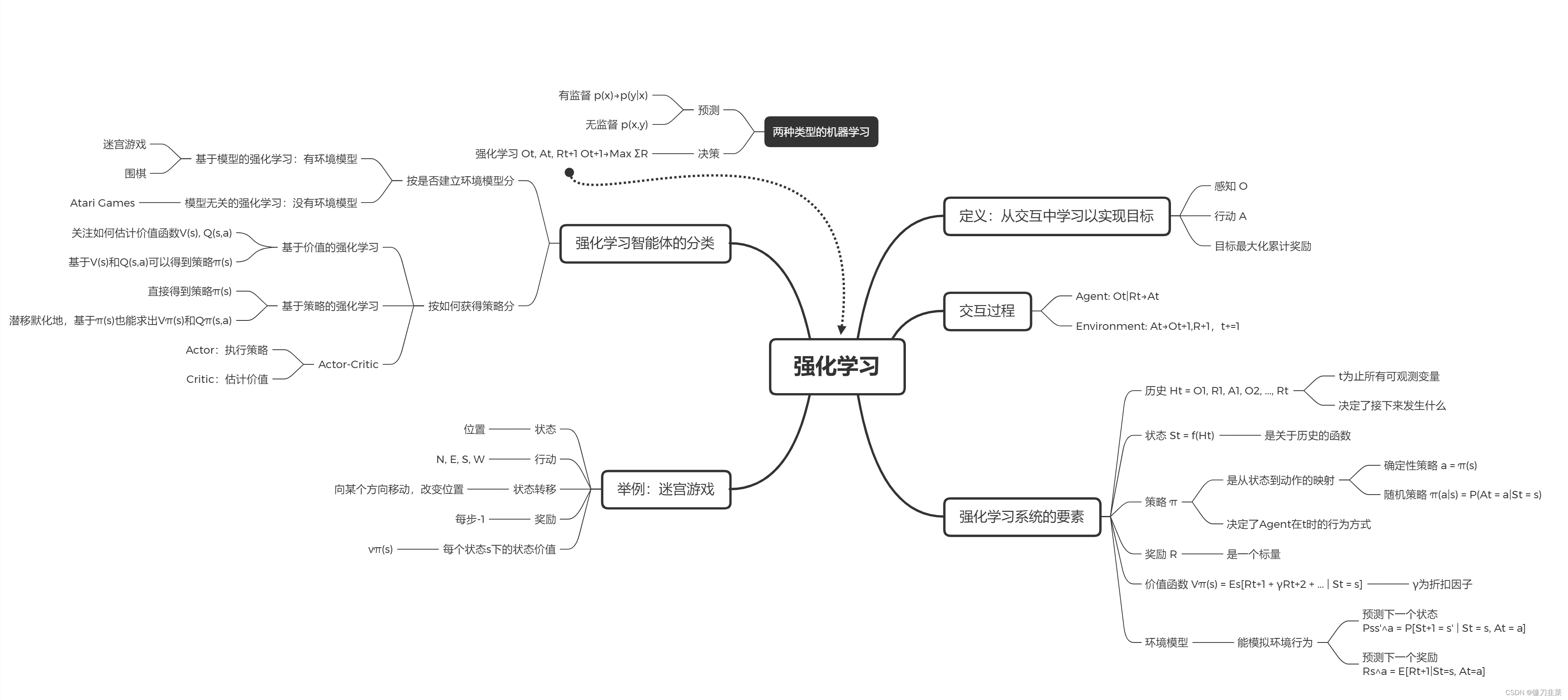
强化学习思维导图

强化学习

简介

强化学习关注智能体和环境交互过程中的学习，这是一种试错型学习（trial-and-error learning）范式。在正式学习强化学习之前，我们需要先了解多臂老虎机问题，它可以被看作简化版的强化学习问题。与强化学习不同，多臂老虎机不存在状态信息，只有动作和奖励，算是最简单的“和环境交互中的学习”的一种形式。多臂老虎机中的探索与利用（exploration vs. exploitation）问题一直以来都是一个特别经典的问题，理解它能够帮助我们学习强化学习。

Exploitation执行能够获得已知最优收益的决策
Exploration尝试更多可能的决策，不一定会是最优收益

形式化序列决策问题如下：

探索：可能发现更好的策略
探索与利用

问题介绍

问题定义

在多臂老虎机（multi-armed bandit，MAB）问题（见图 2-1）中，有一个拥有K根拉杆的老虎机，拉动每一根拉杆都对应一个关于奖励的概率分布R。我们每次拉动其中一根拉杆，就可以从该拉杆对应的奖励概率分布中获得一个奖励r。我们在各根拉杆的奖励概率分布未知的情况下，从头开始尝试，目标是在操作T次拉杆后获得尽可能高的累积奖励。由于奖励的概率分布是未知的，因此我们需要在“探索拉杆的获奖概率”和“根据经验选择获奖最多的拉杆”中进行权衡。“采用怎样的操作策略才能使获得的累积奖励最高”便是多臂老虎机问题。

形式化描述

多臂老虎机问题是概率论中一个经典问题，也属于强化学习的范畴。设想，一个赌徒面前有N个老虎机，事先他不知道每台老虎机的真实盈利情况，他如何根据每次玩老虎机的结果来选择下次拉哪台或者是否停止赌博，来最大化自己的从头到尾的收益。

多臂老虎机问题可以表示为一个元组<A,R>，其中：

A为动作集合，其中一个动作表示拉动一个拉杆。如果多臂老虎机一共有K跟拉杆，那么动作空间就是集合 ${a_1,...,a_K\}$ ，用 $a_t\in A$ 表示任意一个动作；
R为奖励概率分布，拉动每一根拉杆的动作 $a$ 都对应一个奖励概率分布 $R (r ∣ a)$ ，不同拉杆的奖励分布通常是不同的。

假设每个时间步只能拉动一根拉杆，多臂老虎机的目标为最大化一段时间步T内累积的奖励： $\sum_{t=1}^T{r_t,r_t\in R(\cdot|a_t)}$ ，其中 $a_t$ 表示在 $t$ 时间步拉动某一拉杆的动作， $r_t$ 表示动作 $a_t$ 的奖励。

在商业中，多臂老虎机问题有着广泛的应用，包括广告展示、医学试验和金融等领域。比如在推荐系统中，我们有N个物品，事先不知道用户U对N个物品的反应，我们需要每次推荐给用户某个物品，来最大化用户的价值(或者说尽量使得用户U转化)，比如用户的购买。

累积懊悔

对于每一个动作 $a$ ，我们定义其期望奖励为 $Q(a^i)=\mathbb{E}_{r \sim \mathcal{R}(r\mid a^i)}[r|a^i]$ 。于是，至少存在一根拉杆，它的期望奖励不小于拉动其他任意一根拉杆，我们将该最优期望奖励表示为 $Q^{*}=\max _{a^i \in \mathcal{A}} Q(a^i)$ 。为了更加直观、方便地观察拉动一根拉杆的期望奖励离最优拉杆期玍奖励的差距，我们引入懊悔 (regret) 概念。懊悔定义为拉动当前拉杆的动作 $a$ 与最优拉杆的期望奖励差，即 $R(a^i)=Q^{*}-Q(a^i)$ 。累积懊悔 (cumulative regret) 即操作 $T$ 次拉杆后累积的懊悔总量，对于一次完整的 $T$ 步决策 $\left\{a_{1}, a_{2}, \ldots, a_{T}\right\}$ ，累积懊悔为 $\sigma_{R}=\mathbb{E}_{a\sim \pi}[\sum_{t=1}^{T} R\left(a_{t}^i\right)]$ 。MAB 问题的目标为最大化累积奖励，等价于最小化累积懊悔，即 $\text{min } \sigma_R=\text{max } \mathbb{E}_{a\sim \pi}[\sum_{t=1}^TQ(a_t^i)]$ 随着时间推移，total regret需要越来越小，那么探索一直都是必须的吗？

如果一直探索新策略： $KaTeX parse error: Undefined control sequence: \proptoT at position 9: \sigma_R\̲p̲r̲o̲p̲t̲o̲T̲\cdot R$ ， tota regret将线性递增，无法收敛；
如果一直不探索新策略： $\sigma_R\propto T\cdot R$ , total regret将线性递增。

是否存在一个方法具有次线性（sublinear）收敛保证的regret？

估计期望奖励

为了知道拉动哪一根拉杆能获得更高的奖励，我们需要估计拉动这根拉杆的期望奖励。由于只拉动一次拉杆获得的奖励存在随机性，所以需要多次拉动一根拉杆，然后计算得到的多次奖励的期望，其算法流程如下所示。

对于 $\forall a \in \mathcal{A}$ , 初始化计数器 $N (a) = 0$ 和期望奖励估值 $\hat{Q}(a)=0$
for $\rightarrow T$ do
- 选取某根拉杆，该动作记为 $a_{t}$
- 得到奖励 $r_{t}$
- 更新计数器: $N\left(a_{t}\right)=N\left(a_{t}\right)+1$
- 更新期望奖励估值: $\hat{Q}\left(a_{t}\right)=\hat{Q}\left(a_{t}\right)+\frac{1}{N\left(a_{t}\right)}\left[r_{t}-\hat{Q}\left(a_{t}\right)\right]$
end for

以上 for 循环中的第四步如此更新估值，是因为这样可以进行增量式的期望更新，公式如下：
$Q_k=\frac{1}{k}\sum_{i=1}^kr_i=\frac{1}{k}(r_k+\sum_{i=1}^{k−1}r_i)=\frac{1}{k}(r_k+(k−1)Q_{k−1})=\frac{1}{k}(r_k+kQ_{k−1}−Q_{k−1})=Q_{k−1}+\frac{1}{k}[r_k−Q_{k−1}]$

如果将所有数求和再除以次数，其缺点是每次更新的时间复杂度和空间复杂度均为 $O (n)$ 。而采用增量式更新，时间复杂度和空间复杂度均为 $O (1)$ 。

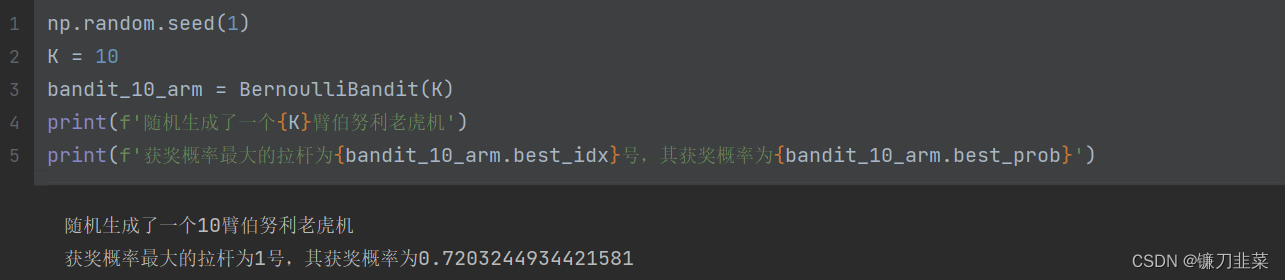
下面我们编写代码来实现一个拉杆数为 10 的多臂老虎机。其中拉动每根拉杆的奖励服从伯努利分布 (Bernoulli distribution)，即每次拉下拉杆有 $p$ 的概率获得的奖励为 $1$ . 有 $1 - p$ 的概率获得的奖励为 $0$ 。奖励为 $1$ 代表获奖, 奖励为 $0$ 代表没有获奖。

import numpy as np
import matplotlib.pyplot as plt

class BernoulliBandit:
    """伯努利多臂老虎机，输入k表示拉杆个数"""
    def __init__(self, K):
        self.probs = np.random.uniform(size=K) # 随机生成k个0~1的数，作为拉动每根拉杆的奖励
        # 概率
        self.best_idx = np.argmax(self.probs) # 奖励概率最大的拉杆
        self.best_prob = self.probs[self.best_idx] # 最大的奖励概率值
        self.K = K
    def step(self, k):
        # 当玩家选择了k号拉杆后，根据拉动该老虎机的k号拉杆获得奖励的概率返回1(获奖)或0(未获奖)
        if np.random.rand() < self.probs[k]:
            return 1
        else:
            return 0

执行结果
接下来我们用一个 Solver基础类来实现上述的多臂老虎机的求解方案。根据前文的算法流程，需要实现下列函数功能：根据策略选择动作、根据动作获取奖励、更新期望奖励估值、更新累积懊悔和计数。在下面的MAB算法基本框架中，我们将根据策略选择动作、根据动作获取奖励和更新期望奖励估值放在run_one_step()函数中，由每个继承Solver类的策略具体实现。而更新累积懊悔和计数则直接放在主循环run()中。

class Solver:
    """ 多臂老虎机算法基本框架 """

    def __init__(self, bandit):
        self.bandit = bandit
        self.counts = np.zeros(self.bandit.K)  # 每根拉杆的尝试次数
        self.regret = 0.  # 当前步的累积懊悔
        self.actions = []  # 维护一个列表,记录每一步的动作
        self.regrets = []  # 维护一个列表,记录每一步的累积懊悔

    def update_regret(self, k):
        # 计算累积懊悔并保存,k为本次动作选择的拉杆的编号
        self.regret += self.bandit.best_prob - self.bandit.probs[k]
        self.regrets.append(self.regret)

    def run_one_step(self):
        # 返回当前动作选择哪一根拉杆,由每个具体的策略实现
        raise NotImplementedError

    def run(self, num_steps):
        # 运行一定次数,num_steps为总运行次数
        for _ in range(num_steps):
            k = self.run_one_step()
            self.counts[k] += 1
            self.actions.append(k)
            self.update_regret(k)

贪心策略与 $\epsilon$ -greedy策略

完全贪心算法即在每一时刻采取期望奖励估值最大的动作，这就是纯粹的利用，而没有探索。所以通常要对完全贪心算法进行一些修改，比较经典的方法是 $\epsilon$ -greedy策略。 $\epsilon$ -greedy算法是在完全贪心算法的基础上增加了噪声，每次以概率1- $\epsilon$ 选择遗忘经验中期望奖励估值最大的那根拉杆（利用），以概率 $\epsilon$ 随机选择一根拉杆（探索）。贪心策略与 $\epsilon$ 贪心策略对比如下：
贪心策略比较
在 $\epsilon$ -greedy策略的具体实现中，令 $\epsilon$ 随时间衰减，即探索的概率将会不断降低。但是 $\epsilon$ 不会在有限的步数内衰减到0，因为基于有限步数观测的完全贪心算法仍然是一个局部信息的贪心算法，永远距离最优解有一个固定的差距。
衰减贪心策略
这样的缺点是很难找到合适的衰减规划。

不同 $\epsilon$ -greedy策略对比：Total Regret

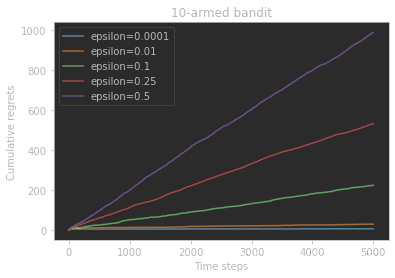
上图表明，基本上无论 $\epsilon$ 取值多少，累积懊悔都是线性增长的。随着 $\epsilon$ 的增大，累积懊悔增长的速率也会增大。

接下来尝试 $\epsilon$ 的值随时间衰减的 $\epsilon$ 贪心算法，采取的具体衰减形式为反比例衰减，公式为 $\epsilon_t=\frac{1}{t}$ 。

class DecayingEpsilonGreedy(Solver):
    """epsilon值随时间衰减的epsilon贪心算法，继承Solver类"""

    def __init__(self, bandit, init_prob=1.0):
        super(DecayingEpsilonGreedy, self).__init__(bandit)
        self.estimates = np.array([init_prob] * self.bandit.K)
        self.total_count = 0

    def run_one_step(self):
        self.total_count += 1
        if np.random.random() < 1 / self.total_count:  # epsilon值随时间衰减
            k = np.random.randint(0, self.bandit.K)
        else:
            k = np.argmax(self.estimates)

        r = self.bandit.step(k)
        self.estimates[k] += 1. / (self.counts[k] + 1) * (r - self.estimates[k])
        return k

np.random.seed(1)
decaying_epsilon_greedy_solver = DecayingEpsilonGreedy(bandit_10_arm)
decaying_epsilon_greedy_solver.run(5000)
print('epsilon值衰减的贪婪算法的累积懊悔为：',decaying_epsilon_greedy_solver.regret)
plot_results([decaying_epsilon_greedy_solver],["DecayingEpsilonGreedy"])

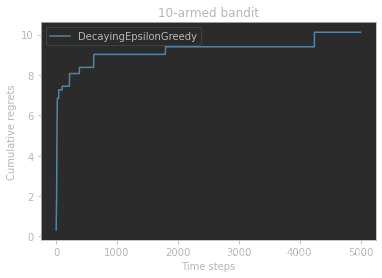
decaying
从图中可以看出，随着时间做反比衰减的 $\epsilon$ 贪心算法能够使累积懊悔与时间步的关系变成次线性（sublinear）的，这明显优于固定 $\epsilon$ 值的 $\epsilon$ 贪心算法。

上置信界算法

一根拉杆的不确定性越大，它就越具有探索的价值，因为探索之后可能发现它的期望奖励很大。引入不确定性度量 $U (a)$ ，它会随着一个动作被尝试次数的增加而减小。可以使用一种基于不确定性的策略来综合考虑现有的期望奖励估值和不确定性，其核心问题是如何估计不确定性。

上置信界（upper confidence bound, UCB）算法是一种经典的基于不确定性的策略算法，它的思想用到了一个非常著名的数学原理：霍夫丁不等式（Hoeffding’s inequality）。在霍夫丁不等式中，令 $X_1,...,X_n$ 为n个独立同分布的随机变量，取值范围为[0,1]，其经验期望为 $\bar{x}_n=\frac{1}{n}\sum_{j=1}^*X_j$ ，则有: $P(E[X]\ge \bar{x}_n+u)\le e^{-2nu^2}$

在概率论中，霍夫丁不等式给出了随机变量的和与其期望值偏差的概率上限，该不等式被Wassily Hoeffding于1963年提出并证明。霍夫丁不等式是Azuma-Hoeffding不等式的特例，它比Sergei Bernstein于1923年证明的Bernstein不等式更具一般性。这几个不等式都是McDiarmid不等式的特例。

将 $\hat{Q}(a_t)$ 代入 $\bar{x}_t$ ，不等式中的参数 $u=\hat{U}(a_t)$ 代表不确定性度量。给定一个概率 $p=e^{-2N(a_t)U(a_t)^2}$ ，根据上述不等式， $Q(a_t)<\hat{Q}(a_t)+\hat{U}(a_t)$ 至少以概率1-p成立。当p很小时， $Q(a_t)<\hat{Q}(a_t)+\hat{U}(a_t)$ 就以很大概率成立， $\hat{Q}(a_t)+\hat{U}(a_t)$ 便是期望奖励上届。此时上置信界算法便选取期望奖励上届最大的动作，即 $\max_{a\in A}[\hat{Q}(a)+\hat{U}(a)]$ 。那其中 $\hat{U}(a)$ 具体是什么呢？根据等式 $p=e^{-2N(a_t)U(a_t)^2}$ ，解之即得 $\hat{U}(a_t)=\sqrt{\frac{-log p}{2N(a_t)}}$ 。因此，设定一个概率p后，就可以计算相应的不确定性度量 $\hat{U(a_t)}$ 了。

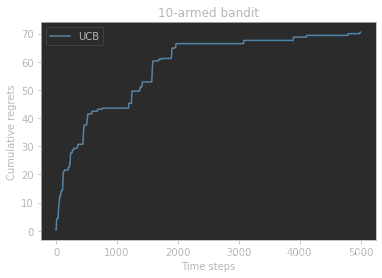
UCB 算法在每次选择拉杆前，先估计每根拉杆的期望奖励的上界，使得拉动每根拉杆的期望奖励只有一个较小的概率超过这个上界，接着选出期望奖励上界最大的拉杆，从而选择最有可能获得最大期望奖励的拉杆。

编写代码来实现UCB算法，在具体实现的过程中，设置 $p=\frac{1}{t}$ ，并且在分母中为拉动每根拉杆的次数加上常数1，以免出现分母为0的情形，即此时 $\hat{U}(a_t)=\sqrt{\frac{\log t}{2(N(a_t)+1)}}$ 。同时设定一个系数 $c$ 来控制不确定性比重，此时 $a_t=arg\max_{a\in A}[\hat{Q}(a)]$ 。

class UCB(Solver):
    """ UCB算法,继承Solver类 """

    def __init__(self, bandit, coef, init_prob=1.0):
        super(UCB, self).__init__(bandit)
        self.total_count = 0
        self.estimates = np.array([init_prob] * self.bandit.K)
        self.coef = coef

    def run_one_step(self):
        self.total_count += 1
        ucb = self.estimates + self.coef * np.sqrt(
            np.log(self.total_count) / (2 * (self.counts + 1)))  # 计算上置信界
        k = np.argmax(ucb)  # 选出上置信界最大的拉杆
        r = self.bandit.step(k)
        self.estimates[k] += 1. / (self.counts[k] + 1) * (r - self.estimates[k])
        return k


np.random.seed(1)
coef = 1  # 控制不确定性比重的系数
UCB_solver = UCB(bandit_10_arm, coef)
UCB_solver.run(5000)
print('上置信界算法的累积懊悔为：', UCB_solver.regret)
plot_results([UCB_solver], ["UCB"])

UCB

汤普森采样算法

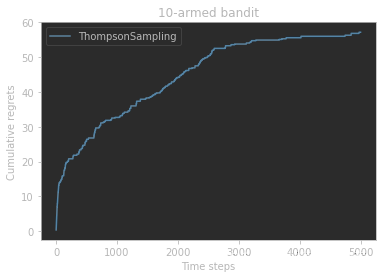
MAB中还有一种经典算法——汤普森采样（Thompson sampling），先假设拉动每根拉杆的奖励服从一个特定的概率分布，然后根据拉动每根拉杆的期望奖励来进行选择。但是由于计算所有拉杆的期望奖励的代价比较高，汤普森采样算法使用采样的方式，即根据当前每个动作 $a$ 的奖励概率分布进行一轮采样，得到一组各根拉杆的奖励样本，再选择样本中奖励最大的动作。

汤普森采样是一种计算所有拉杆的最高奖励概率的蒙特卡洛采样方法。

实际情况中，通常用Beta分布对当前每个动作的奖励概率分布进行建模。具体来说，如果某拉杆被选择了k次，其中 $m_1$ 次奖励为1， $m_2$ 次奖励为0，则该拉杆的奖励服从参数为 $m_1+1, m_2+1)$ 的Beta分布。

Beta分布是一种连续型概率密度分布，表示为 $x\sim Beta(a, b)$ ，由两个参数a, b决定，称为形状参数。由于其定义域为(0,1)，一般被用于建模伯努利试验事件成功的概率的概率分布。简单来说，beta分布可以看作一个概率的概率密度分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。

class ThompsonSampling(Solver):
    """汤普森采样算法，继承Solver类"""
    def __init__(self, bandit):
        super(ThompsonSampling, self).__init__(bandit)
        self._a = np.ones(self.bandit.K)  # 列表，表示每根拉杆奖励为1的次数
        self._b = np.ones(self.bandit.K)  # 列表，表示每根拉杆奖励为0的次数

    def run_one_step(self):
        samples = np.random.beta(self._a, self._b)  # 按照Beta分布采样一组奖励样本
        k = np.argmax(samples)  # 选出采样奖励最大的拉杆
        r = self.bandit.step(k)

        self._a[k]  += r  # 更新Beta分布的第一个参数
        self._b[k] += (1-r)  # 更新Beta分布的第二个参数
        return k

np.random.seed(1)
thompson_sampling_solver = ThompsonSampling(bandit_10_arm)
thompson_sampling_solver.run(5000)
print('汤普森采样算法的累积懊悔为：',thompson_sampling_solver.regret)
plot_results([thompson_sampling_solver], ["ThompsonSampling"])