开关电源——DCDC变换器设计
对于DCDC变换器来说,最重要的部分也是唯一一个磁学元件——电感需要考虑。
直流传递函数
正如之前我们所说,电感电流在开关导通的时候增加的电流必须等于在开关关断时候的减少的电流,即在一个工作周期中不积累能量,这称为 伏秒法则 。
V O N × t O N = V O F F × t O F F V_{ON} \times t_{ON} = V_{OFF} \times t_{OFF} VON×tON=VOFF×tOFF
则占空比表示为:
D = V O F F V O F F + V O N D = \frac{V_{OFF}}{V_{OFF} + V_{ON}} D=VOFF+VONVOFF
上式对于任意拓扑都适用,但是三种拓扑的传递函数不同本质是是因为他们的 V O N V_{ON} VON 和 V O F F V_{OFF} VOFF 的表达式不同。
下标给出了三种拓扑的推导函数:
| 拓扑 | V O N V_{ON} VON | V O F F V_{OFF} VOFF | DC传递函数 |
|---|---|---|---|
| Buck | V I N − V O V_{IN} - V_{O} VIN−VO | V O V_O VO | D = V O V I N D = \frac{V_{O}}{V_{IN}} D=VINVO |
| Boost | V I N V_{IN} VIN | V O − V I N V_O - V_{IN} VO−VIN | D = V O − V I N V O D = \frac{V_O - V_{IN}}{V_O} D=VOVO−VIN |
| Buck-Boost | V I N V_{IN} VIN | V O V_O VO | D = V O V I N + V O D = \frac{V_{O}}{V_{IN} + V_{O}} D=VIN+VOVO |
电感电流波形的直流分量和交流纹波
电感电流中存在两种分量:
I = I D C + Δ I I = I_{DC} + \Delta I I=IDC+ΔI
由 V = L d I d t V = L \frac{dI}{dt} V=LdtdI 可得:
Δ I = V Δ t / L \Delta I = V \Delta t / L ΔI=VΔt/L
因此电感电流的 纹波值 Δ I \Delta I ΔI 仅仅取决于伏秒数和电感量。
结论是,对于同一个电感,讨论它的伏秒数和讨论它的 Δ I \Delta I ΔI 其实是等效的。
伏秒数取决于输入和输出电压、频率和占空比。因此只有通过改变 L L L V V V f f f 或是 D D D 才能改变 Δ I \Delta I ΔI 。可见,如果仅改变负载电流不能改变 Δ I \Delta I ΔI 。
除了交流纹波之外,电感电流波形中还存在直流分量——即平均电流 I D C I_{DC} IDC 。他定义为纹波电流对称轴处的电流值,即 Δ I / 2 \Delta I / 2 ΔI/2 在它的上面,下面也有 Δ I / 2 \Delta I / 2 ΔI/2 。
需要指出的是 I D C I_{DC} IDC 仅决定传输能力——即维持相应输入输出功率的所需要的平均能量。这样,若变换器的工作条件——即输入输出电压和功率不变,就不能改变 I D C I_{DC} IDC 。因此,在一般的DCDC设计中, I D C I_{DC} IDC 一般是不易受到影响的。
现在我们来讨论 I D C I_{DC} IDC 和 I O I_O IO 之间的关系:
I D C = I O , for Buck I_{DC} = I_O, \text{for Buck} IDC=IO,for Buck
I D C = I O 1 − D , for Boost and Buck-Boost I_{DC} = \frac{I_O}{1 - D}, \text{for Boost and Buck-Boost} IDC=1−DIO,for Boost and Buck-Boost
结论是,对于Buck电路来说,仅改变 D D D 不会改变 I D C I_{DC} IDC 改变 I O I_O IO 才能改变 I D C I_{DC} IDC 。对于 Boost 和 Buck-Boost 来说,仅改变 D D D 就可以改变 I D C I_{DC} IDC 。
值得注意的是,对于 Boost 和 Buck-Boost 来说, I D C I_{DC} IDC 一定大于 I O I_O IO ,若占空比接近于1的时候,滤波电感的电流就会急剧增加。
交流电流、直流电流和峰值电流的确定
我们定义交流电流为:
I A C = Δ I 2 I_{AC} = \frac{\Delta I}{2} IAC=2ΔI
定义直流电流:
I L = I D C I_L = I_{DC} IL=IDC
线圈中的热损耗 P = I 2 R P = I^2R P=I2R 仅取决于直流电流,而磁损耗仅仅受交流电流 Δ I \Delta I ΔI 决定,与直流无关。
峰值电流是电感电流中最重要的电流量,因为它决定了电路中各种元件的最大电流上限。我们还知道,线圈中的磁场强度和瞬时电流成比例,若磁场强度超过了安全值,电感就会饱和(电感量开始下降)。一旦饱和,电感的限流能力随之下降,会有很大的电流通过开关管。所以,电感饱和是致命的,这总是发生在峰值电流的时刻,峰值电流定义为:
I P K = I D C + I A C I_{PK} = I_{DC} + I_{AC} IPK=IDC+IAC
易知:
2 I A C = Δ I = V Δ t L 2I_{AC} = \Delta I = \frac{V \Delta t}{L} 2IAC=ΔI=LVΔt
所以,电流纹波 I P P = Δ I I_{PP} = \Delta I IPP=ΔI 可直观的看做是电位电感上的伏秒数。
最“恶劣”输入电压的确定
到目前的分析中,我们总是假定固定输入电压,但是实际情况是输入电压有一个范围,即在最低输入电压 V I N M I N V_{INMIN} VINMIN 到 V I N M A X V_{INMAX} VINMAX 中。根据上一节的观点,瞬时峰值电流是很重要的,问题是何时产生峰值电流。所以,我们定义最大峰值电流对应的输入电压称为最“恶劣”输入电压。
要切记,无论哪种拓扑,当输入电压减小的时候,根据负反馈系统,占空比就要提升,因此大的占空比总是对应着低的输入电压。
- 对于Buck电路:
当输入电压增加的时候,占空比降低。但下降斜率 Δ I / t O F F \Delta I /t_{OFF} ΔI/tOFF 是不变的,因为其等于 V O / L V_O / L VO/L ,我们总是希望 V O V_O VO 不变,但是占空比降低 t O F F t_{OFF} tOFF 是增大的,因此只能 Δ I \Delta I ΔI 也增大。
同时,电感的平均电流 I L I_L IL 不变,因为其等于负载电流 I O I_O IO 。
因此,结论是: 对于Buck电路,最坏情况对应于最大输入电压 。
- 对于 Buck-Boost 电路:
当输入电压增大的时候,与Buck的情况相同,因为其 V O F F = V O V_{OFF} = V_O VOFF=VO 。交流电压增大。
现在分析直流分量,我们知道 I O = I L × ( 1 − D ) I_O = I_L \times (1 - D) IO=IL×(1−D) 。因此占空比减小, I L I_L IL 减小。
但是瞬时电流是交流与直流分量之和,大部分情况,交流分量的影响小于直流分量,所以当输入电压增大的时候,其实瞬时电流是降低的。
因此,结论是: 对于Buck-Boost电路,最坏情况对应于最小输入电压 。
- 对于 Boost 电路:
Boost电路的分析过程比较复杂,其下降斜率 Δ I / t O F F \Delta I /t_{OFF} ΔI/tOFF 是减小的,通过数学推导我们能够得出,当 D < 0.5 D < 0.5 D<0.5 的时候, Δ I \Delta I ΔI 随 D D D 的增加而增加,反之减小。
同样交流分量的影响小于直流分量,所以当输入电压增大的时候,其实瞬时电流是降低的。
因此,结论是: 对于Boost电路,最坏情况对应于最小输入电压 。
电流纹波率 r r r
现在我们引入DCDC变换器设计中最重要的参数,电流纹波率 r r r,其被定义为:
r = Δ I I L = 2 × I A C I D C r = \frac{\Delta I}{I_L} = 2 \times \frac{I_{AC}}{I_{DC}} r=ILΔI=2×IDCIAC
电流纹波率将两个看似不相关的变量 Δ I \Delta I ΔI 和 I L I_L IL 联系起来,因此设计者一旦确定了 r r r ,几乎所有的参数都能确定了。 r r r 的选择影响器件的选择和变换器的成本,应当清楚的认识这一点。
注意, r r r 的值是在连续导通CCM模式下定义的,因此有效范围在0-2之间。当 r = 0 r = 0 r=0 的时候,电流纹波为0,当 r = 2 r = 2 r=2 的时候,变换器处于临界导通模式BCM。
r r r 与电感量之间的关系
电流纹波率的表达式为:
r = Δ I I L = E t L μ H I L r = \frac{\Delta I}{I_L} = \frac{Et}{L_{\mu H}I_L} r=ILΔI=LμHILEt
其中 E t Et Et 定义为伏微秒数,而 L μ H L_{\mu H} LμH 是电感以 μ H \mu H μH 为单位的值。
下面给出一组常用公式:
r = E t L × I L = V O N × D L × I L × f = V O F F × ( 1 − D ) L × I L × f r = \frac{Et}{L \times I_L} = \frac{V_{ON} \times D}{L \times I_L \times f} = \frac{V_{OFF} \times (1 - D)}{L \times I_L \times f} r=L×ILEt=L×IL×fVON×D=L×IL×fVOFF×(1−D)
注意,上面的方程仅对于CCM模式有效。
因此, L L L 可以表示为:
L = V O N × D r × I L × f L = \frac{V_{ON} \times D}{r \times I_L \times f} L=r×IL×fVON×D
我们可以记为 L × I L L \times I_L L×IL 法则:
L × I L = E t r L \times I_L = \frac{Et}{r} L×IL=rEt
结论是,当确定了 r r r 也就基本确定了 L L L 的值。
r r r 的最佳值
研究表明, r r r 选择 0.4 是最合适的。
一般认为,电感的体积与电感的能量处理能力成正比,处理更高的能量需要性能更佳的电感,这通常对应着大磁芯。电感的能量处理能量最少要等于其希望储存的最大能量即 E = 1 2 × L × I P K 2 E = \frac{1}{2} \times L \times I_{PK}^2 E=21×L×IPK2 。否则,电感就会饱和。
通过实验研究,我们得到 r r r 与 E E E 的关系曲线:
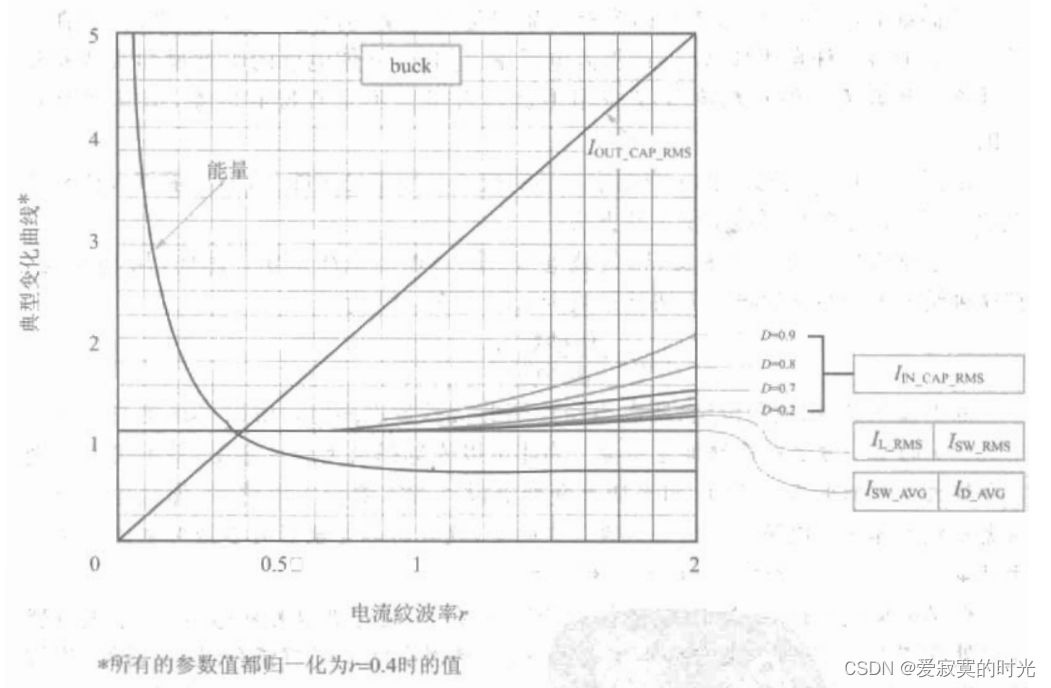
我们发现,在
r
=
0.4
r = 0.4
r=0.4 的时候有一处拐点,也就是说,当
r
r
r 比 0.4 小的时候,所需要的电感体积就会急速上升,当
r
r
r 大于 0.4 的时候,对于降低电感体积并没有太大效果。
同时,图中还给出了各种器件对于 r r r 的有效电流关系,我们发现,电容(特别是ESR比较大的电容)的有效电流值随着 r r r 的增大上升,大有效电流值对应着大的功耗,因此电容会发热严重,这是因为电容具有隔直作用功率不受直流分量的影响,而受纹波的影响。同时 r r r 对二极管、开关这类元件的影响很小,因为这类元件的功耗主要受直流分量的影响。
电感量和电感体积之间的关系
对于一个电感来说电感量和电感体积没有什么必要的关系,好像只需要将给定的磁芯上绕够一定的匝数即可,但其实是相关的。我们知道:
L × I L = E t r L \times I_L = \frac{Et}{r} L×IL=rEt
输入输出电压恒定,同时假设频率恒定,即伏秒数也恒定。同时 I L I_L IL 也是恒定的。也就是说 L L L 与 r r r 其实是成反比的,当 L L L 增大的时候, r r r 就会减小, r r r 的减小意味着需要更大体积的电感。
结论是,应用条件恒定的情况下,若 r r r 可变, L L L 与电感的体积成正相关。
当应用条件不恒定的情况,为了维持 r r r 在一个最佳值,例如增大负载电流,就需要增大电感的体积,增大能量处理能量,但是 L L L 的值需要减小,这是因为 r r r 不变。
频率对于电感量和电感体积的影响
若保持所有条件不变,仅仅使得 f f f 增加一倍,由于时间减少一半,则伏秒数也减小一半,因此 Δ I \Delta I ΔI 也减小一半,若 I D C I_{DC} IDC 不变,则 r r r 也减小一半。
若要使 r r r 维持不变,我们必须使得电感量也减小一半。
因此,结论是:
- 频率增加,所需电感体积减小(因为 r r r 不变, I D C I_{DC} IDC 不变,电流峰值不变,而 L L L减小,能量 E = 1 2 L I P K 2 E = \frac{1}{2} L I_{PK}^2 E=21LIPK2 减小)。
- 频率增加,所需电感量减小。
负载电流对电感量和电感体积的影响
若保持所有条件不变,仅将负载电流增大一倍,由于 Δ I \Delta I ΔI 没有变化, r r r 减少一半,为了使得 r r r 恢复为原来的最佳值,则需要使得 Δ I \Delta I ΔI 也增大一倍,伏秒数不变,我们只能使得电感量减小一半。
所以,结论是,负载电流与电感量成反比。
对于电感体积,我们知道 r r r 不变, Δ I \Delta I ΔI 和 I L I_L IL 同时增大一倍,则峰值电流增大一倍,但是电感量减少一半,可知 E E E 增大一倍。
所以,结论是,负载电流与电感体积成正比。
成品电感的参数和选型
成品电感的参数通常有:最大电流值( I D C I_{DC} IDC) ,最大有效电流值( I R M S I_{RMS} IRMS),饱和电流( I S A T I_{SAT} ISAT)。对于DCDC变换器而言,最大电流值等于最大有效电流值,而最后一个饱和电流是电感饱和之前的安全电流值。一般而言,我们只会考虑其中的最小值,因为任何应用也不会让电流超过其中之一。
但是必须牢记,大磁芯(高能量处理能力)通常会影响价格,多一些铜线(大电感量)对价格影响极小。