推导
DPM-Solver1的误差
由正文所述:
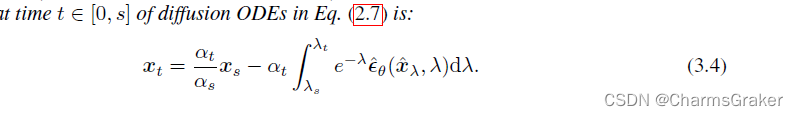
利用泰勒展开:
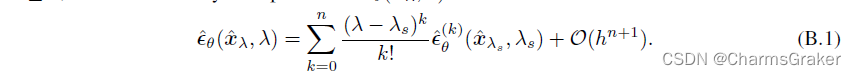
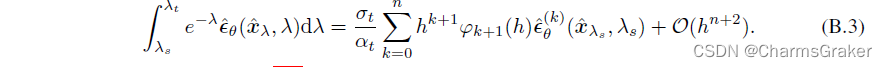
B.3式就是换了个元
δ
=
λ
−
λ
s
λ
t
−
λ
s
\delta=\frac{\lambda-\lambda_s}{\lambda_t-\lambda_s}
δ=λt−λsλ−λs,代入论文公式(3.4)的积分项(不含系数),这里先对B.4式简单代一下,注意到
h
=
λ
t
−
λ
s
h=\lambda_t- \lambda_s
h=λt−λs
∫
λ
s
λ
t
e
−
λ
ϵ
^
(
x
^
λ
s
,
λ
s
)
d
λ
=
∫
0
1
e
−
(
h
δ
+
λ
s
)
∑
k
=
0
n
δ
k
⋅
h
k
k
!
ϵ
^
(
k
)
(
x
^
λ
s
,
λ
s
)
h
(
d
δ
)
\int_{\lambda_s}^{\lambda_t}e^{-\lambda}\hat\epsilon(\hat x_{\lambda_s},\lambda_s)d\lambda= \int_{0}^{1}e^{-(h\delta + \lambda_s)}\sum_{k=0}^{n} \frac{\delta^k ·h^k}{k!} \hat \epsilon^{(k)}(\hat x_{\lambda_s},\lambda_s)h(d\delta)
∫λsλte−λϵ^(x^λs,λs)dλ=∫01e−(hδ+λs)k=0∑nk!δk⋅hkϵ^(k)(x^λs,λs)h(dδ)
=
∫
0
1
e
(
1
−
δ
)
h
−
(
h
+
λ
s
)
∑
k
=
0
n
δ
k
⋅
h
k
k
!
ϵ
^
(
k
)
(
x
^
λ
s
,
λ
s
)
h
(
d
δ
)
=
σ
t
α
t
∫
0
1
e
(
1
−
δ
)
h
∑
k
=
0
n
h
k
+
1
δ
k
k
!
ϵ
^
(
k
)
(
x
^
λ
s
,
λ
s
)
d
δ
=
σ
t
α
t
∑
k
=
0
n
h
k
+
1
∫
0
1
[
δ
k
k
!
ϵ
^
(
k
)
e
(
1
−
δ
)
h
]
ϵ
^
(
k
)
(
x
^
λ
s
,
λ
s
)
d
δ
=
σ
t
α
t
∑
k
=
0
n
h
k
+
1
φ
k
+
1
(
h
)
ϵ
^
(
k
)
(
x
^
λ
s
,
λ
s
)
d
δ
=\int_{0}^{1}e^{(1-\delta )h -(h+\lambda_s)}\sum_{k=0}^{n} \frac{\delta^k ·h^k}{k!} \hat \epsilon^{(k)}(\hat x_{\lambda_s},\lambda_s)h(d\delta)\\ =\frac{\sigma_t}{\alpha_t}\int_{0}^{1}e^{(1-\delta )h}\sum_{k=0}^{n} h^{k+1}\frac{\delta^k }{k!} \hat \epsilon^{(k)}(\hat x_{\lambda_s},\lambda_s)d\delta\\ =\frac{\sigma_t}{\alpha_t}\sum_{k=0}^{n} h^{k+1}\int_{0}^{1}[\frac{\delta^k }{k!} \hat \epsilon^{(k)}e^{(1-\delta )h}] \hat \epsilon^{(k)}(\hat x_{\lambda_s},\lambda_s)d\delta\\ =\frac{\sigma_t}{\alpha_t}\sum_{k=0}^{n} h^{k+1}\varphi_{k+1}(h) \hat \epsilon^{(k)}(\hat x_{\lambda_s},\lambda_s)d\delta
=∫01e(1−δ)h−(h+λs)k=0∑nk!δk⋅hkϵ^(k)(x^λs,λs)h(dδ)=αtσt∫01e(1−δ)hk=0∑nhk+1k!δkϵ^(k)(x^λs,λs)dδ=αtσtk=0∑nhk+1∫01[k!δkϵ^(k)e(1−δ)h]ϵ^(k)(x^λs,λs)dδ=αtσtk=0∑nhk+1φk+1(h)ϵ^(k)(x^λs,λs)dδ
其中
φ
k
(
z
)
\varphi_{k}(z)
φk(z)的定义如附录的B.2所示:
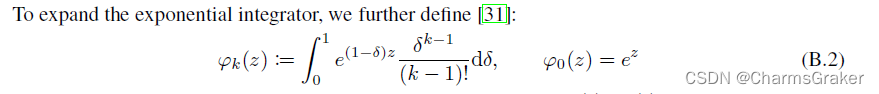
从而根据上面的推导,得到了B.4式
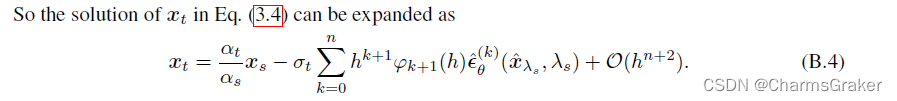
至于为什么要这样配凑,文中给出了参考文献。(之后再看看)
注意以下结论成立,在推导DPM-Solver2会用到
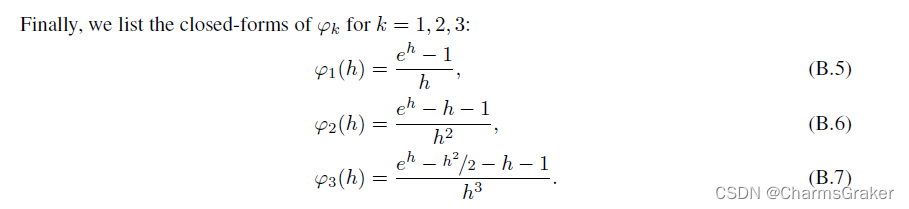
下面说明了k=1时候的误差,主要是利用已得到的B.4式验证3.7式的估计
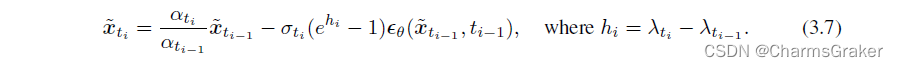
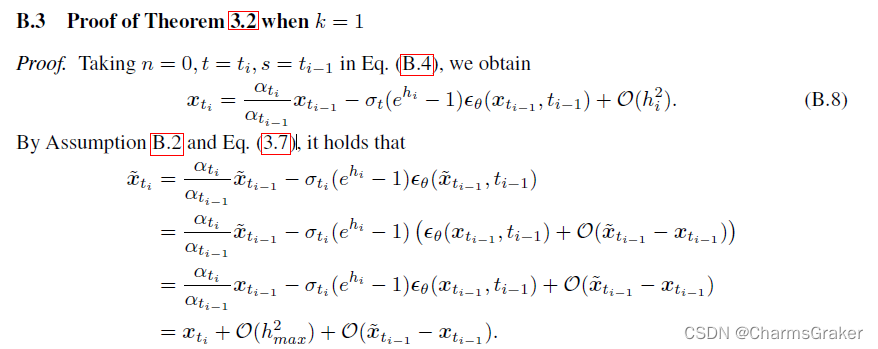
由最后一行将
x
t
i
x_{t_i}
xti移动一下,那么对右式不断重复即可。
DPM-Solver2的误差
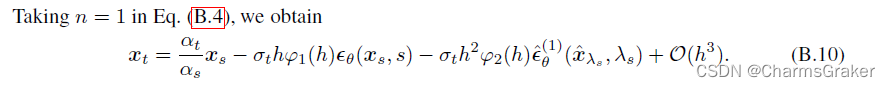
论文的叙述方式是假设算法4成立了,直接验证误差了。


如果考虑是如何构造出DPM-Solver2的,对于这个算法的个人理解是这样的。
首先DPM-Solver-1已经保证了是O(h),自然只需要考虑
x
^
t
\hat x_t
x^t的泰勒展开中的第n=1项,也就是一阶导数项,但这个导数不能求。于是得想个法子抹掉他还使得估计又不错。
注意到
h
2
φ
2
(
h
)
=
e
h
−
h
−
1
h^2 \varphi_2(h)=e^h - h - 1
h2φ2(h)=eh−h−1已经是
O
(
h
2
)
O(h^2)
O(h2)的了,那么实际上DPM-Solver-2只需要估计
x
^
t
−
x
t
\hat x_t-x_t
x^t−xt中含
h
2
ε
(
2
)
h^2 \varepsilon^{(2)}
h2ε(2)的项就可以了。
与此相仿,注意到
h
φ
1
(
h
)
=
e
h
−
1
h \varphi_1(h)=e^h-1
hφ1(h)=eh−1也已经是
O
(
h
)
O(h)
O(h)了,那就巧了,我能不能构造选取那个离
λ
s
\lambda_s
λs有
r
1
h
r_1h
r1h远的点来近似呢?于是可以用$
h
2
φ
(
h
)
h^2\varphi(h)
h2φ(h)来估计一下
φ
2
\varphi_2
φ2呢?自然是可以(因为假设了利普西茨条件),于是这里选取的就是
λ
s
1
−
λ
s
=
r
1
h
\lambda_{s_1}-\lambda_s=r_1h
λs1−λs=r1h,这样就行了,也不需要真的去计算这个一阶导数。
但上面的关键点就在于这个
φ
\varphi
φ函数的构造和利普西茨条件的有界