双钥加密体制
怎么说
没找着公钥加密在哪,所以就接着写了。
公钥加密,也叫非对称(密钥)加密,属于通信科技下的网络安全二级学科,指的是由对应的一对唯一性密钥(即公开密钥和私有密钥)组成的加密方法。它解决了密钥的发布和管理问题,是商业密码的核心。在公钥加密体制中,没有公开的是私钥,公开的是公钥。
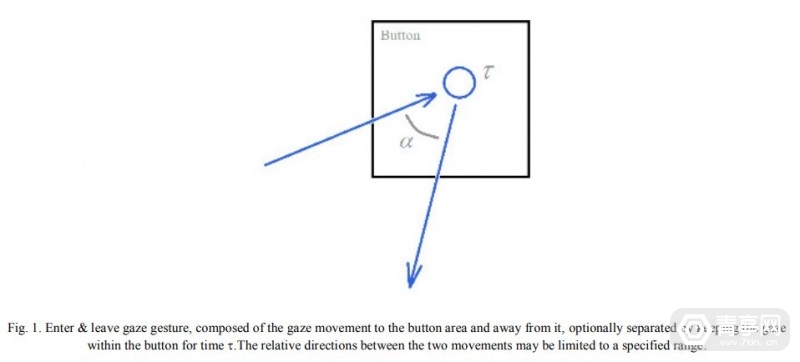
下面,三只和一只将为您展示公钥加密过程。如下图所示。
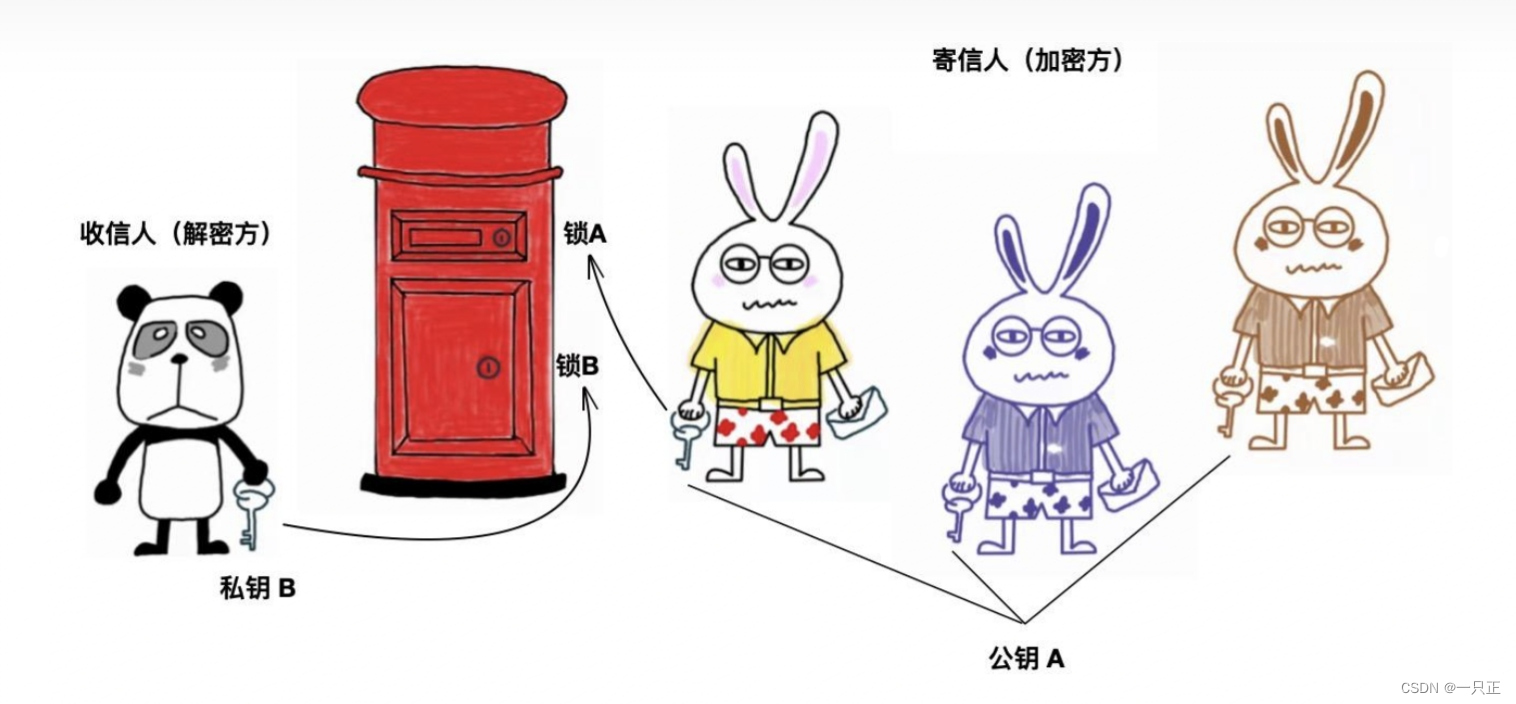
非对称加、解密过程:
消息接收方准备好公钥和私钥
私钥接收方自己留存、公钥发布给消息发送方
消息发送方使用接收方公钥对消息进行加密
消息接收方用自己的私钥对消息解密
欧几里得算法求逆
算数
例题,求17在模26下的逆元。
17x=1 mod 26
26=1×17+9,17=9+8,9=8×1+1
1=9-8=2×9-17=2×26-3×17..17-1 mod 26=-3=23 mod 26
算式
求x在mod x+x+x+x+1下的逆元
首先需要证明x2和
mod x+x+x+x+1的最大公约数
为1,否则不存在这个逆元。
28+x4+x+x+1=(2°+x+x)x+x+1x2=x(x+1)-x
x+1=(-1)(-x)+1
倒推下来:
1=(x+1)-x
-x=x2-x(x+1).1=(1-x)(1+x)+a2(1+x)=28+x4+x+x+1-(x°+x2+x)z2
..1=(1-x)[25+x+2+x+1-(x5+a2+x)2+a2
=(1-x)(x8+x4+x3+x+1)+(x7-25+x3-x+1)x2
..a在modax8+x+x+x+1下的逆元为(x7
-x5+x3-x+1)
RSA算法
加解密过程
选择一对不相等的大质数,记作p、q
计算N=p×q
计算(N)=(p-1)×(g-1)
选择一个与中(N)互质的整数e
计算出e对于中(N)的模反元素d
公钥KU=(e,N),私钥KR=(d,N)注意这括号不是最大公约数,而是表达形式,具体见例题!
如果两个正整数e和中(n)互质,那么一定可以找到一个整数d,使得ed-1被中(n)整除,或者说ed除以中(n)所得余数为1。此时,d就叫做e的模反元素。
加密Me modN=C
解密Cd modN=M
例题
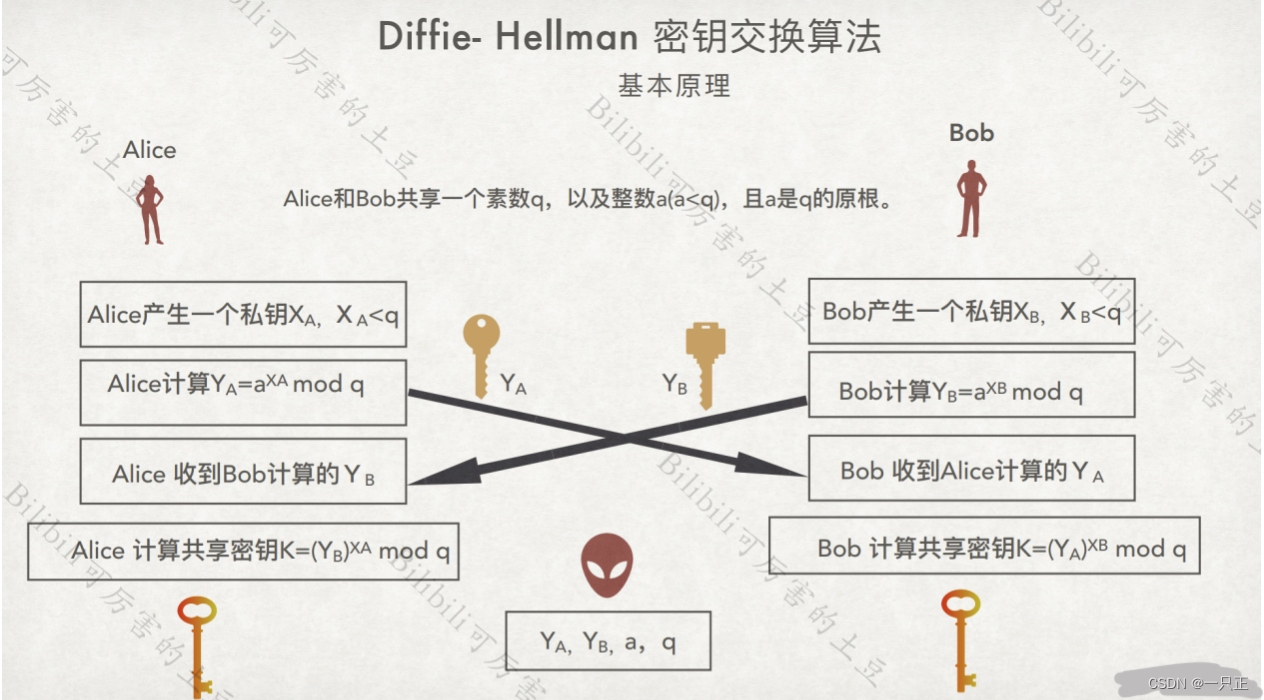
Diffie-Hellman 密钥交换算法
基本原理