概述

SM2是中国密码学算法标准中的一种非对称加密算法，它是由国家密码管理局（中国密码局）发布的一种椭圆曲线公钥密码算法。SM2基于椭圆曲线离散对数问题，主要用于数字签名、密钥交换和加密等密码学应用。

以下是SM2算法的主要特点和原理：

非对称加密：SM2使用非对称密钥加密体制，包括公钥和私钥。公钥用于加密数据和验证数字签名，私钥用于解密数据和生成数字签名。
椭圆曲线密码学：SM2基于椭圆曲线密码学，通过椭圆曲线上的点运算来实现加密和解密操作。SM2采用的是素数域上的椭圆曲线，具体是由国家密码管理局指定的一条256位的椭圆曲线。
安全性：SM2具有较高的安全性。它使用的椭圆曲线离散对数问题被认为是难以解决的数学难题，可以提供强大的安全性保障。同时，SM2还采用了一系列安全性增强措施，如密钥派生函数和随机数生成算法，以防止各种攻击。
数字签名：SM2可以用于生成和验证数字签名。发送方可以使用私钥对数据进行签名，接收方使用相应的公钥来验证签名的有效性。数字签名可以确保数据的完整性和身份认证，防止数据被篡改或冒充。
密钥交换：SM2还可以用于密钥交换，双方可以使用各自的私钥和对方的公钥来生成一个共享密钥，用于后续的对称加密通信。

SM2作为中国密码学标准的一部分，被广泛应用于各种信息安全领域，包括电子商务、移动支付、互联网金融等。它具有较高的安全性和性能表现，并得到了国际密码学界的认可和关注。

功能

密钥生成：
- 随机选择一个私钥（随机数），通常是一个256位的随机数。
- 使用椭圆曲线上的点运算，将私钥与基点（椭圆曲线上的固定点）相乘，得到公钥。公钥是一个曲线上的点，可以表示为(x, y)坐标。
加密：
- 随机选择一个临时私钥（临时随机数），通常是一个256位的随机数。
- 使用临时私钥与基点相乘，得到临时公钥。
- 将明文数据转换为椭圆曲线上的点（编码）。
- 生成一个随机数k，与临时公钥进行点运算，得到C1点。
- 使用接收方的公钥进行点运算，将C1点与明文数据进行异或运算，得到C2点。
- 使用临时私钥与C1点相乘，得到一个数值。
- 对C2点和该数值进行哈希运算，得到C3点。
- 将C1、C2和C3点组成密文。
解密：
- 使用私钥与C1点相乘，得到一个数值。
- 对C2点和该数值进行哈希运算，得到C3点。
- 将C1、C2和C3点组成密文。
- 使用接收方的私钥与C1点相乘，得到临时公钥。
- 使用临时公钥进行点运算，将C1点与C2点进行异或运算，得到明文数据。
数字签名：
- 对待签名数据进行哈希运算，得到哈希值。
- 随机选择一个数值k，与基点相乘，得到点（x1, y1）。
- 将x1的值与哈希值进行异或运算，得到一个数值。
- 计算该数值的模反函数，得到另一个数值。
- 将哈希值与另一个数值进行相乘，得到一个数值。
- 使用私钥与该数值相乘，得到一个数值。
- 使用点（x1, y1）与该数值进行点运算，得到点（x2, y2）。

将x2的值与哈希值进行比较，如果相等，则签名有效。

在SM2算法中，加密和解密是绑定在一起的，需要使用一对密钥，即公钥和私钥。发送方使用接收方的公钥进行加密，接收方使用自己的私钥进行解密。因此，加解密是作为一个整体功能进行使用的。

数字签名功能是可以独立使用的。发送方可以使用自己的私钥生成数字签名，并将签名附加在数据上发送给接收方。接收方使用发送方的公钥来验证数字签名的有效性，从而确保数据的完整性和身份认证。

密钥生成是SM2算法的前置步骤，它用于生成一对公钥和私钥。这对密钥可以用于后续的加解密和数字签名操作。因此，密钥生成是一个单独的功能，它为之后的加解密和数字签名提供了必要的密钥。

综上所述，可以将SM2的加解密作为一个绑定的功能，数字签名作为一个独立的功能，并单独考虑密钥生成作为另一个功能。

密钥生成

基点G的生成

基点G（也称为生成点、基点或基础点）是椭圆曲线上的一个特殊点，用于执行关键的操作和生成密钥对。

基点G的主要用途有两个：

密钥生成：基点G可以用作生成密钥对的基础。通过在椭圆曲线上对基点G进行重复的点运算，可以生成一系列相关的点，其中的某些点可用作公钥，另一些点可用作私钥。
密钥交换：基点G还可以用于执行密钥交换协议。参与者可以利用基点G和一些算法，通过交换计算的中间结果，最终协商出共享的密钥。

每个椭圆曲线都有一个对应的基点G（一对一的），这个基点是特定椭圆曲线上的一个固定点。基点G是椭圆曲线密码学中非常重要的组成部分，它定义了椭圆曲线上的加法运算和密钥生成过程。

通常，在设计椭圆曲线时，会选择一个合适的素数域模数p和相应的椭圆曲线方程。然后，根据特定的算法和安全要求，计算出一个合适的基点G，并确保它满足一些数学性质，如阶（order）和循环性。

一个模数p和一个椭圆曲线方程可以唯一确定一个基点G。

基点G是曲线上的一个特殊点，它需要满足一些附加条件才能成为合适的基点。这些条件包括：

在椭圆曲线上：基点G必须位于椭圆曲线上，即满足椭圆曲线方程。
有合适的阶（order）：基点G的阶是指它与自身的倍数相加的结果的个数。一个好的基点应该有一个适当大的阶，以提供足够的安全性。
循环性：基点G的倍数相加应该能够遍历曲线上的所有点，不会出现重复的点。这种循环性是基于基点G的阶。

假设我们有一个椭圆曲线方程为：

E: y^2 = x^3 + ax + b

其中，a和b是曲线的系数。

首先，需要选择一个合适的素数域的模数p，以及系数a和b的取值。
根据选择的模数p和系数a、b，计算出满足椭圆曲线方程的所有点的集合。
接下来，需要计算椭圆曲线的阶。阶是指基点G与自身的倍数相加所能生成的点的个数。
从曲线上选择一个点P作为候选的基点。
对于点P，进行倍点运算，即将点P与自身相加，得到2P、3P、4P，依此类推，直到计算得到一个循环的效果，即nP = O，其中O表示无穷远点（曲线上不存在的特殊点）。
如果得到的循环的长度等于阶，那么点P就可以作为基点G。

总结来说，通过椭圆曲线的方程，我们可以计算出满足方程的所有点的集合。然后，在这些点中选择一个候选的基点，并进行倍点运算，验证是否满足循环的条件。如果满足循环的条件，那么该点就可以作为椭圆曲线的基点G

模数p

模数p在椭圆曲线密码学中扮演着重要的角色，具有以下几个作用：

定义域限制：模数p确定了椭圆曲线方程中的坐标值的范围。椭圆曲线的点坐标通常是模p的剩余类（residue class），即在0到p-1之间的整数。这样，模数p限制了椭圆曲线上的点在哪个有限域上运算。
安全性：选择适当的模数p对椭圆曲线密码学的安全性至关重要。模数p的大小应根据安全要求来确定，通常应该是一个大素数。较大的模数可以增加椭圆曲线离散对数问题的计算复杂度，提供更高的安全性。
运算性能：模数p的大小也会影响椭圆曲线的计算性能。较小的模数可以加快计算速度，但可能会降低安全性。选择合适的模数需要在安全性和性能之间进行权衡。
数字表示和存储：模数p决定了椭圆曲线上的点在计算机系统中的表示和存储方式。通常，点坐标需要使用固定长度的二进制表示，模数p决定了这个长度。

密钥生成过程

SM2算法的密钥生成过程如下：

选择椭圆曲线参数：选择一个适当的椭圆曲线作为密码学基础，SM2标准中规定了一条256位的椭圆曲线。
生成私钥：随机选择一个私钥d，通常是一个256位的随机数。
计算公钥：使用椭圆曲线上的点运算，将基点G（椭圆曲线上的固定点）与私钥d相乘，得到公钥Q。具体计算公式为 Q = d * G。
公钥编码：将公钥Q的坐标（x, y）进行编码，常用的编码方式为压缩编码或非压缩编码。

示例：

假设我们选择了一条椭圆曲线，其参数为：

曲线方程：y^2 = x^3 + ax + b

椭圆曲线参数：a = 0，b = 7

基点G的坐标：(x_G, y_G)

选择私钥： 私钥d = 1234567890abcdef1234567890abcdef1234567890abcdef1234567890abcdef
计算公钥： 进行椭圆曲线上的点运算，将基点G与私钥d相乘。 Q = d * G
公钥编码： 将公钥Q的坐标（x_Q, y_Q）进行编码，得到最终的公钥。

例如，压缩编码方式下，公钥的编码形式为：公钥 = 02 || x_Q（其中02表示y坐标为偶数）。

这样，我们就完成了SM2算法的密钥生成过程。通过随机选择私钥，再经过椭圆曲线上的点运算，我们可以得到一对公钥和私钥，用于后续的加解密和数字签名操作。

对公钥进行编码是为了在实际应用中更方便地传输和存储公钥信息。

在椭圆曲线密码学中，公钥通常由椭圆曲线上的一个点表示，该点的坐标是一个有限域中的元素。公钥的坐标可以是(x, y)形式的非压缩表示，也可以是压缩表示，只包含其中一个坐标和一个标志位。

在SM2算法中，为了减少公钥的传输大小和存储空间，通常使用压缩编码或非压缩编码方式对公钥进行表示。压缩编码只包含一个坐标和一个标志位，而非压缩编码则包含两个坐标。

通过编码，公钥的表示形式变得更紧凑，占用的空间更小，有助于提高效率和降低资源消耗。在实际使用中，编码后的公钥可以更方便地传输、存储和处理。

需要注意的是，在使用公钥进行加密、数字签名验证等操作时，需要根据编码方式对公钥进行解码，以恢复到椭圆曲线上的点形式进行运算。

加解密

SM2算法的加解密过程如下：

加密过程：

现在我们有一个基点G，还有基点G的阶n（即nG=O,O为无穷远点）

选择一个随机数k，1<=k<=n-1

C1=kG,又因为kG肯定不为O，所以kG对应着椭圆曲线中的一个点，设为（x1,y1）

所以可以看作将（x1,y1）表示为比特串，这个比特串为C1

S的作用是作为数字签名，接收方可以自行再计算一个S来和收到的S进行对比，如果相同，就没问题

t其实就相当于加密密钥，算出来t与明文M异或就可以得到密文

因为基点G，发送方是不会发送给接收方的，但是没有G又无法解密，C1的作用是可以在不需要基点G的情况下进行解密（这地方我当时卡了十几分钟都没明白C1是干啥的）

在SM2算法中，加密后的密文C由三个部分组成：

C1：这是一个椭圆曲线上的点，表示加密过程中生成的临时公钥点Q'。这个点的坐标可以用压缩或非压缩编码表示。
C2：这是一个椭圆曲线上的点，表示加密后的数据。它与明文数据M进行异或运算后得到。C2 = M ⊕ (Q' * Pb)，其中Pb是接收方的公钥点。
C3：这是一个哈希值，用于验证密文的完整性。H是对C2点和临时私钥与C1点的运算结果进行哈希运算得到的。

解密过程：

（但是我按照书上的算法列出了两个S的计算方式，S的相同需要k和d_B数值相同，这一点我也没搞明白）

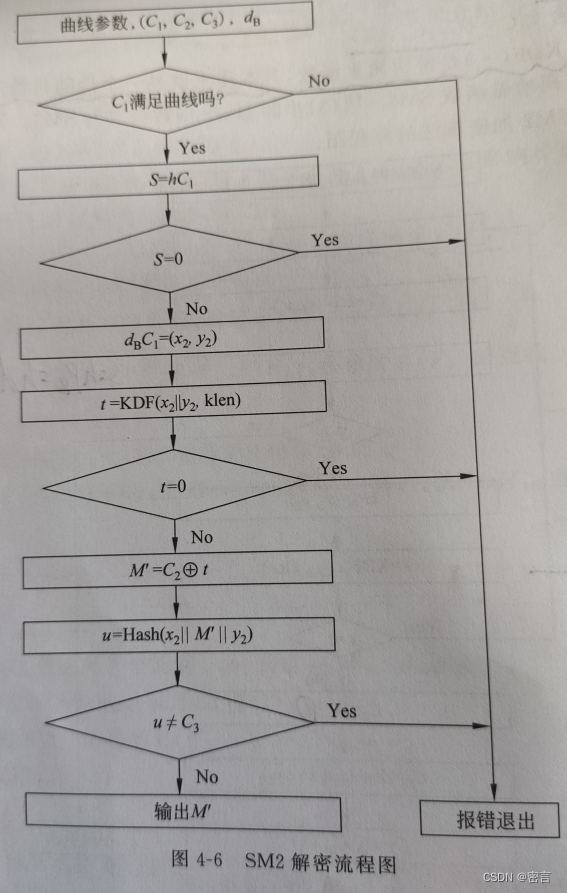
通过这个图应该可以看出C1的作用，可以避免传输G，又可以进行解密

数字签名

概述

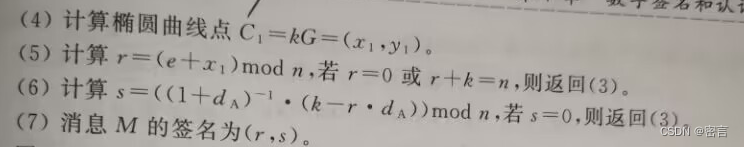
第4步目的还是在避免传输基点G的条件下帮助解码

对第5步r的计算方式分析

在SM2数字签名算法中，计算参数 r = (e + x) mod n 的目的是为了生成签名中的 r 值，其中 e 是哈希值 H 的整数表示，x 是临时公钥 K 的 x 坐标，n 是曲线的阶数。下面是每个参数的具体作用：

哈希值 H (e)：
- 哈希值 H 是对待签名的消息进行哈希运算后得到的结果。
- 它确保了消息的完整性和唯一性。
- 在签名过程中，将哈希值 H 用作计算参数 r 的一部分，确保签名与消息相关联。
临时公钥的 x 坐标 (x)：
- 在签名过程中，通过临时私钥 k 计算临时公钥 K = k * G。
- 临时公钥 K 的 x 坐标 x 被用作计算参数 r 的一部分。
- 这样可以确保签名的随机性和唯一性，因为每次使用不同的临时私钥 k，都会生成不同的临时公钥 K。
曲线的阶数 n：
- 曲线的阶数 n 表示椭圆曲线上点的数量。
- 在签名过程中，n 用作计算参数 r 的模数，即进行取模运算。
- 这确保了计算出的 r 值在一定范围内，并且与曲线的特性相对应。

综上所述，计算参数 r = (e + x) mod n 的过程中，哈希值 H、临时公钥的 x 坐标 x 和曲线的阶数 n 扮演着重要的角色：

哈希值 H 保证了签名与消息相关联，确保签名的唯一性。
临时公钥的 x 坐标 x 增加了签名的随机性和抗攻击性。
曲线的阶数 n 用于将计算结果限制在一定范围内，符合椭圆曲线的特性。

这些参数的选择和计算是为了增加签名的安全性、随机性和可验证性，使得SM2数字签名算法具备良好的性质和保护特性。

对第6步s的计算方式分析

在SM2数字签名算法中，计算参数 s 的目的是生成签名中的 s 值，其中 d 是私钥，k 是临时私钥，r 是签名参数。下面是每个参数的具体作用：

私钥 d：
- 私钥 d 是签名者拥有的私密信息，用于生成对应的公钥。
- 在计算参数 s 时，私钥 d 被用作计算的一部分。
临时私钥 k：
- 临时私钥 k 是在签名过程中生成的一个随机数。
- 它用于计算临时公钥 K = k * G 和生成签名中的 r 值。
签名参数 r：
- 签名参数 r 是在签名过程中计算得到的，与临时公钥的 x 坐标相关。
- 它用于验证签名的有效性。
曲线的阶数 n：
- 曲线的阶数 n 是椭圆曲线上点的数量，它也用作计算参数 s 的模数。

现在来解释计算参数 s = ((1 + d)^(-1) * (k - r * d)) mod n 的作用：

((1 + d)^(-1) * (k - r * d)) 表示一系列运算，包括私钥 d 和临时私钥 k 的运算。
(1 + d)^(-1) 是私钥 d 加一的逆元素，即 (1 + d) 的模逆，它的作用是确保计算参数 s 时的数学运算可逆。（"可逆" 这个特性是为了确保计算参数 s 的数学运算在验证过程中是可逆的，使得签名的验证能够得到正确的结果，并保证了签名的可靠性和可验证性。）
(k - r * d) 是临时私钥 k 减去 r 与私钥 d 乘积的结果，它的作用是确保计算参数 s 时包含了临时私钥 k 和签名参数 r 的信息。

最后，通过对计算结果进行取模运算 ((1 + d)^(-1) * (k - r * d)) mod n，保证了计算得到的参数 s 在一定范围内，并符合椭圆曲线的特性。

综上所述，计算参数 s 的过程中，私钥 d、临时私钥 k、签名参数 r 和曲线的阶数 n 扮演着重要的角色：

私钥 d 用于参与计算，确保签名的安全性和私密性。
临时私钥 k 和签名参数 r 用于计算 s，增加了签名的随机性和抗攻击性。
曲线的阶数 n 用于将计算结果限制在一定范围内，符合椭圆曲线的特性。

这些参数的选择和计算是为了增加签名的安全性、随机性和可验证性，使得SM2数字签名算法具备良好的性质和保护特性。

加密模式

在SM2算法中，有两种主要的加密模式用于加密数据，分别是C1C2C3模式（密文格式1）和C1C3C2模式（密文格式2）。

1. C1C2C3模式（密文格式1）：
- C1：随机生成的曲线上的点，用于混淆加密结果。它不直接包含加密数据，而是用于提供混淆和保护密文的安全性。
- C2：加密后的密文数据。这是对原始数据使用SM4对称加密算法进行加密得到的结果。
- C3：对加密数据的MAC值（消息认证码）。MAC用于验证数据的完整性和防止篡改。通过对加密数据进行消息认证，可以确保数据在传输过程中没有被篡改。

这种模式适用于对称加密的情况，其中使用SM4对称加密算法对数据进行加密。C1C2C3模式提供了数据机密性和完整性的保护。

2. C1C3C2模式（密文格式2）：
- C1：随机生成的曲线上的点，用于混淆加密结果。
- C3：对加密数据的MAC值（消息认证码）。与密文格式1相比，C3的位置发生了变化。
- C2：加密后的密文数据。这是使用SM2非对称加密算法对原始数据进行加密得到的结果。

这种模式适用于非对称加密的情况，其中使用SM2非对称加密算法对数据进行加密。C1C3C2模式也提供了数据机密性和完整性的保护，但与密文格式1相比，MAC值的位置发生了变化。

总的来说，这两种密文格式在加密过程中采用了不同的顺序和位置安排，但都保证了加密数据的机密性和完整性。具体选择哪种模式取决于应用场景和使用需求。

在C1C2C3模式中，先生成随机的曲线上的点C1，然后对原始数据使用SM4对称加密算法进行加密得到C2，最后计算加密数据的MAC值得到C3。

而在C1C3C2模式中，同样先生成随机的曲线上的点C1，然后对原始数据计算MAC值得到C3，最后再使用SM2非对称加密算法对原始数据进行加密得到C2。

两种模式对于C2、C3的计算的输入数据不同，一个是加密后的，一个是加密前的

优缺点

C1C2C3模式和C1C3C2模式在应用场景、优点和缺点方面有一些差异。以下是它们的一些特点：

C1C2C3模式（密文格式1）：
- 应用场景：适用于对称加密的情况，其中使用SM4对称加密算法对数据进行加密。
- 优点：
- 提供机密性：使用对称加密算法对数据进行加密，确保数据的保密性。
- 防篡改：通过计算MAC值，能够验证数据的完整性，防止数据在传输过程中被篡改。
- 缺点：
- 密文长度增加：由于需要包含C1、C2和C3，密文的长度相对较长。
- 仅适用于对称加密：该模式仅适用于对称加密算法，无法直接用于非对称加密算法。

C1C3C2模式（密文格式2）：
- 应用场景：适用于非对称加密的情况，其中使用SM2非对称加密算法对数据进行加密。
- 优点：
- 机密性和完整性：同样提供了机密性和完整性的保护，通过非对称加密算法和MAC值的计算。
- 简化解密过程：密文格式中C3位于C2之前，使得解密时先验证完整性，然后再进行解密操作。
- 缺点：
- 密文长度增加：与C1C2C3模式相同，密文长度相对较长。
- 仅适用于非对称加密：该模式仅适用于非对称加密算法，无法直接用于对称加密算法。

总体而言，选择使用哪种模式应基于具体的应用需求和标准规范。如果需要对称加密，可以选择C1C2C3模式；如果需要非对称加密，可以选择C1C3C2模式。同时，需要考虑密文长度和解密过程的复杂性。

论文和研究方向推荐

论文

"SM2密码算法在商用密码应用设计中的应用"，作者：王小云，刘军。该论文介绍了SM2算法的设计和实现，包括其密码学原理、密钥生成、加密和数字签名等内容。它提供了对该算法的全面理解。
"SM2密码系统的安全分析"，作者：赖学嘉，王小云，冯登国。该论文对SM2算法进行了安全性分析，包括对其密钥长度、抵抗各种攻击和潜在漏洞的评估。它提供了对SM2算法的密码学强度和安全性的洞察。
"SM2加密算法的高效安全椭圆曲线实现"，作者：龚光，乔克新。该论文侧重于SM2算法的高效实现，提供了在椭圆曲线上进行算术运算的优化技术。它讨论了实际实现的性能改进和安全性考虑。
"SM2数字签名算法的高效实现"，作者：杨波，刘树青，文伟强。该论文着重于SM2数字签名算法的高效实现，包括签名生成和验证的优化。它讨论了诸如基于窗口的标量乘法和预计算表等技术。
"SM2密码算法及其应用概述"，作者：曹志刚，陈克非，桂小林。该论文概述了SM2算法的特点、安全性和各种应用。它讨论了SM2在中国的应用以及其在国际标准化方面的潜力。