---

CSDN提示我字数太多，一篇发不下，只好拆分开

关于

• 标准DH模型
• 改进DH模型
• 机器人正运动学

的相关内容详见前一篇文章：

→→→【工业机器人运动学与Matlab正逆解算法学习笔记（用心总结一文全会）（一）】

❤ 2023.6.19 ❤

机器人逆运动学

※ 代数解、几何解，解析解（封闭解）、数值解的含义与联系

说起来我刚碰到这几个概念的时候还是挺晕的，和别人交流之后发现晕的不止我一个，经常有人把概念搞混、搞错。

下面有请ChatGPT先来回答一下

然后我总结一下

代数解和几何解都属于解析解（封闭解），他们的特点是可以列出具体的方程，求得的结果是精确的。不一样的地方是，代数解是根据矩阵的特性，通过特定元素相等的方法建立方程组，求解出未知数；而几何解是通过机器人的几何关系建立方程组，求解未知数。

只有特定构型的机器人存在解析解，不过好在我们平时用到的机器人大多数都是特定构型的。

数值解与解析解相对应，特点是运算过程靠迭代，求得的结果是近似解。他适用于所有机器人，包括特殊构型和一般构型，大多在不存在解析解的机器人上使用。

---

针对ZK-500机器人，因为属于后三轴交于一点的特殊构型，所以这里使用解析法求机器人逆解。

首先将位姿描述矩阵写成如下形式

$${}_6^{0}T=\left[\begin{array}{cccc}{n}_x& o_x& a_x& p_x\\ n_y& o_y& a_y& p_y\\ n_z& o_z& a_z& p_z\\ 0& 0& 0& 1\end{array}\right]={}_1^{0}T\left({\theta }_1\right){}_2^{1}T\left({\theta }_2\right){}_3^{2}T\left({\theta }_3\right){}_4^{3}T\left({\theta }_4\right){}_5^{4}T\left({\theta }_5\right){}_6^{5}T\left({\theta }_6\right)$$

○ 代数解求${\theta }_1$、${\theta }_2$、${\theta }_3$

※参考资料

→→→【MD-H模型运动学正解、逆解及姿态角的解算验证】
这真是个宝藏作者了

→→→《机器人学导论》（John J Craig）

---

· 求解${\theta }_1$

首先将上式中包含${\theta }_1$的部分移动到方程的左边

$${\left[{}_1^{0}T\left({\theta }_1\right)\right]}^{-1}{}_6^{0}T={}_2^{1}T\left({\theta }_2\right){}_3^{2}T\left({\theta }_3\right){}_4^{3}T\left({\theta }_4\right){}_5^{4}T\left({\theta }_5\right){}_6^{5}T\left({\theta }_6\right)$$

将${}_1^{0}T$求逆，等式写成如下形式

$$\left[\begin{array}{cccc}{c}_1& s_1& 0& 0\\ -s_1& c_1& 0& 0\\ 0& 0& 1& -d_1\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}{n}_x& o_x& a_x& p_x\\ n_y& o_y& a_y& p_y\\ n_z& o_z& a_z& p_z\\ 0& 0& 0& 1\end{array}\right]={}_6^{1}T$$

求解出${}_6^{1}T$后，通过观察等式两边的矩阵，令元素（2,4）相等得到

$$-s_1{p}_x+c_1{p}_y=0$$

---

• ※ 【这个方程是怎么得到的】

这个求解过程内容比较多，我姑且用matlab算了一下。。。

• 等式左边矩阵（每个方括号代表一行）

[nx*cos(Q1) + ny*sin(Q1), 
 ox*cos(Q1) + oy*sin(Q1), 
 ax*cos(Q1) + ay*sin(Q1), 
 px*cos(Q1) + py*sin(Q1)]
 
[ny*cos(Q1) - nx*sin(Q1), 
 oy*cos(Q1) - ox*sin(Q1), 
 ay*cos(Q1) - ax*sin(Q1), 
 py*cos(Q1) - px*sin(Q1)]
 
[nz,oz,az,pz - d1]

[0,0,0,1]

• 等式右边矩阵（每个方括号代表一行）

[- cos(Q6)*(sin(Q2 + Q3)*sin(Q5) - cos(Q2 + Q3)*cos(Q4)*cos(Q5)) - cos(Q2 + Q3)*sin(Q4)*sin(Q6),   
 sin(Q6)*(sin(Q2 + Q3)*sin(Q5) - cos(Q2 + Q3)*cos(Q4)*cos(Q5)) - cos(Q2 + Q3)*cos(Q6)*sin(Q4), 
 sin(Q2 + Q3)*cos(Q5) + cos(Q2 + Q3)*cos(Q4)*sin(Q5), 
 a1 + a3*cos(Q2 + Q3) + d4*sin(Q2 + Q3) + a2*cos(Q2)]
 
[- cos(Q4)*sin(Q6) - cos(Q5)*cos(Q6)*sin(Q4),
 cos(Q5)*sin(Q4)*sin(Q6) - cos(Q4)*cos(Q6),
 sin(Q4)*sin(Q5),
 0]
 
[cos(Q6)*(cos(Q2 + Q3)*sin(Q5) + sin(Q2 + Q3)*cos(Q4)*cos(Q5)) - sin(Q2 + Q3)*sin(Q4)*sin(Q6), 
 - sin(Q6)*(cos(Q2 + Q3)*sin(Q5) + sin(Q2 + Q3)*cos(Q4)*cos(Q5)) - sin(Q2 + Q3)*cos(Q6)*sin(Q4), 
 sin(Q2 + Q3)*cos(Q4)*sin(Q5) - cos(Q2 + Q3)*cos(Q5),      
 a3*sin(Q2 + Q3) - d4*cos(Q2 + Q3) + a2*sin(Q2)]
 
[0,0,0,1]
 

果然包含${\theta }_1$（这里是$Q_1$）的元素里面就（2,4）最好算。。。

---

式中，$p_x$、$p_y$均为已知，则${\theta }_1$可表示为：

$${\theta }_1=Atan2\left(p_y,p_x\right)$$

【！！】注意，这里用的是$Atan2\left(\right)$，这个函数与$\mathrm{Atan}\left(\right)$一样是求反正切，但是他的值域为$(-\pi ,\pi )$，可以得到角度对应的象限，是增强版的$\mathrm{Atan}\left(\right)$。还有需要注意的是输入变量先$p_y$再 $p_x$。
具体可以参考
→→→atan2()
→→→atan2 vs atan

此处存在两组解：
$${\theta }_1=Atan2\left(p_y,p_x\right)$$
或$${\theta }_1^{\prime }=Atan2\left(-p_y,-p_x\right)={\theta }_1+{180}^{\circ }$$

• matlab代码实现

%% theta1求解
%theta1可能的解有两组
theta1_1=atan2(py,px);
theta1_2=atan2(py,px)+pi;

---

· 求解${\theta }_3$

令上面等式中矩阵元素（1,4）和（3,4）左右相等得：

$$\begin{gathered} c_1{p}_x+s_1{p}_y=a_1+a_2{c}_2+a_3{c}_{23}+d_4{s}_{23} \\ {p}_z-d_1=a_2{s}_2+a_3{s}_{23}-d_4{c}_{23} \end{gathered}$$

等号左右平方和得
$$m^2+n^2=a_2^2+a_3^2+d_4^2+2a_2\left(a_3{c}_3+d_4{s}_3\right)$$
其中：
$$\begin{gathered} m=c_1{p}_x+s_1{p}_y-a_1 \\ n=p_z-d_1 \end{gathered}$$

---

关于这一步的计算过程：

我用这段代码演示：

syms a1 a2 a3 d4 theta2 theta3

m=a2*cos(theta2)+a3*cos(theta2+theta3)+d4*sin(theta2+theta3);
n=a2*sin(theta2)+a3*sin(theta2+theta3)-d4*cos(theta2+theta3);

k=m^2 + n^2

% 展开表达式为多项式形式
K1 = expand(m^2 + n^2) 
%K = collect(K, [a1 a2 a3 d4]);  

% 化简多项式
K2=simplify(K1)

% 整理多项式的项
k3=collect(K2)

结果：

k =
(a3*cos(theta2 + theta3) + d4*sin(theta2 + theta3) + a2*cos(theta2))^2 + (a3*sin(theta2 + theta3) - d4*cos(theta2 + theta3) + a2*sin(theta2))^2
 
K1 =
a2^2*cos(theta2)^2 + a2^2*sin(theta2)^2 + a3^2*cos(theta2)^2*cos(theta3)^2 + d4^2*cos(theta2)^2*cos(theta3)^2 + a3^2*cos(theta2)^2*sin(theta3)^2 + a3^2*cos(theta3)^2*sin(theta2)^2 + d4^2*cos(theta2)^2*sin(theta3)^2 + d4^2*cos(theta3)^2*sin(theta2)^2 + a3^2*sin(theta2)^2*sin(theta3)^2 + d4^2*sin(theta2)^2*sin(theta3)^2 + 2*a2*a3*cos(theta2)^2*cos(theta3) + 2*a2*a3*cos(theta3)*sin(theta2)^2 + 2*a2*d4*cos(theta2)^2*sin(theta3) + 2*a2*d4*sin(theta2)^2*sin(theta3)
 
K2 =
a2^2 + 2*cos(theta3)*a2*a3 + 2*sin(theta3)*a2*d4 + a3^2 + d4^2
 
k3 =
a2^2 + 2*cos(theta3)*a2*a3 + 2*sin(theta3)*a2*d4 + a3^2 + d4^2

---

令$H=\left(m^2+n^2-a_2^2-a_3^2-d_4^2\right)/2a_2$
则可将等式表示为：
$$a_3{c}_3+d_4{s}_3=H$$

可得：
$${\theta }_3=Atan2\left(H,\pm \sqrt{a_3^2+d_4^2-H^2}\right)-Atan2\left(a_3,d_4\right)$$

由于正负号的存在，${\theta }_3$存在两组解。

---

• ※ 【关于这一步是怎么来的】

我没有找到转换成反正切的具体的内容，但是这个推导过程可以参考

→→→【acosx+bsinx = c;计算x怎么求】

---

• matlab代码实现

%% theta3求解
%theta1的取值已经确定，但是因为theta1有两组可能得解，所以这里实际上m有两组取值，这里只给出一组
m=cos(theta1)*px+sin(theta1)*py-a1; 
n=pz-d1;
H=(m^2+n^2-a2^2-a3^2-d4^2)/(2*a2);
theta3_1=atan2(H,sqrt(a3^2+d4^2-H^2))-atan2(a3,d4);
theta3_2=atan2(H,-sqrt(a3^2+d4^2-H^2))-atan2(a3,d4);

---

· 求解${\theta }_2$

关于\theta_2$的求解，我尝试了若干种方法。

♦ 机器人学导论的方法（失败的尝试）

首先，我按照《机器人学导论》（John J Craig）这本教材中记录的方法进行尝试。

众所周知，《机器人学导论》中都是以PUMA560为案例的，而PUMA560的结构与现在常用的工业机器人的构型并不相同（主要是和我研究的机器人不同），所以并不能直接拿来用。这里是参照其步骤进行计算的。

第一步，整理机器人末端位姿描述矩阵的计算式如下

$$[{}_3^{0}T\left({\theta }_2\right){]}^{-1}{}_6^{0}T={}_4^{3}T\left({\theta }_4\right){}_5^{4}T\left({\theta }_5\right){}_6^{5}T\left({\theta }_6\right)$$

令等号两边矩阵元素（1,4）和（2,4）相等，得到如下等式
$$\begin{gathered} (p_z-d_1)\sin ({\theta }_{23})-a_1\cos ({\theta }_{23})-a_2\cos ({\theta }_3)+... \\ {p}_x\cos ({\theta }_1)\cos ({\theta }_{23})+p_y\sin ({\theta }_1)\cos ({\theta }_{23})=a_3 \\ (p_z-d_1)\cos ({\theta }_{23})+a_1\sin ({\theta }_{23})+a_2\sin ({\theta }_3)-... \\ {p}_y\cos ({\theta }_1)\cos ({\theta }_{23})+p_x\sin ({\theta }_1)\cos ({\theta }_{23})=-d_4 \end{gathered}$$

---

• 计算过程如下

syms Q1 Q2 Q3 Q4 Q5 Q6  d1 d4 dt a1 a2 a3  nx ny nz ox oy oz ax ay az px py pz

%ZK-500连杆间齐次变换矩阵
T_01 =[ cos(Q1),   -sin(Q1),    0,      0
        sin(Q1),    cos(Q1),    0,      0
        0,          0,          1,      d1
        0,          0,          0,      1];
T_12 =[ cos(Q2),   -sin(Q2),    0,      a1
        0,          0,         -1,      0
        sin(Q2),    cos(Q2),    0,      0
        0,          0,          0,      1];
T_23 =[ cos(Q3),   -sin(Q3),    0,      a2
        sin(Q3),    cos(Q3),    0,      0
        0,          0,          1,      0
        0,          0,          0,      1];
T_34 =[ cos(Q4),   -sin(Q4),    0,      a3
        0,          0,         -1,     -d4
        sin(Q4),    cos(Q4),    0,      0
        0,          0,          0,      1];
T_45 =[ cos(Q5),   -sin(Q5),    0,      0
        0,          0,          1,      0
       -sin(Q5),   -cos(Q5),    0,      0
        0,          0,          0,      1];
T_56 =[ cos(Q6),   -sin(Q6),    0,      0
        0,          0,         -1,      0
        sin(Q6),    cos(Q6),    0,      0
        0,          0,          0,      1];
T_6t=[  1           0           0       0
        0           1           0       0
        0           0           1       dt
        0           0           0       1];

% 计算T_06和T_16的逆矩阵
T_06=[nx ox ax px;ny oy ay py;nz oz az pz;0 0 0 1];
T_03=T_01*T_12*T_23;
T_36=T_34*T_45*T_56;


% 计算T_01的逆矩阵
T_03_inv = inv(T_03);  

%输出结果并化简
T_left=T_03_inv*T_06;
disp("等式左边矩阵：")
%T_left=simplify(T_left)
T_left
disp("等式右边矩阵：")
simplify(T_36)

结果如下

T_left =
 
[nz*cos(Q2)*sin(Q3) + nz*cos(Q3)*sin(Q2) - nx*cos(Q1)*sin(Q2)*sin(Q3) - ny*sin(Q1)*sin(Q2)*sin(Q3) + nx*cos(Q1)*cos(Q2)*cos(Q3) + ny*cos(Q2)*cos(Q3)*sin(Q1),

 oz*cos(Q2)*sin(Q3) + oz*cos(Q3)*sin(Q2) - ox*cos(Q1)*sin(Q2)*sin(Q3) - oy*sin(Q1)*sin(Q2)*sin(Q3) + ox*cos(Q1)*cos(Q2)*cos(Q3) + oy*cos(Q2)*cos(Q3)*sin(Q1), 

az*cos(Q2)*sin(Q3) + az*cos(Q3)*sin(Q2) - ay*sin(Q1)*sin(Q2)*sin(Q3) + ax*cos(Q1)*cos(Q2)*cos(Q3) + ay*cos(Q2)*cos(Q3)*sin(Q1) - ax*cos(Q1)*sin(Q2)*sin(Q3), 

pz*sin(Q2 + Q3) - d1*sin(Q2 + Q3) - a1*cos(Q2 + Q3) - a2*cos(Q3) + (px*cos(Q1 + Q2 + Q3))/2 + (py*sin(Q1 + Q2 + Q3))/2 + (px*cos(Q2 - Q1 + Q3))/2 - (py*sin(Q2 - Q1 + Q3))/2]

[nz*cos(Q2)*cos(Q3) - nz*sin(Q2)*sin(Q3) - ny*cos(Q2)*sin(Q1)*sin(Q3) - ny*cos(Q3)*sin(Q1)*sin(Q2) - nx*cos(Q1)*cos(Q2)*sin(Q3) - nx*cos(Q1)*cos(Q3)*sin(Q2),

 oz*cos(Q2)*cos(Q3) - oz*sin(Q2)*sin(Q3) - oy*cos(Q2)*sin(Q1)*sin(Q3) - oy*cos(Q3)*sin(Q1)*sin(Q2) - ox*cos(Q1)*cos(Q2)*sin(Q3) - ox*cos(Q1)*cos(Q3)*sin(Q2),

 az*cos(Q2)*cos(Q3) - az*sin(Q2)*sin(Q3) - ax*cos(Q1)*cos(Q2)*sin(Q3) - ax*cos(Q1)*cos(Q3)*sin(Q2) - ay*cos(Q2)*sin(Q1)*sin(Q3) - ay*cos(Q3)*sin(Q1)*sin(Q2), 

pz*cos(Q2 + Q3) - d1*cos(Q2 + Q3) + a1*sin(Q2 + Q3) + a2*sin(Q3) + (py*cos(Q1 + Q2 + Q3))/2 - (px*sin(Q1 + Q2 + Q3))/2 - (py*cos(Q2 - Q1 + Q3))/2 - (px*sin(Q2 - Q1 + Q3))/2]

[
nx*sin(Q1) - ny*cos(Q1),
ox*sin(Q1) - oy*cos(Q1),
ax*sin(Q1) - ay*cos(Q1),
px*sin(Q1) - py*cos(Q1)
]

[0,0,0, 1]
 
等式右边矩阵：
[
cos(Q4)*cos(Q5)*cos(Q6) - sin(Q4)*sin(Q6),
- cos(Q6)*sin(Q4) - cos(Q4)*cos(Q5)*sin(Q6), 
cos(Q4)*sin(Q5),  
a3
]


[                          
cos(Q6)*sin(Q5),                            
-sin(Q5)*sin(Q6),        
-cos(Q5), 
-d4]

[cos(Q4)*sin(Q6) + cos(Q5)*cos(Q6)*sin(Q4),   
cos(Q4)*cos(Q6) - cos(Q5)*sin(Q4)*sin(Q6), 
sin(Q4)*sin(Q5),   
0]
[0, 0, 0, 1]

然后让ChatGPT帮我化简

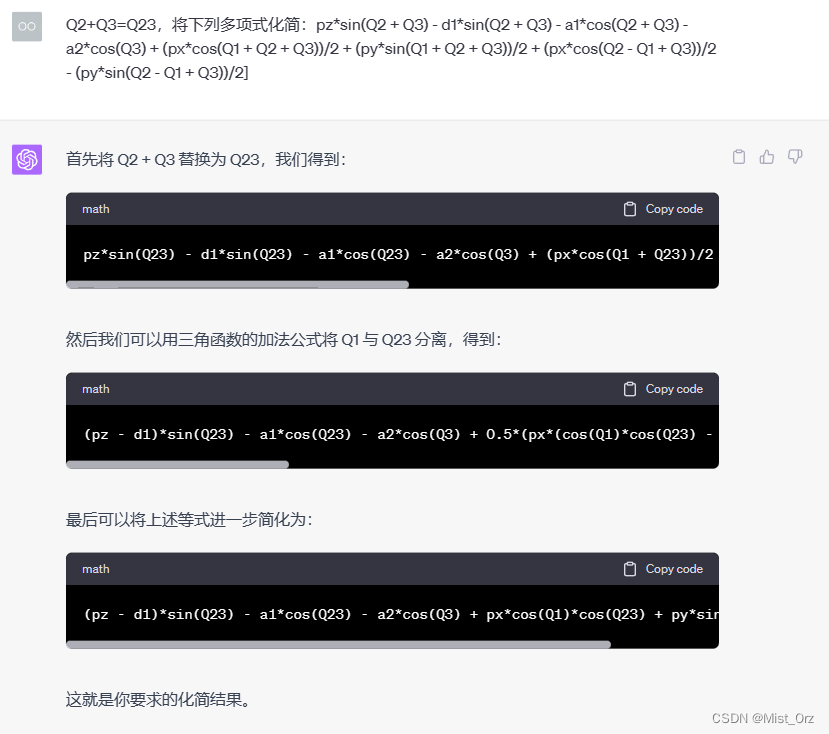
最后结果就是这个

(pz - d1)*sin(Q23) - a1*cos(Q23) - a2*cos(Q3) + px*cos(Q1)*cos(Q23) + py*sin(Q1)*cos(Q23)=a3;
(pz - d1)*cos(Q23) + a1*sin(Q23) + a2*sin(Q3) - py*cos(Q1)*cos(Q23) + px*sin(Q1)*cos(Q23)=-d4;

---

此时等式中未知的只有$s_{23}$和$c_{23}$，将其设为未知数，(理论上）就可以解出来${\theta }_2+{\theta }_3$

设
$$\begin{gathered} m_1=c_1{p}_x+s_1{p}_y-a_1 \\ {m}_2=p_z-d_1 \\ {m}_3=a_3+a_2{c}_3 \end{gathered}$$

$$\begin{gathered} n_1=-c_1{p}_y-s_1{p}_x-d_1 \\ {n}_2=a_1 \\ {n}_3=-d_4-a_2{s}_3 \end{gathered}$$

将方程组整理为
$$\begin{gathered} m_1{c}_{23}+m_2{s}_{23}=m_3 \\ {n}_1{c}_{23}+n_2{s}_{23}=n_3 \end{gathered}$$

解得

$$\begin{gathered} x=s_{23}=(m_1{n}_3-m_3{n}_1)/(m_1{n}_2-m_2{n}_1) \\ y=c_{23}=-(m_2{n}_3-m_3{n}_2)/m_1{n}_2-m_2{n}_1) \end{gathered}$$

于是
$${\theta }_{23}=Atan2(y,x)$$

然后再根据${\theta }_3$的取值得到${\theta }_2$

【！！？？】起来没问题，但是算出来的结果却和预设的值不同，不知道是哪里出了问题，如果有大佬看出来了希望能指点一二。

---

• matlab代码实现

m1=cos(theta1)*px+sin(theta1)*py-a1;
m2=pz-d1;
m3=a3+a2*cos(theta3);

n1=-cos(theta1)*py-sin(theta1)*px+pz-d1;
n2=a1;
n3=-d4-a2*sin(theta1);

x = (m1*n3 - m3*n1)/(m1*n2 - m2*n1);
y = -(m2*n3 - m3*n2)/(m1*n2 - m2*n1);

theta23=atan2(y,x)-pi/2;%这里减pi/2因为在DH参数中theta2补偿了pi/2

---

♦ 参考的文章中的方法（失败的尝试）

也就是前面提到的这篇文章：

→→→【MD-H模型运动学正解、逆解及姿态角的解算验证】

这篇文章中作者没有给出具体的推导过程，只给了matlab代码，代码如下

%theta2
c3=cosd(Theta3);s3=sind(Theta3);
g1=f2-d6*f1;
g2=f3-d6*az;
g3=a4*c3-d4*s3+a3;
Theta2=(atan2(g3,sqrt(g1^2+g2^2-g3^2))-atan2(g2,g1))*180/pi;
————————————————
版权声明：本文为CSDN博主「Vittore-Li」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/Vittore_Li/article/details/123185721

【！】注意，这篇文章作者的DH参数的定义和我是不一样的，我的a1=他的a2，我的a2=他的a3，我的a3=他的a4，另外他的DH模型的连杆的Z轴和我的方向是相反的，不知道会在求解中有什么影响。

我看了半天没看明白这是怎么来的，然后直接运行得到的结果也不正确（在针对我的DH模型做了相应修改后运行的）。

如果有哪个大佬知道作者用的是什么方法希望不吝赐教！（抱拳）

---

♦ 一个大佬的论文的方法（可以得到正确结果的方法）

是的，就是我前面（上一篇）说的那个大佬的论文，其实我前面的过程基本（或者说全部）也是按照大佬的步骤写的，只是加上了我的理解和验证过程。

大佬就是不一样，用的方法都是我没见过的。。。

机器人末端位置（坐标系6的原点）如下：

$$\begin{gathered} p_x=a_1{c}_1+a_3{c}_1{c}_{23}+d_4{c}_1{s}_{23}+a_2{c}_1{c}_2 \\ {p}_y=a_1{s}_1+a_3{s}_1{c}_{23}+d_4{s}_1{s}_{23}+a_2{c}_2{s}_1 \\ {p}_z=d_1+a_2{s}_2+a_3{s}_{23}-d_4{c}_{23} \end{gathered}$$

整理可得：

$$\begin{gathered} \frac{p_x}{c_1}-a_1=a_3{c}_{23}+d_4{s}_{23}+a_2{c}_2 \\ \frac{p_y}{s_1}-a_1=a_3{c}_{23}+d_4{s}_{23}+a_2{c}_2 \\ {p}_z-d_1=a_2{s}_2+a_3{s}_{23}-d_4{c}_{23} \end{gathered}$$

记

$$k_1=\frac{p_x}{c_1}-a_1{k_2=p}_z-d_1$$

得到：

$$\begin{gathered} k_1-a_2{c}_2=a_3{c}_{23}+d_4{s}_{23} \\ {k}_2-a_2{s}_2=a_3{s}_{23}-d_4{c}_{23} \end{gathered}$$

求平方和：

$$a_3^2+d_4^2=k_1^2+k_2^2+a_2^2-2k_1{a}_2{c}_2-2k_2{a}_2{s}_2$$

记

$$k_3=\left(k_1^2+k_2^2+a_2^2-a_3^2-d_4^2\right)/2a_2$$

则：

$$k_1{c}_2+k_2{s}_2=k_3$$
解得：
$${\theta }_2=Atan2\left(k_3,\pm \sqrt{k_1^2+k_2^2-k_3^2}\right)-Atan2\left(k_1,k_2\right)$$

---

• matlab代码实现

k1=px/cosd(theta(1))-a1;
k2=pz-d1;
k3=(k1^2+k2^2+a2^2-a3^2-d4^2)/(2*a2);

theta2_1=atan2(k3,sqrt(k1^2+k2^2-k3^2))-atan2(k1,k2)-pi/2;
theta2_2=atan2(k3,-sqrt(k1^2+k2^2-k3^2))-atan2(k1,k2)-pi/2;

---

❤ 2023.6.21 ❤

以上就是用代数解的方法求前三个轴的角度，按照一般流程，这个时候应该求后四个轴了，但是作为一篇总结方法型的文章，我是不满足于只记录一种实现方法的。

在学习了师弟的方法之后，我觉得用集合法解前三个轴应该是更简单的，至少和脑筋急转弯一样的代数法相比更好理解。

○ 几何解求${\theta }_1$、${\theta }_2$、${\theta }_3$

· 求解${\theta }_1$

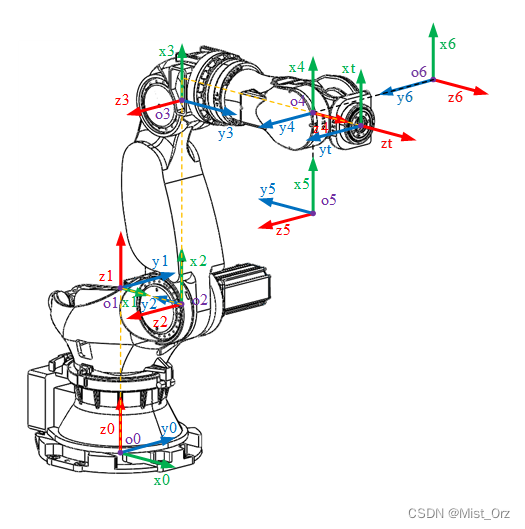
由机器人示意图可知，此构型的机器人，杆1、杆2、杆3组成的机构在同一竖直平面内，同时机器人末端为杆4、杆5、杆6坐标系的共同原点。由此可知，已知机器人末端坐标$\left(p_x,p_y,p_z\right)$即可求得轴1的转角${\theta }_1$

$${\theta }_1=Atan2\left(p_y,p_x\right)$$

甚至不用考虑多解的情况

---

· 求解${\theta }_3$