本文首发于算法社区,转载请注明出处,谢谢。
前言
倒谱的内容比较少,比较相关的就是同态系统去卷积了,所以把这两个放在一起了。
倒谱
我们考虑一个具有
z
z
z 变换的序列
{
x
n
}
\left \{ x_{n} \right \}
{xn} 。我们假设
{
x
n
}
\left \{ x_{n} \right \}
{xn} 是一个稳定的序列,那么
X
(
z
)
X\left ( z \right )
X(z) 在单位圆上是收敛的。这个序列
{
x
n
}
\left \{ x_{n} \right \}
{xn} 的复数倒谱(complex cepstrum)被定义为序列
c
x
(
n
)
c_{x}\left ( n \right )
cx(n)
,它是
C
x
(
z
)
C_{x}\left ( z \right )
Cx(z)的
z
z
z逆变换,其中
C
x
(
z
)
=
l
n
X
(
z
)
C_{x}\left ( z \right ) =lnX\left ( z \right )
Cx(z)=lnX(z)
如果
C
x
(
z
)
C_{x}\left ( z \right )
Cx(z)收敛于环域
r
1
<
∣
z
∣
<
r
2
r_{1}< |z|< r_{2}
r1<∣z∣<r2,其中
0
<
r
1
<
1
,
r
2
>
1
0< r_{1}< 1,r_{2}>1
0<r1<1,r2>1
倒谱的概念就这样完了_
同态去卷积
我们假设
{
y
(
n
)
}
\left \{ y\left ( n \right ) \right \}
{y(n)} 是线性时不变系统的输出序列,该系统由输入序列
{
x
n
}
\left \{ x_{n} \right \}
{xn} 激励。那么
Y
(
z
)
=
X
(
z
)
H
(
z
)
Y\left ( z \right ) = X\left ( z \right ) H\left ( z \right )
Y(z)=X(z)H(z)
其中
H
(
z
)
H\left ( z \right )
H(z) 是系统函数。对
Y
(
z
)
Y\left ( z \right )
Y(z) 取对数:
C
y
(
z
)
=
ln
Y
(
z
)
=
ln
X
(
z
)
+
ln
H
(
z
)
=
C
x
(
z
)
+
C
h
(
z
)
\begin{align} C_{y}\left ( z \right ) & = \ln_{}{} Y\left ( z \right ) \\ & = \ln_{}{} X\left ( z \right ) + \ln_{}{} H\left ( z \right ) \\ & = C_{x}\left ( z \right ) + C_{h}\left ( z \right ) \end{align}
Cy(z)=lnY(z)=lnX(z)+lnH(z)=Cx(z)+Ch(z)
因此,输出序列
{
y
(
n
)
}
\left \{ y\left ( n \right ) \right \}
{y(n)} 的复数倒谱表示为
{
x
n
}
\left \{ x_{n} \right \}
{xn} 的倒谱和
{
h
n
}
\left \{ h_{n} \right \}
{hn} 的倒谱之和,也就是
c
y
(
n
)
=
c
x
(
n
)
+
c
h
(
n
)
c_{y}\left ( n \right ) = c_{x}\left ( n \right ) + c_{h}\left ( n \right )
cy(n)=cx(n)+ch(n)
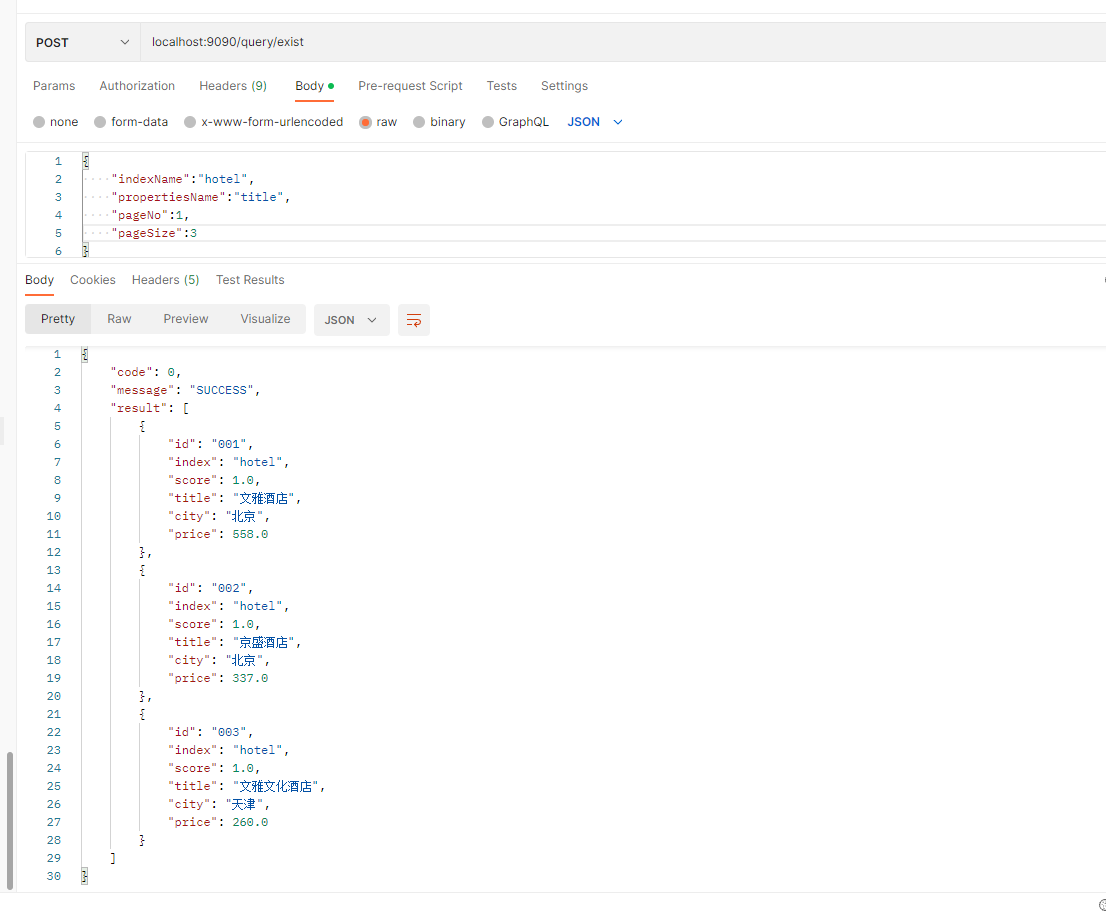
这样我们注意到在时域两个序列的卷积对应于倒谱域的倒谱序列之和。执行这些变换的系统称为同态系统(homormorphic system),如图 2-1 所示。

图 2-1 获得序列
{
y
(
n
)
}
\left \{ y\left ( n \right ) \right \}
{y(n)} 的倒谱
c
y
(
n
)
c_{y}\left ( n \right )
cy(n)
应用说明
在一些应用中,比如地震信号处理和语音信号处理,倒谱序列
{
c
x
(
n
)
}
\left \{ c_{x}\left ( n \right ) \right \}
{cx(n)} 和
{
c
h
(
n
)
}
\left \{ c_{h}\left ( n \right ) \right \}
{ch(n)} 的特性是足以不同的以至于它们在倒谱域中可被分离。特别地,假设
{
c
x
(
n
)
}
\left \{ c_{x}\left ( n \right ) \right \}
{cx(n)} 在
n
n
n小值附近拥有它的主要成份(主要能量),而
{
c
h
(
n
)
}
\left \{ c_{h}\left ( n \right ) \right \}
{ch(n)}拥有集中在
n
n
n大值处成份。我们可能说 是“低通”和 是“高通”。那么我们可以使用合适的 “低通” 窗和 “高通” 窗从
{
c
x
(
n
)
}
\left \{ c_{x}\left ( n \right ) \right \}
{cx(n)}分离
{
c
h
(
n
)
}
\left \{ c_{h}\left ( n \right ) \right \}
{ch(n)},如图 3-1 所示。
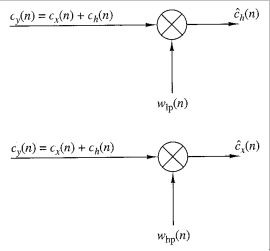
图 3-1 通过“低通”和“高通”窗口分离这两个倒谱成份
这样:
c
^
h
(
n
)
=
c
y
(
n
)
ω
l
p
(
n
)
\hat{c}_{h}\left ( n \right ) = c_{y}\left ( n \right ) \omega_{lp}\left ( n \right )
c^h(n)=cy(n)ωlp(n)
和
c
^
h
(
n
)
=
c
y
(
n
)
ω
h
p
(
n
)
\hat{c}_{h}\left ( n \right ) = c_{y}\left ( n \right ) \omega_{hp}\left ( n \right )
c^h(n)=cy(n)ωhp(n)
其中
ω
l
p
(
n
)
=
{
1
,
∣
n
∣
≤
N
1
0
,
∣
n
∣
>
N
1
\omega_{lp}\left ( n \right )=\begin{cases}1,|n|\le N_{1} \\ 0,|n|> N_{1} \end{cases}
ωlp(n)={1,∣n∣≤N10,∣n∣>N1,
ω
h
p
(
n
)
=
{
0
,
∣
n
∣
≤
N
1
1
,
∣
n
∣
>
N
1
\omega_{hp}\left ( n \right )=\begin{cases}0,|n|\le N_{1} \\ 1,|n|> N_{1} \end{cases}
ωhp(n)={0,∣n∣≤N11,∣n∣>N1
一旦我们通过窗口分离了倒谱序列
{
C
^
h
(
n
)
}
\left \{ \hat{C}_{h}\left ( n \right ) \right \}
{C^h(n)} 和
{
C
^
x
(
n
)
}
\left \{ \hat{C}_{x}\left ( n \right ) \right \}
{C^x(n)},那么把
{
C
^
h
(
n
)
}
\left \{ \hat{C}_{h}\left ( n \right ) \right \}
{C^h(n)} 和
{
C
^
x
(
n
)
}
\left \{ \hat{C}_{x}\left ( n \right ) \right \}
{C^x(n)} 通过逆同态系统,就可得到序列
{
x
^
(
n
)
}
\left \{ \hat{x}\left ( n \right ) \right \}
{x^(n)} 和
{
h
^
(
n
)
}
\left \{ \hat{h}\left ( n \right ) \right \}
{h^(n)},如图 3-2。

图 3-2 从相应倒谱恢复序列
{
x
n
}
\left \{ x_{n} \right \}
{xn} 和
{
h
n
}
\left \{ h_{n} \right \}
{hn} 的逆同态系统
小结
虽然倒谱和同态系统的基本知识差不多讲完了,但肯定还有东西可以挖,还需要继续深入。我倒是想知道那些前辈们是怎么提出倒谱这个参量的,除了倒谱说不定还有我们暂时未知的其他谱