图像直方图
在统计学中,直方图是一种对数据分布情况的图形化表示方法。
图像直方图是用来表示数字图像中亮度分布的直方图,使用图像直方图可以很直观地观察到该图的亮度分布情况。在图像直方图中,横轴从左到右分别表示了从纯黑到纯白区域的亮度值的分布。
横坐标:图像中各个像素点的灰度级。
纵坐标:在该像素灰度的像素的个数。
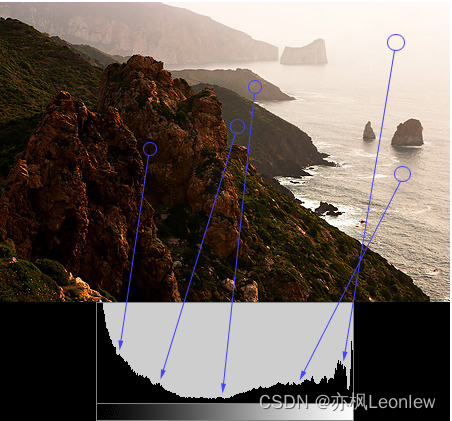
原图:Understanding Digital Camera Histograms: Tones and Contrast
如上图所示,从这张图片的直方图我们可以很清楚地看到。图片中像素亮度分布情况是在左右两端分布多,中间分布少。较暗的像素占比较大。
我们以一个非常简单的例子来看直方图如何绘制,假设有一张3x3的图片,各个像素的灰度值如下:

可以看到,像素有5种灰度值(x),因此横坐标我们设置为5个单位;y表示每种灰度值的像素个数统计,根据直方图的定义我们绘制出这个3x3图片的折线直方图为:
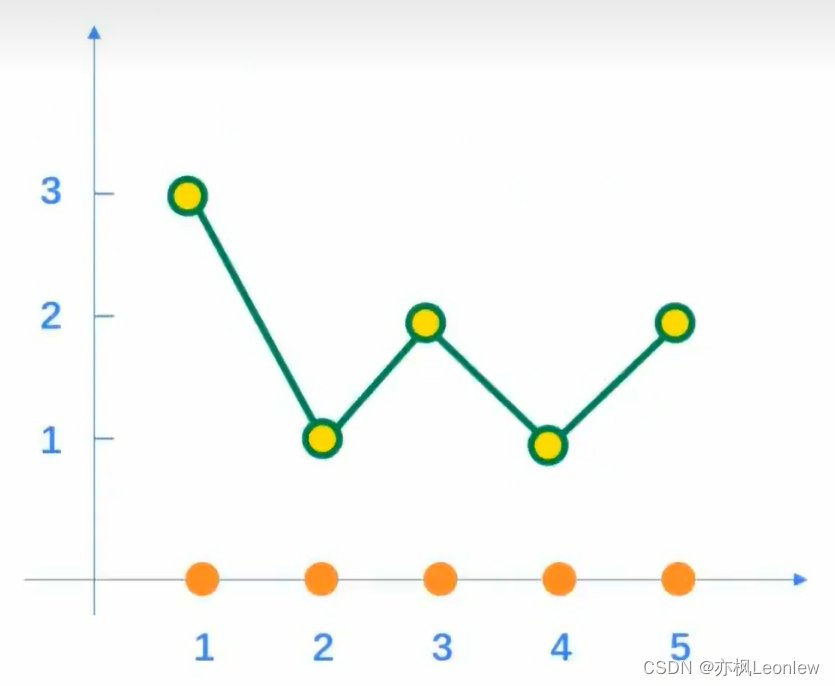
用柱状直方图表示如下:
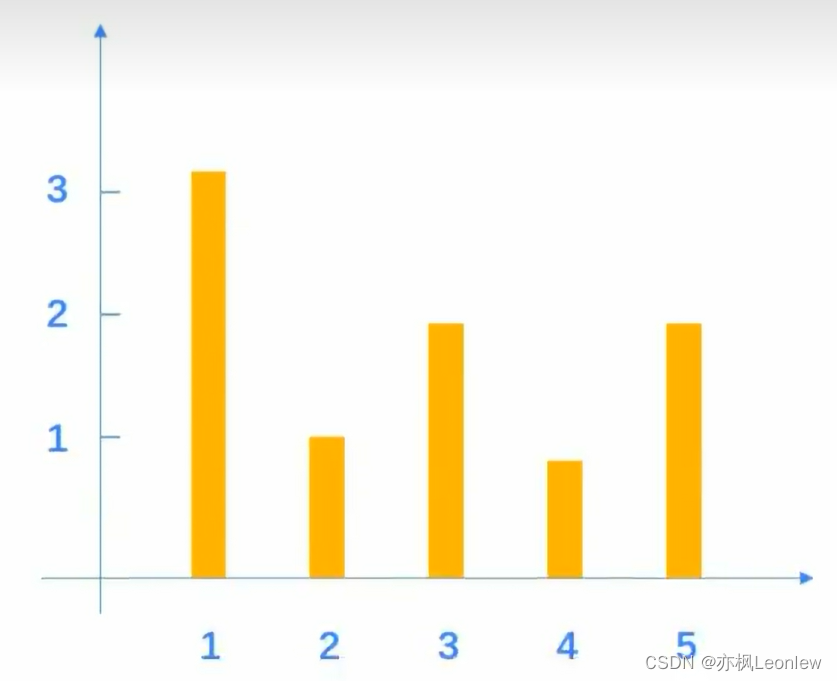
这两种图本质上是没有区别的, 另外还可以用归一化的直方图来表示。
归一化直方图的横轴仍然是像素的灰度级,但纵轴表示的是对应灰度级像素个数在图片中所占的比例。

对应的归一化直方图(折线)绘制出来如下:
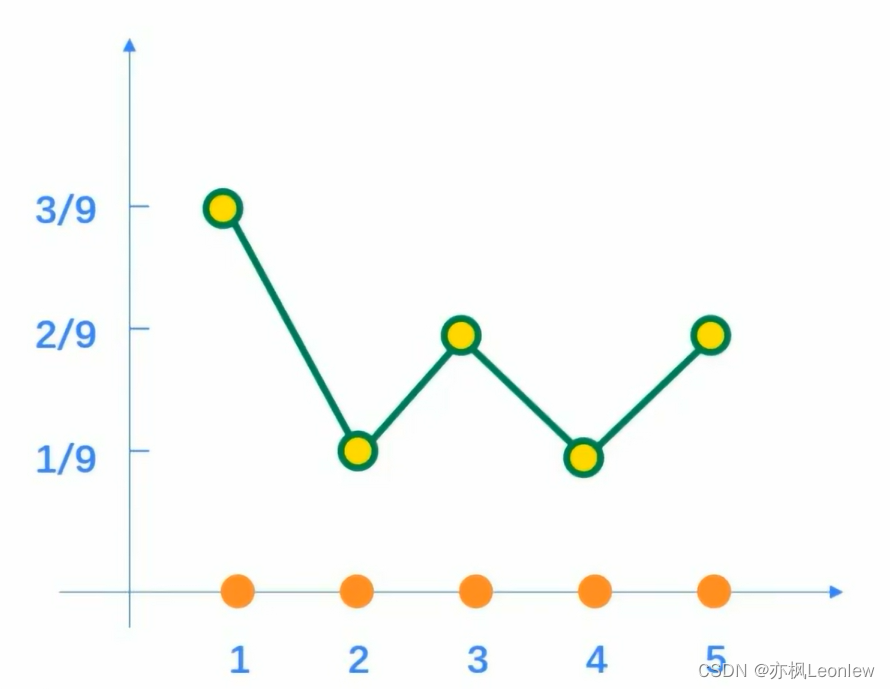
下面再来看一个实际的例子:
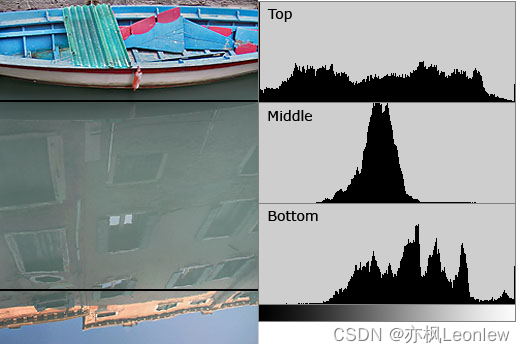
从这三张直方图来看,顶部图片的直方图较为均衡,看起来效果比较正常;中间图片亮度分布集中在中间区域,且中心较为密集,图片看起来对比度不高,整体偏灰;底部图片的直方图在较暗区域基本没有像素,较亮区域分布较少,整体稍微偏向亮区多一点,分布也不均匀。一般来说,除了一些特殊场景,第一种直方图分布均衡的视觉效果更好。
直方图的一些术语
dims:需要统计的特征的数量。例如dims = 1表示只统计灰度值。
bins: 每个特征空间子区段的数量。
range:灰度值的范围,一般为[0,255]。
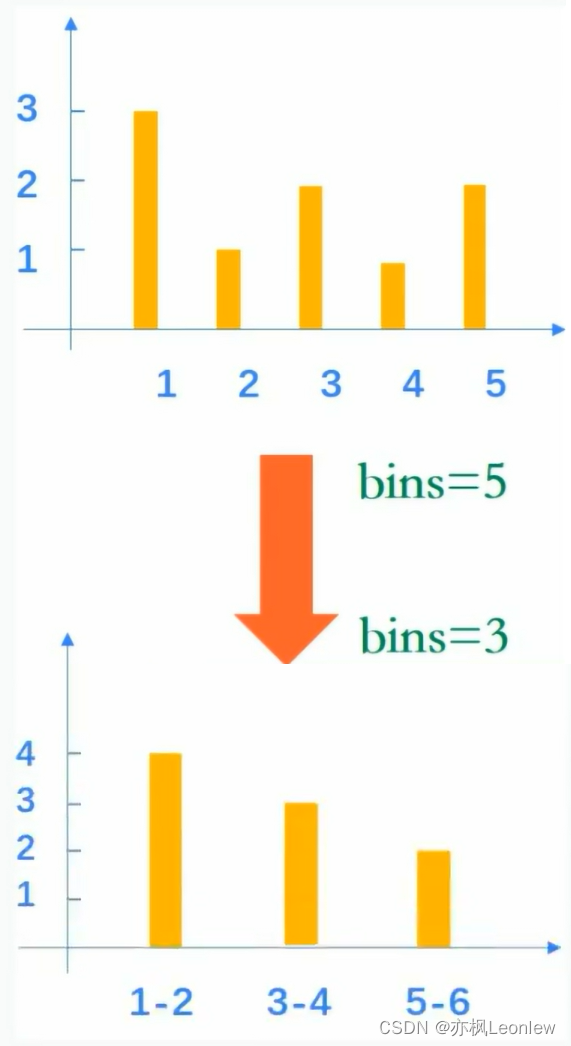
如上图,最初bins = 5,我们将bins设置为3,将像素灰度级变为3个范围(bins),每个范围包含两个灰度级。统计每个灰度范围内的像素个数并绘制出来。
对于bins,下图是另一个例子:
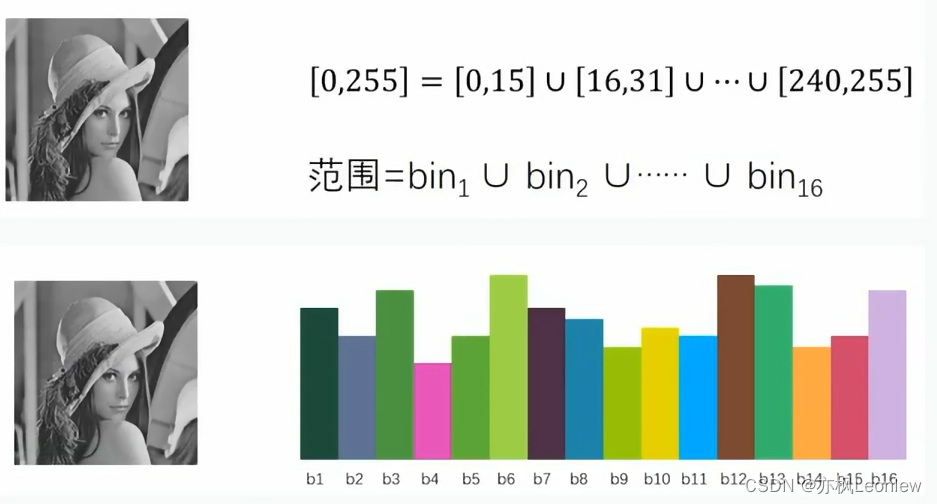
直方图均衡化
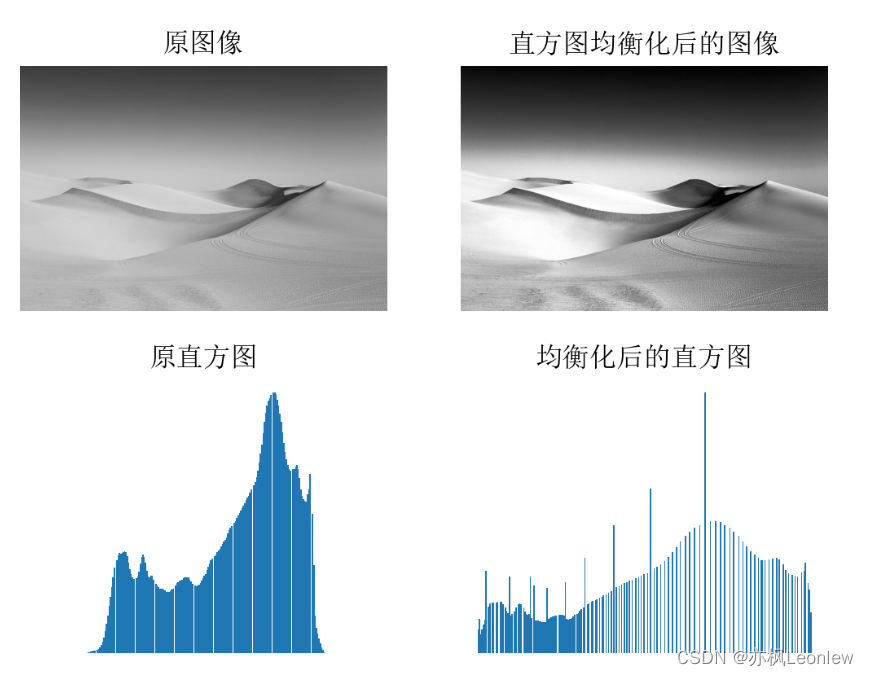
直方图均衡化是通过调整像素亮度分布范围,让像素在[0.255]灰阶上分布地更加均匀,从而提高图像的对比度,改善图像视觉效果。一般对于对比度较低的图像,直方图均衡化比较适合,会增强图像细节。
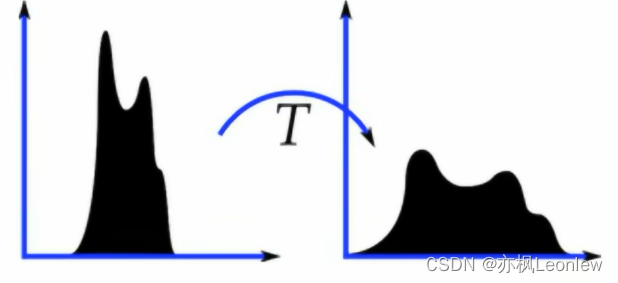
扩展原图的亮度范围的操作,从数学上看,我们需要一个映射函数,将原图的像素值均衡映射到新的直方图中,这个函数要满足两个条件:
1. 不打乱原有像素值大小顺序,映射后亮、暗的大小关系不能变。
2. 映射后的像素值在原来的像素值范围内(一般是[0,255])。
做直方图均衡的时候,会使用累积分布函数,因为累计分布函数是单调递增且最大值为1,能够保证上述两个太哦啊金。关于直方图均衡和累计分布函数关系推导,可以参考这篇文章:
数字图像处理:直方图均衡(Histogram Equalization)的原理及处理介绍_LaoYuanPython的博客-CSDN博客本文介绍了《数字图像处理》第三章直方图均衡的主要知识点,直方图均衡法针对非数字图像以及数字图像都存在通用的公式,只需要数字图像和非数字图像自身的信息,二者虽然由于灰度值连续和离散的不同公式有所不同,但本质是一致的。本文的介绍是完全基于《数字图像处理》的介绍,其中有些内容对于不熟悉数字图像处理的人员理解可能存在困难,请等待老猿后续的系列博文答疑解惑。_直方图均衡https://blog.csdn.net/LaoYuanPython/article/details/119857829
累积分布函数
图像由离散的像素点组成,因此图像直方图均衡化通过离散形式的累积分布函数求解。直方图均衡化过程中,映射方法是:
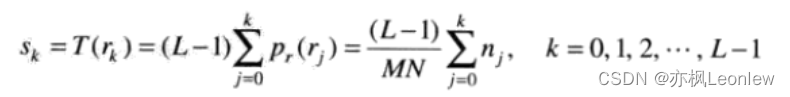
是指经过累计分布函数映射后的灰度值;
MN是像素的个数;
表示灰度为j的像素个数;
L表示灰度级的数量(8 bit的像素值有256个灰度级)
直方图均衡化过程
1. 计算原图的统计直方图
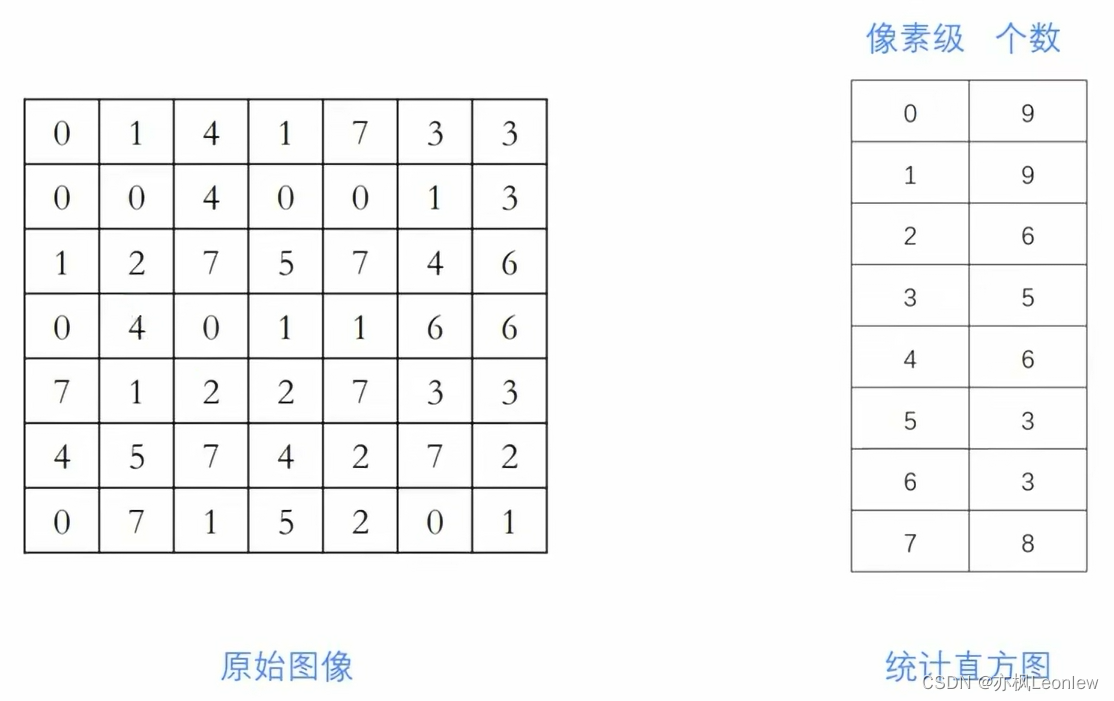
2. 根据统计直方图得到归一化直方图,通过归一化直方图得到累计直方图
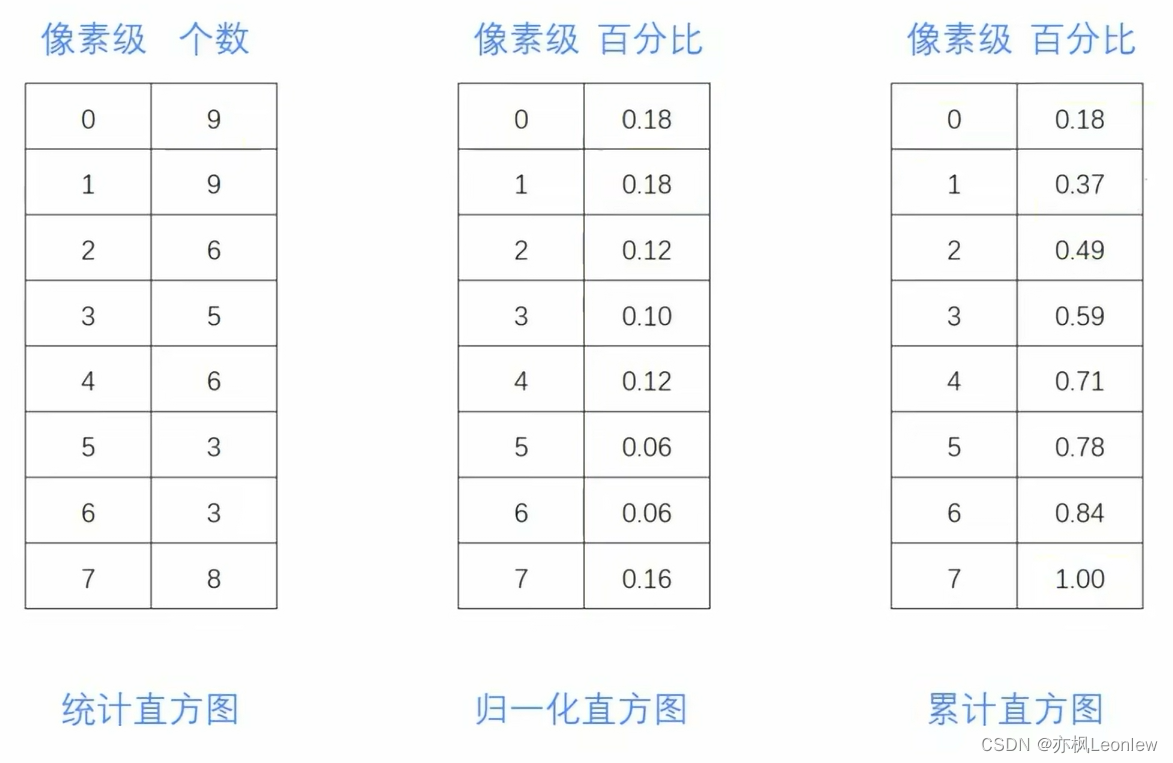
可以看到,累计直方图的像素级对应的值是这个像素级本身像素出现的概率加上之前所有像素级出现概率的和(图中像素级1对应的值是0.37是因为归一化直方图中未显示第三位小数点,理解过程即可)。
3. 使用累计直方图做区间转换

根据离散累计分布函数的公式计算。案例中有8个像素级,因此L - 1 = 7。用累计概率乘以(L - 1)就得到了
。对比一下原始直方图和均衡直方图:
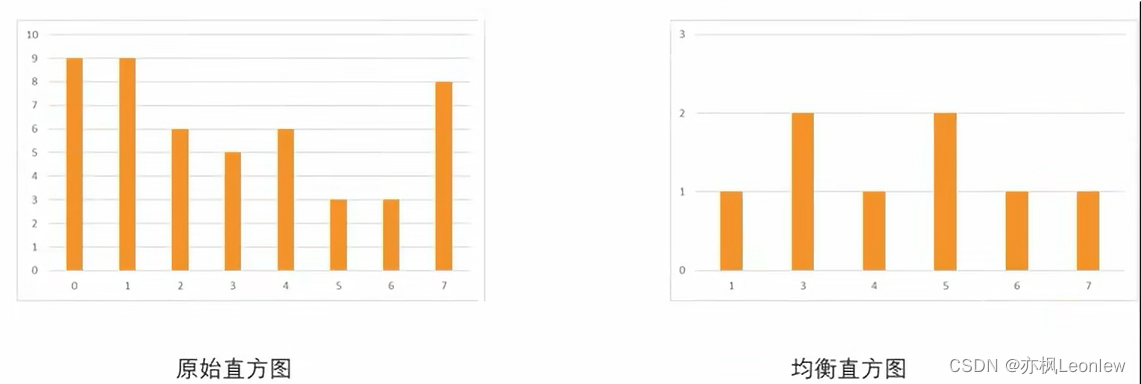
最后,来看一个实际的直方图均衡化的例子: