10.1 k近邻学习

k近邻学习（kNN）是一种常用的监督学习方法，其工作机制非常简单：给定测试样本，基于某种距离度量找出训练集中与其最靠近的k个训练样本，然后基于这k个邻居的信息来进行预测。
k近邻学习似乎与之前的学习方法相比有一个明显的不同之处：它似乎没有显式的训练过程！它是懒惰学习的著名代表，此类学习技术在训练阶段仅仅是把样本保存起来，训练时间开销为0，待收到测试样本后再进行处理；相应的，那些在训练阶段就对样本进行学习处理的方法称为急切学习。
下图给出了k近邻分类器的一个示意图，显然k是一个重要的参数，当k取不同值时，分类结果会有显著不同。另一方面，若采用不同的距离计算方式，则找出的“近邻”可能有显著差别，从而也会导致分类结果有显著不同。

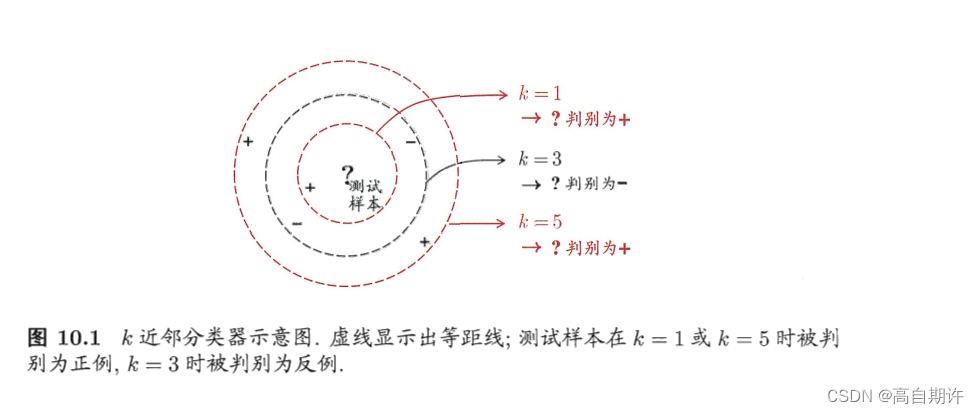
下面给出一个重要结论，最近邻分类器虽简单，但它的泛化错误率不超过贝叶斯最优分类器的错误率的两倍。

10.2 低维嵌入

上一节的讨论是基于一个重要假设：任意测试样本x附近任意小的距离范围内总能找到一个训练样本，即训练样本的采样密度足够大，或称为密采样。事实上，在高维情形下出现的数据样本稀疏、距离计算困难等问题，是所有机器学习方法共同面临的严重障碍，被称为维数灾难。
缓解维数灾难的一个重要途径是降维，亦称维数约简，即通过某种数学变换将原始高维属性空间转变为一个低维子空间，在这个子空间中样本密度大幅提高，距离计算也变得更为容易。

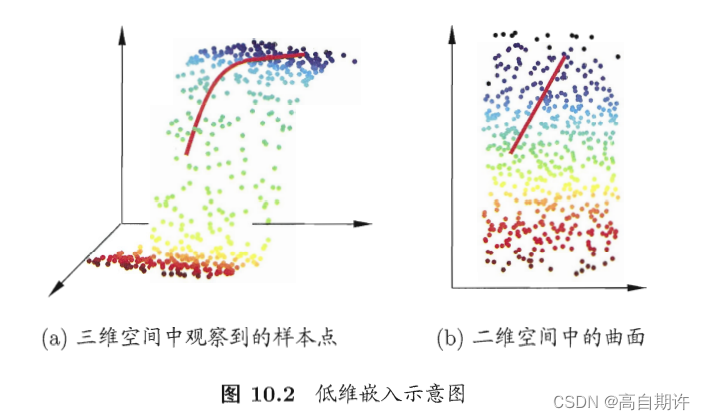
若要求原始空间中样本之间的距离在低维空间中得以保持，如上图所示，即得到多维缩放（Multiple Dimensional Scaling，简称MDS）。

10.3 主成分分析

主成分分析（Principal Component Analysis，简称PCA）是最常用的一种降维方法。在介绍PCA之前，不妨先考虑这样一个问题：对于正交属性空间中的样本点，如何用一个超平面对所有样本进行恰当的表达？
PCA算法如下图所示：

10.4 核化线性降维

线性降维方法假设从高维空间到低维空间的函数映射是线性的，然而，在不少现实任务中，可能需要非线性映射才能找到恰当的低维嵌入。下图给出一个例子，样本点从二维空间中的矩形区域采样后以S形曲面嵌入到三维空间，若直接使用线性降维方法对三维空间观察到的样本点进行降维，则将丢失原本的低维结构。为了对原本采样的低维空间与降维后的低维空间加以区别，我们称前者为本真低维空间。

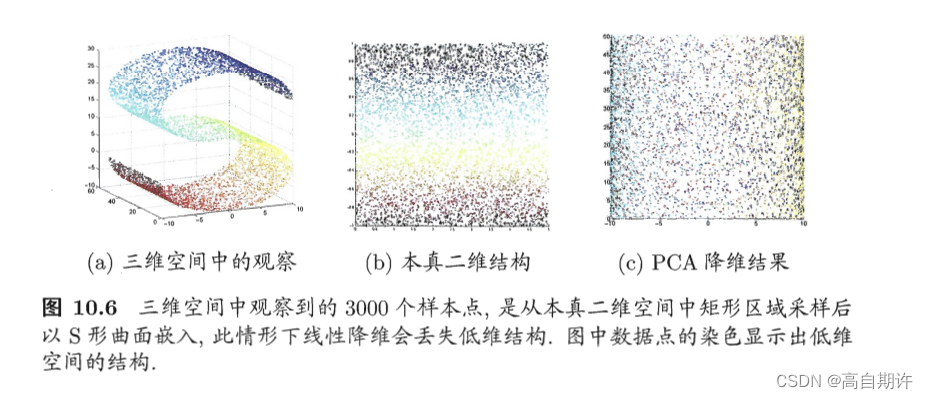
非线性降维的一种常用方法，是基于核技巧对线性降维方法进行核化，有一种经典方法叫核主成分分析（KPCA）。

10.5 流形学习

流形学习是一类借鉴了拓扑流形概念的降维方法。“流形”实在局部与欧氏空间同胚的空间，换言之，它在局部具有欧氏空间的性质，能用欧氏距离来进行距离计算。这给降维方法带来了很大的启发：若低维流形嵌入到高维空间中，则数据样本在高维空间的分布虽然看上去非常复杂，但在局部上仍具有欧氏空间的性质，因此，可以容易地在局部建立降维映射关系，然后再设法将局部映射关系推广到全局。当维数被降至二维或三维时，能对数据进行可视化展示，因此流形学习也可被用于可视化。

10.5.1 等度量映射

等度量映射（Isometric Mapping，简称Isomap）的基本出发点，是认为低维流形嵌入到高维空间之后，直接在高维空间中计算直线距离具有误导性，因为高维空间中的直线距离在低维嵌入流形上是不可达的。如图所示：

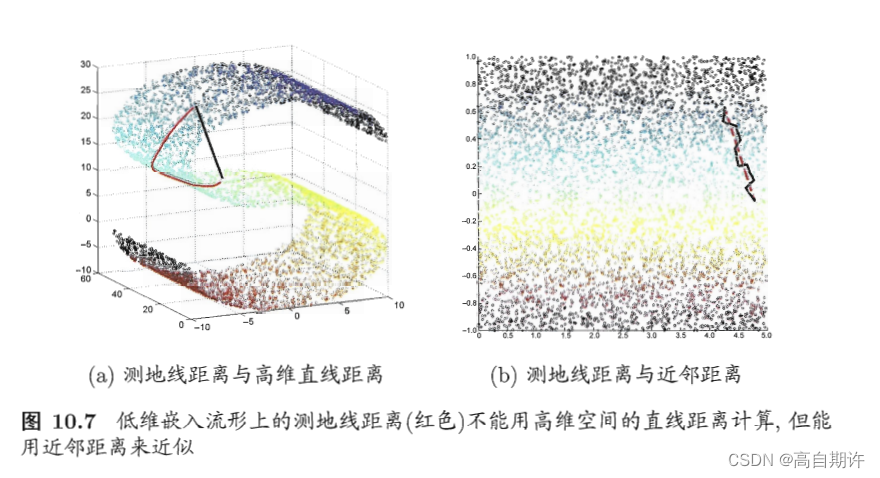
图a中，低维嵌入流形上两点间的距离是测地线距离：想像一只虫子从一点爬到另一点，如果它不能脱离曲面行走，那么图啊中的红色曲线就是距离最短的路径，即S曲面上的测地线，测地线距离是两点之间的本真距离。显然直接在高维空间中计算直线距离是不恰当的。
下面给出Isomap算法的基本描述：

10.5.2 局部线性嵌入

与Isomap试图保持临近样本之间的距离不同，局部线性嵌入（Locally Linear Embedding，简称LLE）试图保持邻域内样本之间的线性关系，如图所示：

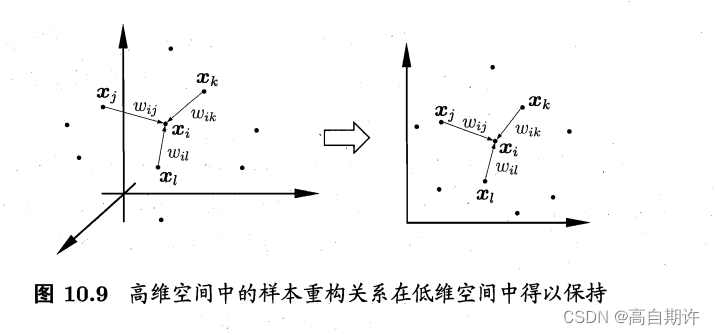
LLE的算法描述如图所示：

10.6 度量学习

在机器学习中，对高维数据进行降维的主要目的是希望找到一个合适的低维空间，再此空间中进行学习能比原始空间性能更好。事实上，每个空间对应了在样本属性上定义的一个距离度量，而寻找合适的空间，实质上就是在寻找一个合适的距离度量。直接尝试学习出一个合适的距离度量就是度量学习的基本动机。