目录

 1. 两数相加（2）

2. 寻找两个正序数组的中位数（4）

---

1. 两数相加（2）

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

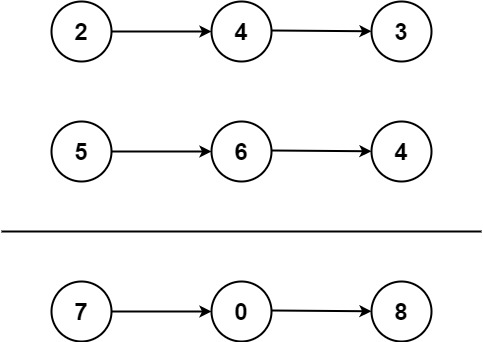
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

解法思路(O(max(m,n))):因为这是一个单链表,不可逆向查找,只能从头找到尾.所以首先,我们需要设置一个头指针和尾指针.让他们同指向同一个链表,然后需要一个临时变量来存储每一位的和.实现代码如下.

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode head=null,node=null;
        int temp=0;
        while(l1!=null||l2!=null){
            if(l1==null){
                l1=new ListNode(0);
            }
            if(l2==null){
                l2=new ListNode(0);
            }
            temp=l1.val+l2.val+temp;
            if(head==null){
                head=node=new ListNode(temp%10);
            }else{
                node.next=new ListNode(temp%10);
                node=node.next;
            }
            temp=temp/10;
            l1=l1.next;
            l2=l2.next;
        }
        if(temp>0){
            node.next=new ListNode(temp);
        }
        return head;
    }
}

2. 寻找两个正序数组的中位数（4）

 

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

解法思路:这个题可以采用归并排序的思路，首先需要设置一个空数组，临时变量和两个指针，

因为给出的两个数组都是有序数组，所以可以从两个数组的首端开始比较，较小的放入新数组，具体实现代码如下。

参考文章：算法 - 归并排序（Merge_sort）_曾铎000811的博客-CSDN博客

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int[] result=new int[nums1.length+nums2.length];
        int temp=0,i=0,j=0;
        double mid=0;
        while(i<nums1.length||j<nums2.length){
            if(i<nums1.length&&j<nums2.length){
                if(nums1[i]<nums2[j]){
                    result[temp]=nums1[i];
                    i++;
                }else if(nums2[j]<nums1[i]){
                    result[temp]=nums2[j];
                    j++;
                }else{
                    result[temp]=nums1[i];
                    temp++;
                    i++;
                    result[temp]=nums2[j];
                    j++;
                }
            }else if(i>=nums1.length){
                result[temp]=nums2[j];
                j++;
            }else{
                result[temp]=nums1[i];
                i++;
            }
            temp++;
        }
        if(result.length%2==0){
            mid=(result[result.length/2]+result[result.length/2-1])/2.0;
        }else{
            mid=result[(result.length+1)/2-1];
        }
        return mid;
    }
}