对于动态规划问题，我将拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

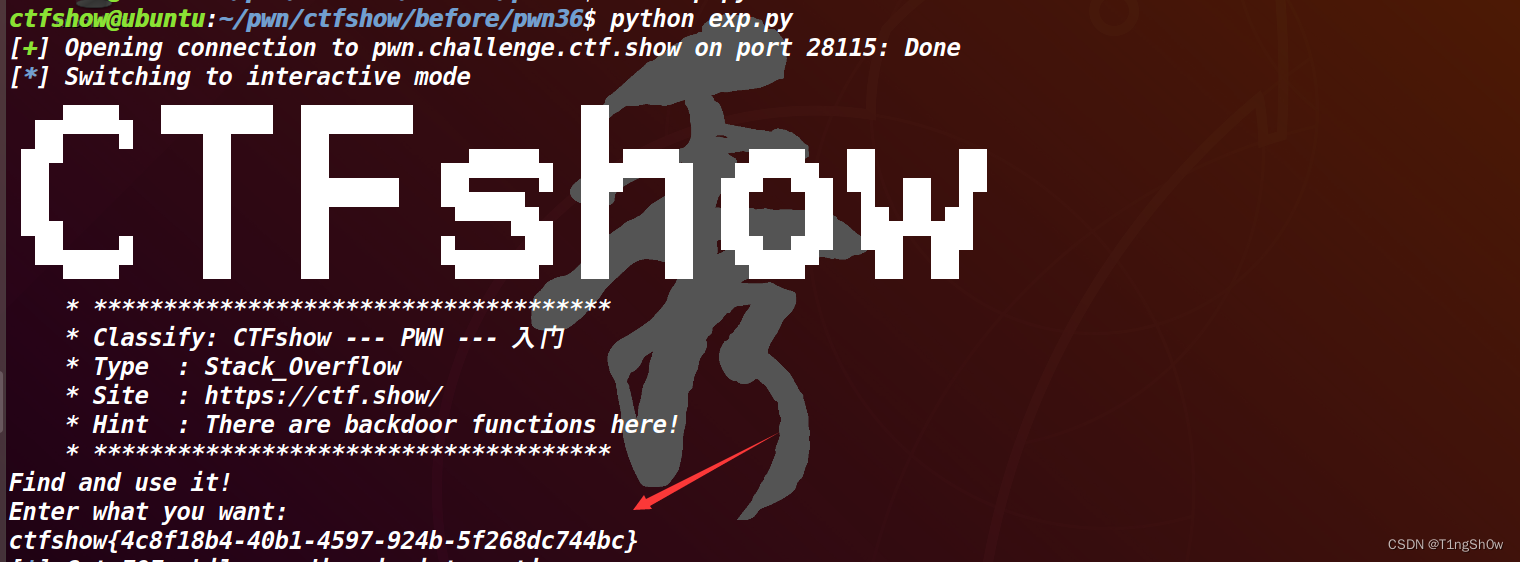
JZ42 连续子数组的最大和

思路：五部曲

1. 确定dp数组（dp table）以及下标的含义
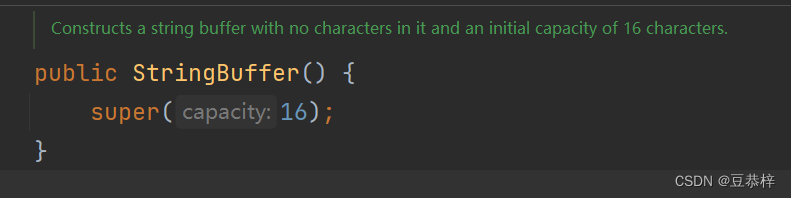
   dp[i]：包括下标i的最长连续子序和
2. 确定递推公式

• 加入当前array[i]的子序和 dp[i] = dp[i-1]+array[i]
• 当前元素 array[i]

3. dp数组如何初始化
   初始化dp[0] = array[0]
4. 确定遍历顺序
   dp的更新需要前一个dp信息，从前往后遍历

import java.util.*;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param array int整型一维数组 
     * @return int整型
     */
    public int FindGreatestSumOfSubArray (int[] array) {
        // write code here
        int result = array[0];//结果
        int[] dp = new int[array.length]; //dp数组
        dp[0]=array[0];
 
        for(int i=1;i<array.length;i++){
            //状态转移方程
            dp[i] = Math.max(dp[i-1]+array[i],array[i]);
            if(dp[i]>result){
                result = dp[i];
            }
        }
        return result;
    }
}

JZ85 连续子数组的最大和(二)

思路：动态规划部分和上题一致，该题需要存储最长的子数组。
使用两个指针来记录当前最大和的区间，再用两个指针记录最长的区间，每次更新max的时候更新区间。

import java.util.*;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param array int整型一维数组 
     * @return int整型一维数组
     */
    public int[] FindGreatestSumOfSubArray (int[] array) {
        // write code here

        int[] dp = new int[array.length];
        dp[0] = array[0];
        int max = array[0];
        
        int left=0,right=0;//滑动区间
        int resl=0,resr=0;//记录最长区间
        for(int i=1;i<array.length;i++){
            right++;
            dp[i] = Math.max(dp[i-1]+array[i],array[i]);
            if(array[i]>(dp[i-1]+array[i])){
                left=right;
            }

            if(dp[i]>max || dp[i]==max && (right-left+1)>(resr-resl+1)){ //记录最大和以及更新区间
                max = dp[i];
                resl=left;
                resr=right;
            }
        }
        int[] res = new int[resr-resl+1];
        for(int i=resl;i<=resr;i++){
            res[i-resl]=array[i];
        }
        return res;
    }
}

JZ69 跳台阶

思路：

1. dp[i]代表上i级台阶的跳法
2. dp[i] = dp[i-1]+dp[i-2]
3. dp[0]=1; dp[1]=1;
4. 从前往后遍历

import java.util.*;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param number int整型 
     * @return int整型
     */
    public int jumpFloor (int number) {
        // write code here
        int[] dp = new int[number+1];
        dp[0]=1;
        dp[1]=1;

        for(int i=2;i<=number;i++){
            dp[i] = dp[i-1]+dp[i-2];
        }
        return dp[number];
    }
}
JZ10 斐波那契数列
[图片]
import java.util.*;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param n int整型 
     * @return int整型
     */
    public int Fibonacci (int n) {
        // write code here
        if(n==1){
            return 1;
        }else if(n==2){
            return 1;
        }
        return Fibonacci(n-1)+Fibonacci(n-2);
    }
}

JZ71 跳台阶扩展问题

import java.util.*;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param number int整型 
     * @return int整型
     */
    public int jumpFloorII (int number) {
        // write code here
        int[] dp = new int[number+1];
        dp[0]=1;
        dp[1]=1;
        for(int i=2;i<=number;i++){
            dp[i] = 2*dp[i-1];
        }
        return dp[number];
    }
}

JZ70 矩形覆盖

import java.util.*;
public class Solution {
    public int rectCover(int target) {
        if(target<=2){
            return target;
        }
        return rectCover(target-1)+rectCover(target-2);
    }
}

---