我们知道队列这种数据结构的物理实现方式主要还是两种，一种是链队列（自定义节点类），另一种则是使用数组实现，两者各有优势。此处我们将要介绍的循环队列其实是队列的一种具体实现，由于一般的数组实现的队列结构在频繁出队的情况下，会产生假溢出现象，导致数组使用效率降低，所以引入循环队列这种结构。本文将从以下两个大角度介绍循环队列这种数据结构：

• 循环数组实现循环队列
• Java中具体实现容器类ArrayDeque

一、循环队列      为了深刻体会到循环队列这个结构优于非循环队列的地方，我们将首先介绍数组实现的非循环队列结构。队列这种数据结构，无论你是用链表实现，还是用数组实现，它都是要有两个指针分别指向队头和队尾。在我们数组的实现方式中，用两个int型变量用于记录队头和队尾的索引。

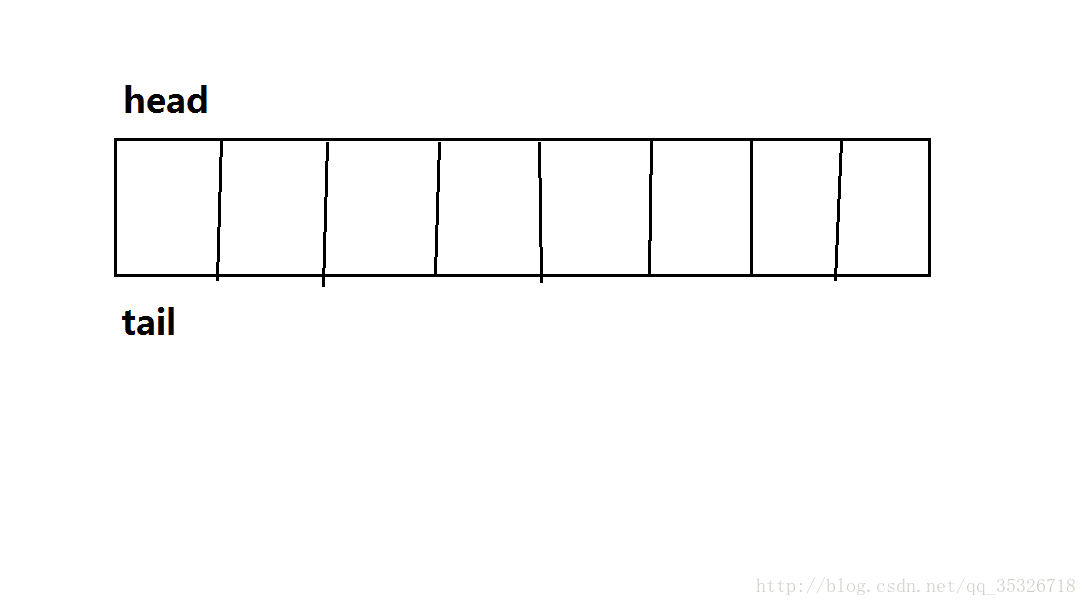
一个队列的初始状态，head和tail都指向初始位置（索引为0处）。head永远指向该队列的队头元素，tail则指向该队列最后一个元素的下一位置，当有入队操作时：

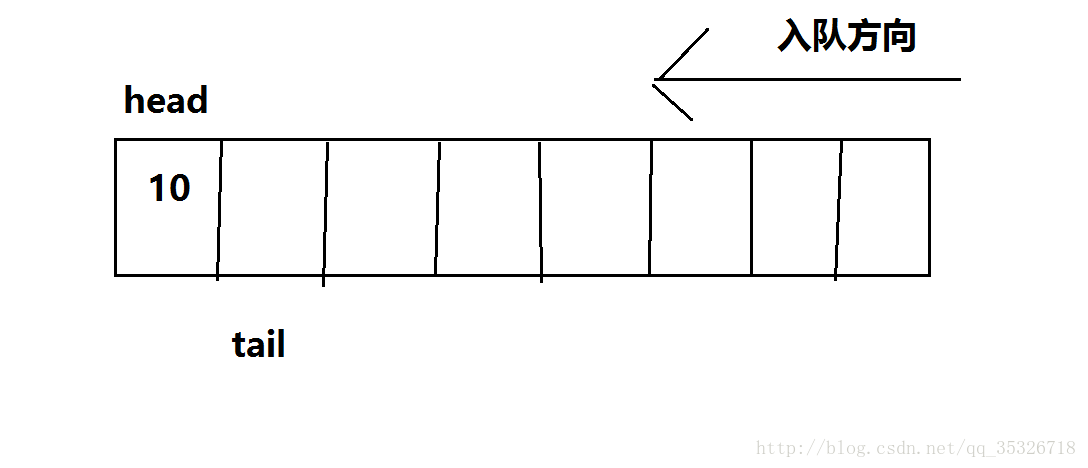
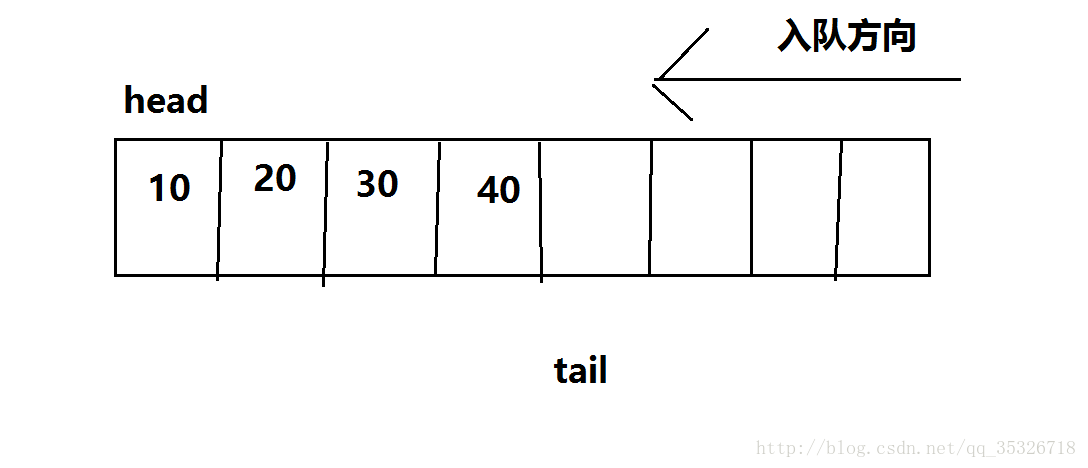
当有出队操作时：

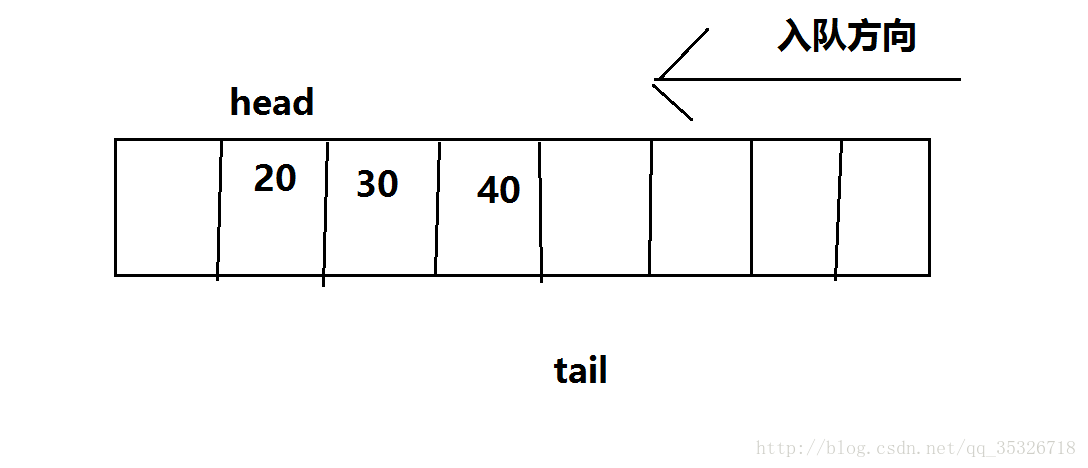
当遇到出队操作时，head会移向下一元素位置。当然，对于这种方式入队和出队，队空的判断条件显然是head=tail，队满的判断条件是tail=array.length（数组最后一个位置的下一位置）。显然，这种结构最致命的缺陷就是，tail只知道向后移动，一旦到达数组边界就认为队满，但是队列可能时刻在出队，也就是前面元素都出队了，tail也不知道。例如：

此时tail判断队满，我们暂时认为资源利用是可以接受的，但是如果接下来不断发生出队操作：

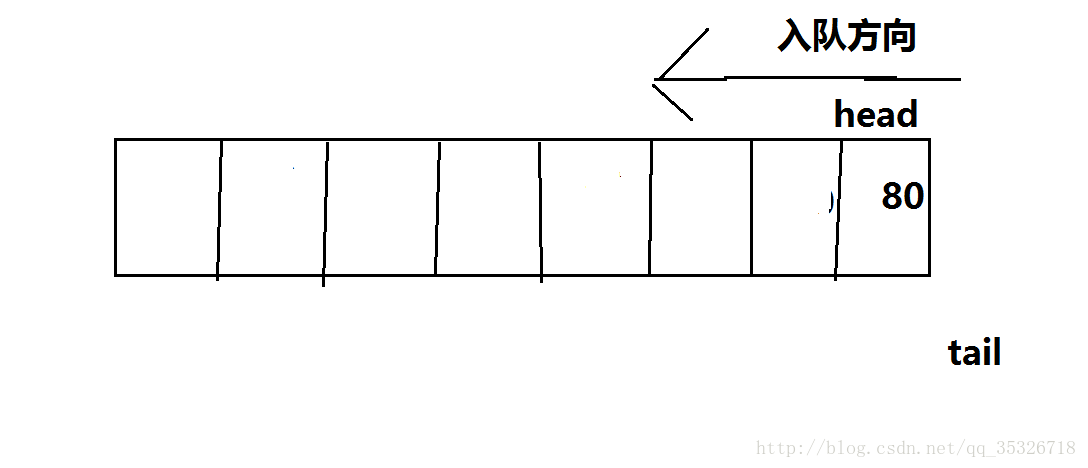
此时tail依然通过判断，认为队满，不能入队，这时数组的利用率我们是不能接受的，这样浪费很大。所以，我们引入循环队列，tail可以通过mode数组的长度实现回归初始位置，下面我们具体来看一下。

按照我们的想法，一旦tail到达数组边界，那么可以通过与数组长度取模返回初始位置，这种情况下判断队满的条件为tail=head

此时tail的值为8，取模数组长度8得到0，发现head=tail，此时认为队列满员。这是合理的，但是我们忽略了一个重要的点，判断队空的条件也是head=tail，那么该怎么区分是队空还是队满呢？解决办法是，空出队列中一个位置，如果(tail+1)%array.length=head，我们就认为队满，下面说明其合理性。

上面遇到的问题是，tail指向了队尾的后一个位置，也就是新元素将要被插入的位置，如果该位置和head相等了，那么必然说明当前状态已经不能容纳一个元素入队（间接的说明队满）。因为这种情况是和队空的判断条件是一样的，所以我们选择舍弃一个节点位置，tail指向下一个元素的位置，我们使用tail+1判断下一个元素插入之后，是否还能再加入一个元素，如果不能了说明队列满，不能容纳当前元素入队（其实还剩下一个空位置），看图：

tail通过取模，回归到初始位置，我们判断tail+1是否等于head，如果等于说明队满，不允许入队操作，当然这是牺牲了一个节点位置来实现和判断队空的条件进行区分。上述文字基本完成了队循环队列的理论介绍，下面我们看在Java中对该数据结构的具体实现是怎样的。

二、双端队列实现类ArrayDeque      ArrayDeque中主要有以下几个属性域：

transient Object[] elements;
transient int head;
transient int tail;
private static final int MIN_INITIAL_CAPACITY = 8;

复制

elements就是我们上述介绍用于存储队列中每个节点，不过在ArrayDeque中该数组长度是没有限制的，采用一种动态扩容机制实现动态扩充数组容量。head和tail分别代表着头指针和尾指针。MIN_INITIAL_CAPACITY 代表着创建一个队列的最小容量，具体使用情况在下文详细介绍。现在我们看下它的几个构造函数：

public ArrayDeque() {
    elements = new Object[16];
}
public ArrayDeque(int numElements) {
    allocateElements(numElements);
}

复制

如果没有指定显式传入elements的长度，则默认16。如果显式传入一个代表elements的长度的变量，那么会调用allocateElements做一些简单的处理，并不会简单的将你传入的参数用来构建elements，它会获取最接近numElements的2的指数值，比如：numElements等于20，那么elements的长度会为32，numElements为11，那么对应elements的长度为16。但是如果你传入一个小于8的参数，那么会默认使用我们上述介绍的静态属性值作为elements的长度。至于为什么这么做，因为这么做会大大提高我们在入队时候的效率，我们等会儿会看到。

入队操作 由于ArrayDeque实现了Deque，所以它是一个双向队列，支持从头部或者尾部添加节点，由于内部操作类似，我们只简单介绍从尾部添加入队操作。涉及以下一些函数：

public void addLast(E e) {
    if (e == null)
        throw new NullPointerException();
    elements[tail] = e;
    if ( (tail = (tail + 1) & (elements.length - 1)) == head)
    doubleCapacity();
}

public boolean offerLast(E e) {
    addLast(e);
    return true;
}

public boolean add(E e) {
    addLast(e);
    return true;
}

复制

显然，主要的方法还是addLast，其实有人可能会疑问，为什么要这么多重复的方法呢？其实，虽然我们这个ArrayDeque它实现了双端队列，并且我们本篇主要把他当做队列来研究，其实该类完全可以作为栈或者一些其他结构来使用，所以提供了一些其他的方法，但本质上还是某几个方法。此处我们主要研究下addLast这个方法，该方法首先将你要添加的元素入队，然后通过这条语句判断队是否已满：

if ( (tail = (tail + 1) & (elements.length - 1)) == head)

复制

这条语句的判断条件还是比较难理解的，我们之前在构造elements元素的时候，说过它的长度一定是2的指数级，所以对于任意一个2的指数级的值减去1之后必然所有位全为1，例如：8-1之后为111，16-1之后1111。而对于tail来说，当tail+1小于等于elements.length - 1，两者与完之后的结果还是tail+1，但是如果tail+1大于elements.length - 1，两者与完之后就为0，回到初始位置。这种判断队列是否满的方式要远远比我们使用符号%直接取模高效，jdk优雅的设计从此可见一瞥。接着，如果队列满，那么会调用方法doubleCapacity扩充容量，

private void doubleCapacity() {
    assert head == tail;
    int p = head;
    int n = elements.length;
    int r = n - p; 
    int newCapacity = n << 1;
    if (newCapacity < 0)
        throw new IllegalStateException("Sorry, deque too big");
    Object[] a = new Object[newCapacity];
    System.arraycopy(elements, p, a, 0, r);
    System.arraycopy(elements, 0, a, r, p);
    elements = a;
    head = 0;
    tail = n;
}

复制

该方法还是比较容易理解的，首先会获取到原数组长度，扩大两倍构建一个空数组，接下来就是将原数组中的内容移动到新数组中，下面通过截图演示两次移动过程：

这是一个满队状态，假如我们现在还需要入队，那么久需要扩容，扩容结果如下：

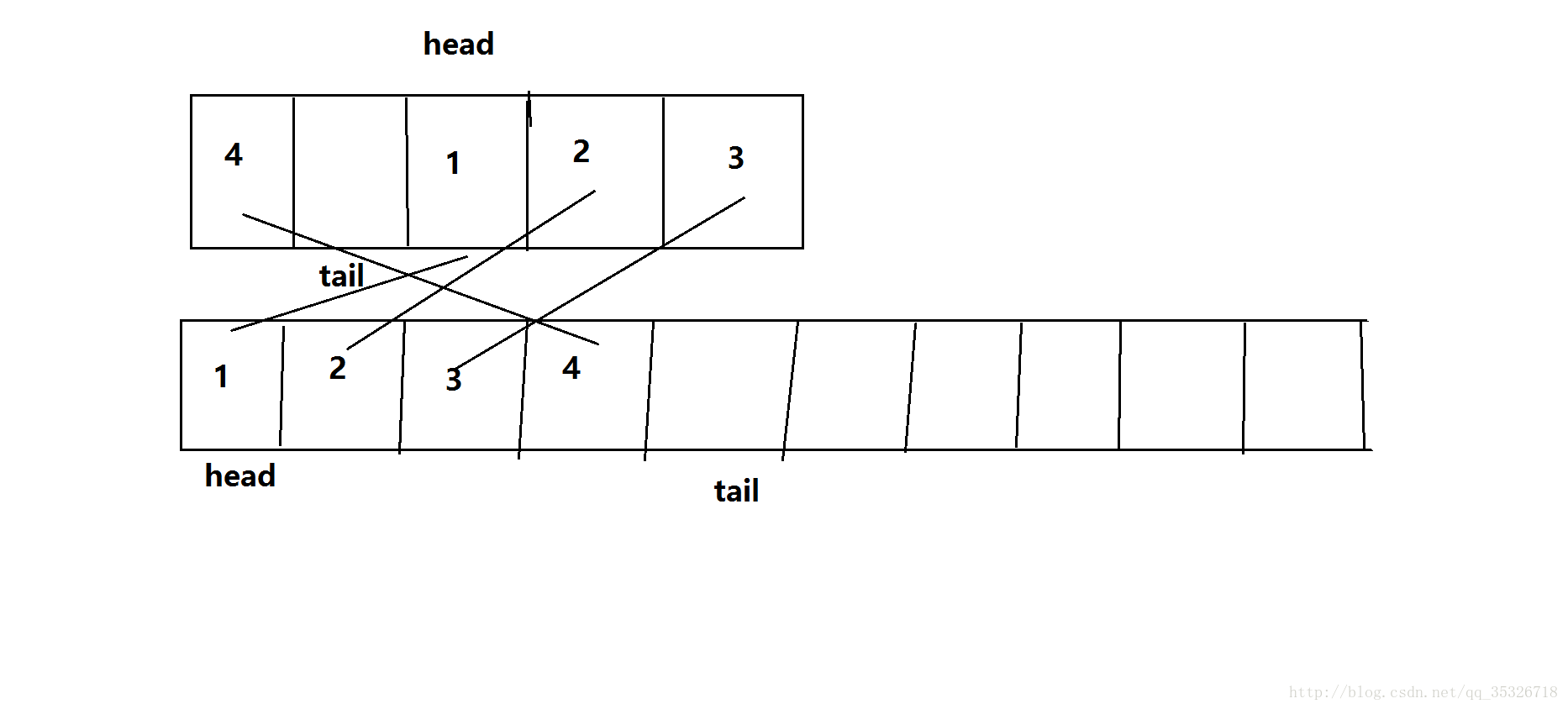
其实两次移动数组，第一次将head索引之后的所有元素移动到新数组中，第二次将tail到head之间的所有元素移动到新数组中。实际上，就是在移动的时候对原来的顺序进行了调整。对于addFirst只不过是将head向前移动一个位置，然后添加新元素。

出队操作 出队操作和入队一样，具有着多个不同的方法，但是内部调用的还是一个pollFirst方法，我们主要看下该方法的具体实现即可：

public E pollFirst() {
    int h = head;
    @SuppressWarnings("unchecked")
    E result = (E) elements[h];
    if (result == null)
        return null;
    elements[h] = null;
    head = (h + 1) & (elements.length - 1);
    return result;
}

复制

该方法很简单，直接获取数组头部元素即可，然后head往后移动一个位置。这是出队操作，其实删除操作也是一种出队，内部还是调用了pollFirst方法：

public E removeFirst() {
    E x = pollFirst();
    if (x == null)
        throw new NoSuchElementException();
    return x;
 }

复制

其他的一些操作 我们可以通过getFirst()或者peekFirst()获取队头元素（不删除该元素，只是查看）。toArray方法返回内部元素的数组形式。

public Object[] toArray() {
    return copyElements(new Object[size()]);
}

复制

还有一些利用索引或者值来检索具体节点的方法，由于这些操作并不是ArrayDeque的优势，此处不再赘述了。

至此，有关ArrayDeque的简单原理已经介该绍完了，ArrayDeque的主要优势在于尾部添加元素，头部出队元素的效率是比较高的，内部使用位操作来判断队满条件，效率相对有所提高，并且该结构使用动态扩容，所以对队列长度也是没有限制的。在具体情况下，适时选择。