引入

一、“思维方式”是解题关键！！

1、统计思维的诞生

2、概率的力量

概率与数理统计的区别？

如何验证假设？

经验与现实如何共存——贝叶斯定理？

“朴素”的朴素贝叶斯？

二、数据“陷阱”

1、数据收集的偏差

2、数据处理的悖论

3、正确解读数据

4、精准预测的挑战

总结

引入

本系列博客尝试讨论一些有关AI的通识问题，AI本身就是一个跨学科、专业、抽象、复杂的问题，学习相关专业知识可能会很困难，尤其是一些数学公式和复杂的程序代码。本系列博客以“机器智能”的底层逻辑为切入点，重点放在讨论AI的核心技术和原理上。本系列逻辑：

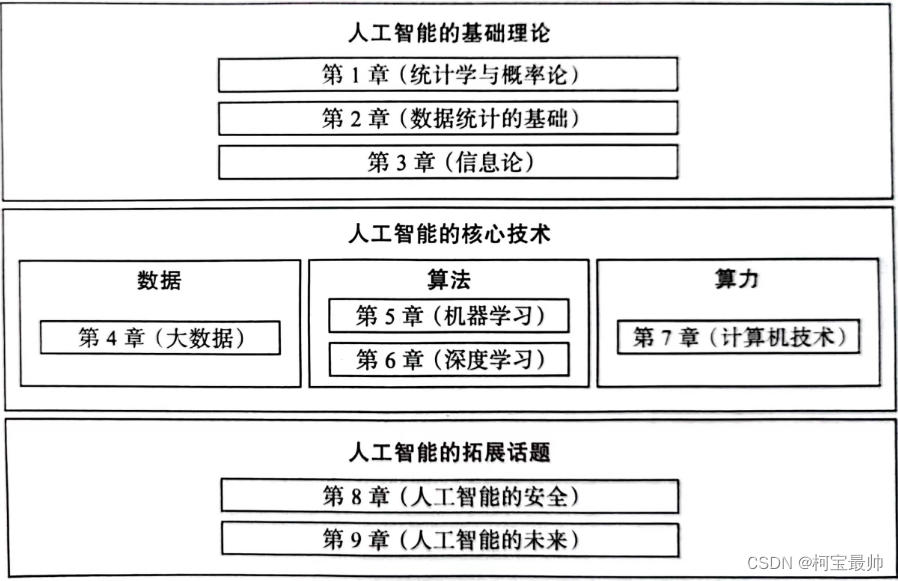
一、“思维方式”是解题关键！！

近年来AI的发展离不开高性能计算机及分布式技术、机器学习和ANN的发展、积累的大数据等，但最本质的因素是——思维方式的改变。解决人工智能问题本质是把现实中的应用场景问题转化为一个计算机可以处理的数学问题，这一步几乎占据了问题解决的一半。如今AI主要依赖的是数学工具和信息技术而不是医学等，这就是认知思维上的改变。

使机器智能化并不是列出所有的智力规则让计算机遵照执行，因为这样计算机永不会超出人的认知范围，实际上是让计算机从大量数据中自己“学习”规律，这也是思维上看待问题角度的一个改变——如何在充满不确定性的环境中解决比较确定的问题，于是一个重要的数学工具——“统计学”诞生了！

1、统计思维的诞生

以前的科学相信，这个世界存在简单而通用的真理，如欧几里得5条几何学真理、牛顿运动3定律、麦克斯韦4个电磁微分方程、爱因斯坦相对论等，所以科学家尝试用简洁的公式描述复杂世界的规律，即世界万物在一定先决条件下都具有可预测性——“决定论”！但是现在发现无法用简单几个公式描述世界的全部细节，越是微观越不确定，部分人转换思维创造了——“统计学”，它承认了不确定性的存在，接收误差对结果的影响，并把它们作为前提条件进行数学建模和分析！

统计学应用实例：利用放射性元素的半衰期和现在包含的放射量推测出地球的年龄！半衰期具有典型的统计学意义，体现了个体随机性和总体不确定性之间的联系，即——即便无法准确掌握每个个体的随机情况，但是可以利用统计规律来推算出总体状态！

严格来说统计和统计学在数学定义上时不同的，统计本质是一个数学过程，只要有数据就可统计，要处理的数据是确定的，如本月自己的开销总和，此过程不涉及统计学，不用对一些不确定性的情况进行推断。统计学则不同，是一门研究不确定性的学科，研究对象具有大量的随机性！——注意随机不是均匀。

2、概率的力量

概率与数理统计的区别？

概率论与数理统计时常被一起提及，但两者存在区别。概率论是统计学的基础，是对随机性进行数学研究的理论基础；数理统计则关注通过大量原始数据研究对象行为规律的方法——概率论更偏数学理论，数理统计更多的是应用！举例来说，概率论研究的是一个“白盒”，清楚盒子里几个红球几个白球（即已知数学上的分布函数），然后猜测摸到特定颜色球的可能；数理统计面对的是“黑盒”，只能看到每次从盒子里摸出来的是红球还是白球，然后猜测盒子中颜色的分布。前一个是参数估计，后一个称为假设检验！

随着重复试验次数的增大，事件的频率会呈现稳定性，这个频率常数近似可代表事件发生的可能性，即它的概率！这是一个比较抽象的概念，首先概率是个经验值，由频率推导而来；其次概率揭示了不确定性中的确定；概率避免不了“黑天鹅”数据（异常值）。重复试验的次数越多，得到的概率越让人信服，这依托于大数定律，定律表明样本数量越多，结论越接近真实的概率分布。如今经常提及的蒙特卡洛方法理论依据就是大数定律，原理很朴实：不断抽样逐次逼近，比如计算圆周率Π，就是利用计算机在正方形和圆中不断撒点，通过面积比和点的数量之间的关系计算！这能用于很多需要枚举的算法，如下围棋、走迷宫或计算任何不规则图形的面积等。

如何验证假设？

大数定理很有用但在现实生活中无法适用所有场景！某些时候我们只掌握了有限个“小数据”，但必须马上做出判断，这时通常的做法是先提出一些假设，然后想办法验证它们是否合理——即假设检验。基本思想是先假设它成立看会产生什么后果，当观测结果出现的概率很低时可拒绝此假设；方法是反证法，是一种推翻既定假设的工具，假设检验就是一种在待检验假设成立时计算观测结果出现概率的统计方法！

举例，手里有一组数据但是不清楚总体分布函数，又或者只知道它的数学分布形式，但不确定具体参数。此时为了推断总体分布的某些特性，可先假设总体服从泊松分布，或者假设服从正态分布的总体的数学期望是某个值等。随后根据手上的样本数据，判断这些假设是要接收还是拒绝，假设检验就是这样一个决策过程！它也称显著性检验，“显著”一词表示概率足够低足以拒绝假设。

进行参数估计时，除了想知道参数的平均值，也关心精确程度（区间），即置信区间。

在已知总体数学分布形式但不知具体参数时，可用Z检验法、T检验法、F检验法来判断假设是否足以拒绝！实际上我们不知道总体服从何种分布，这时需要根据样本来检验假设的分布，常用卡方检验法，实际值与期望值如果相同，卡方值为0，两者相差越大卡方值越大。

经验与现实如何共存——贝叶斯定理？

想象这样一种情形，我们知道的概率统计与现实生活出现冲突，或者说前人的经验不符合自己亲身经历，即出现了理论与现实的矛盾。举个例子，如猜硬币正反面，按理说每次正反面的概率都是0.5，可以随便猜总会猜对一半，但是那毕竟是理论你无法保证眼前这枚硬币确实如此，如一枚硬币抛了10次有8次都是正面，那么下次你就应该猜正面！即根据历史经验不断修正自己认知，此思考方式背后的数学原理是贝叶斯定理！

贝叶斯定理蕴含了一种解决问题的框架思路：不断地通过增加信息和经验，逐步逼近真相或理解未知。它的过程可归纳为：“过去的经验”+“新的证据”得到“修正后的判断”，提供了一种将新观察到的证据和已有的经验相结合进行推断的客观方法。引入了条件概率关系：后验概率P(A|B)=先验概率P(A)xP(B|A)/P(B)。先验概率一般是由以往的数据分析或统计得到的概率数据，后验概率是在某些条件下发生的概率，是在得到信息后重新加以修正的概率。当先验概率足够强大时，即使出现新的证据，先验概率也会有惊人影响力，所以要全局来看！

贝叶斯定理帮助我们，基于少量数据做出最合适的推理和判断！

“朴素”的朴素贝叶斯？

贝叶斯定理研究的是条件概率，也即在特定条件下的概率问题。基于此思想，人们提出了朴素贝叶斯算法。朴素贝叶斯常解决分类问题，目的在于把具有某些特征的样本划分到最可能属于的类别，也就是样本属于哪个类别的概率最大，就认为它属于哪个类别。如邮件分类、文章分类、情感分析等。

它“朴素”在哪儿？即满足一个基本假设：假设给定目标的各个特征之间是相互独立的，即条件独立性。这是因为如果每个特征不是相互独立的，在计算概率时，必须把这些特征的所有排列组合都考虑一遍，计算量大甚至产生指数级参数数量，实际执行难度很大！有时忽略一些条件之间的关联性得到的结论与实际不会有太大偏差。

二、数据“陷阱”

上面我们知道了人工智能的解题思路——统计思维！！不过统计学高质量的数据，AI运作的基础也是数据，如果数据错误或者对数据的理解出现偏差，将直接导致结论谬误。有时数据具有欺骗性和迷惑性，使用时需要对它们进行甄别！！

1、数据收集的偏差

收集数据的质量直接关乎分析结论的成败，但错误的收集方法会导致结果偏差。如统计对象出现错误、统计对象不全面只抽取部分数据等，这些会导致两种常见的数据偏差——幸存者偏差和选择性偏差。幸存者偏差是由于没有准确选择研究对象的偏差，提醒我们要考察所有类型的数据；选择性偏差是由于没有“公平”地挑选数据导致的偏差，提醒我们要客观地挑选数据。两者都未看清数据全貌，导致“以偏概全”。

2、数据处理的悖论

我们习惯使用统计数据来简化事物描述，但错误的统计方法不仅不能反映事实，还会使数据变得毫无意义！

例如在统计公司的工资水准时用平均值常常会迷惑视线，正常用中位数，反映数据集中程度的度量通常有平均数、中位数、众数等，如果这三个是同一个数，则数据是对称分布的，但更多的情况是正倾斜（平均值在后两者左侧）或负倾斜（平均值在后两者右侧）。

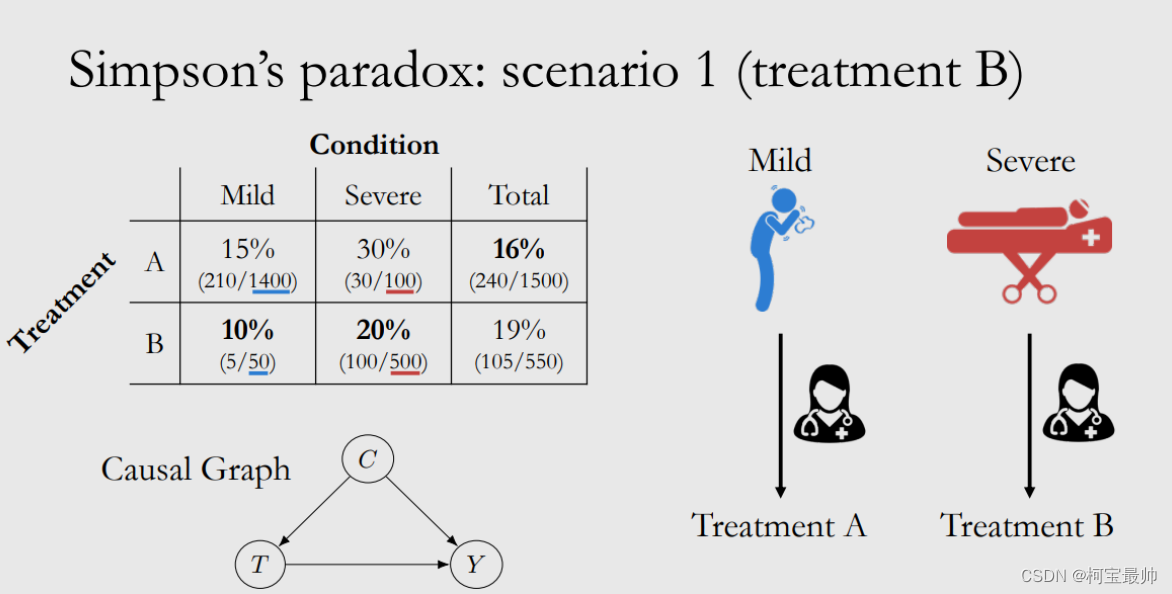
辛普森悖论：如A、B两家医院，总体病人的治愈率A：90%、B：80%，这是你会想着选择A医院，但是如果继续看数据细节把病人分为重症和非重症两类来看，会发现两类分别的治愈率都是B医院较高，B成为了更好选择。这是由于数据中存在潜在变量（如病情严重程度不同病人的占比），按照潜在变量分组后的数据是不均匀的。即在分组比较中占据优势的一方（B医院），在综合评估中却成了失势的一方，该现象成为辛普森悖论。即同一组数据的整体趋势和分组趋势可能完全不同，用数学语言有下列关系式：

当 $\frac{a_1}{b_1}<\frac{c_1}{d_1},\frac{a_2}{b_2}<\frac{c_2}{d_2}$ 时，不能得出 $\frac{a_1+a_2}{b_1+b_2}<\frac{c_1+c_2}{d_1+d_2}$ 的结论，反过来也是不能。

由于此悖论的存在，仅仅通过有限个统计数字无法直接推导和还原真相，这是统计数据的致命缺陷，因为数据可按各种形式分类和比较，潜在变量无穷无尽，不怀好意的人可能会借此给他人呈现处对自己有利的分类拆分数据方法的到的结论。为了避免这种情况，需要仔细分析各种影响因素，不能笼统概括更不能浅尝辄止看待问题！

3、正确解读数据

相关性不等于因果性

两个变量存在相关关系并不代表其中一个变量的改变是由另一个变量引起。相关性体现了两个事物之间相互关联的程度，如房屋面积与价格的正相关性，海拔高度与大气压的负相关性，不过数据之间通常只能呈现关联性，而很难直接体现因果性，AI就是一个典型代表，计算机只能通过发现数据之间的联系而不负责解释原因；而想要得到因果性必须从理论上证明两个变量确实存在因果关系，并且排除所有其他隐含变量同时导致这两个变量的可能性。只通过几组数据不能轻率作结论，很多时候只是表象，无法确认是否存在隐藏在内部的变量！

数据表达的局限性

这个世界是多维的，数据只是其中一维，当我们把现实世界的某件事情或某个状态转变为数据，就已经剔除了（损失了）很多信息，因为数据只表达了事物的一个侧面。如讨论AI时代的就业问题，正方会说出现了越来越多的岗位和职业；反方则说越来越多人因为机器人替代而失去了工作，双方都是正确的但都只能反映该问题的一个方面。

概率就是一种典型的、存在局限的表达。100%肯定的事情与99%可能的事情存在本质区别，以某种药物的99%的治愈率而言，即使只有1%的失败率但是也是威胁人生命的巨大风险。小概率事件必须引起重视，因为概率小不代表风险小。

4、精准预测的挑战

对于生活而言任何一个小的决策、行动、环境改变，都会对未来产生巨大影响；对于一个AI预测模型而言，任何细微的输入变化都会导致截然不同的预测结果，这是一种混沌现象。预测分为两种情况，一种是对客观现象的预测，不受预测本身的影响，如预测地球在宇宙的运行轨迹；另一种指那些会受到预测行为本身影响的预测，如市场、股市、政治，这些会随着预测变动，之前的预测也就失去了意义，这里存在不稳定因素——人的自由意志。