第一章 基础算法（三）—— 双指针，位运算，离散化与区间合并

news2024/10/7 8:20:31

文章目录

    • 双指针
    • 位运算
    • 离散化
    • 区间合并
    • 双指针练习题
      • 799. 最长连续不重复子序列
      • 800. 数组元素的目标和
      • 2816. 判断子序列
    • 位运算练习题
      • 801. 二进制中1的个数
    • 离散化练习题
      • 802. 区间和
    • 区间合并练习题
      • 803. 区间合并

为什么直接用y总的板书？
我是懒狗，不想再画啦

双指针

  • 两个指针分别指向两个不同的序列
  • 两个指针指向同一个序列，快排，表示一段区间

双指针模板：

for (int l = 0, r = 0; r < n; ++r)
{
	while (l < r && check(l, r)) ++r;
	// 每道题的具体逻辑
}

双指针算法的核心思想，运用某些单调性质将N方的朴素算法优化成N
此时每个指针遍历数字的次数不超过n
先思考暴力做法，再思考双重循环中（暴力一般是两个for循环）的单调关系，得到优化做法

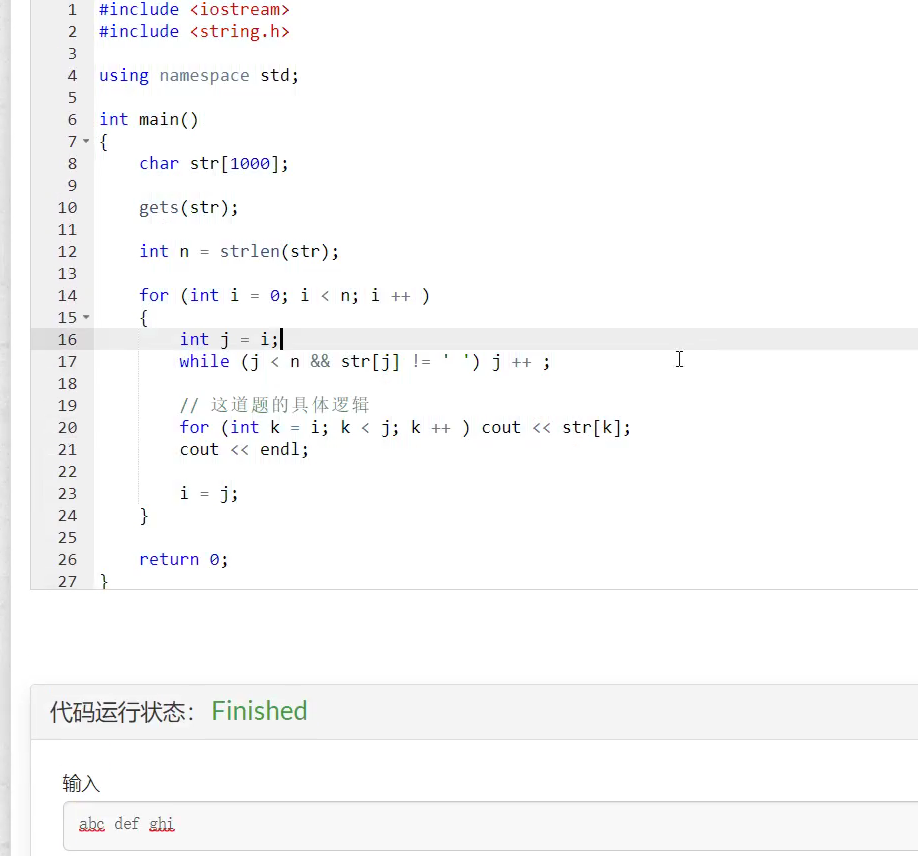
最基本的运用：以空格分隔的单词，以行的形式输出
image.png

位运算

两个运用：

  1. n的二进制表示中第k位是几？
  • 先把第k位移到最后一位
  • 看二进制的个位是几
    结合就是：n >> k & 1，根据题目具体要求，第k位是从0开始还是从1开始？这里涉及一个差一问题，需要根据实际情况考虑一下
  1. lowbit(x)：返回x的最后一位1，具体是lowbit(1010) = 10b，lowbit(10100) = 100b
    具体实现是：x & -x = x & (~x + 1)，注意-x = (~x + 1)
    image.png
    一个具体的运用是：统计x中1出现的次数，对x不断地lowbit，每次减去lowbit得到的数，次数加1。
    直到x为0，说明x中的1被减完了，此时的次数就是x中1出现的次数

模板：

int lowbit(int x) 
{
    return x & (~x + 1);
}

离散化

特指整数离散化
值域比较大，但是数字个数比较少，将这些离散的数映射到连续的区间上的过程，叫做离散化
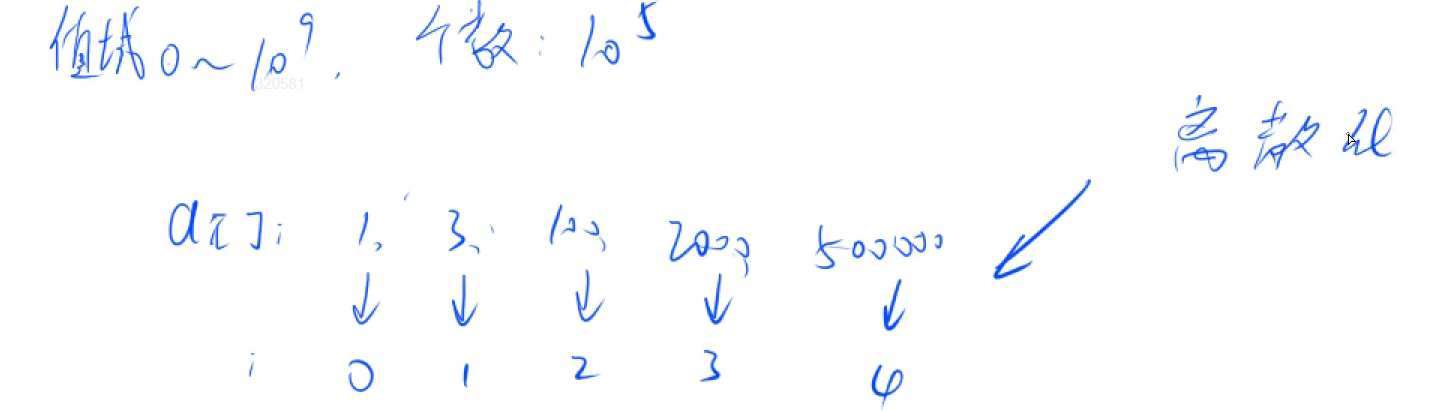
image.png
当数据存储的很分散（位置之间相差很大），比如0, 555，10000, 99999999999，数组中这些位置上的数据都不为0，我要统计某个区间或者整个数组的元素和，怎么办？若遍历所有元素，那么绝大部分的元素遍历是无效的，因为它们的值不会影响结果
对于这些不影响结果的值，我们可以将其忽略。对于影响结果的值，保存它们的位置到一个数组中，此时这些位置与数组下标旧构成了一个唯一的映射关系。将数组下标作为这些位置的新位置，那么原来离散的值就被整合成连续的了
我们可以根据数据原来的位置，在保存离散数据位置的数组中二分，找到该位置的下标，该下标就是原位置的新位置，也就是连续存储的位置
比如数组保存[1, 3, 100, 2000, 500000]这些元素，要找2000的新位置，只要在数组中二分查找2000，得到其下标，即得到其新位置

两个问题：

  1. 数组中可能有重复元素。需要排序并去重
  2. 如何算出 a i a_i ai​离散化后的值？使用二分

排序去重模板：

sort(alls.begin(), alls.end());
erase(unique(alls.begin(), alls.end()), alls.end());

unique：在原数组的基础上，将数组去重，并返回不重合数组的后一个位置
用erase将去重后的重复元素删除，此时的alls中的元素唯一

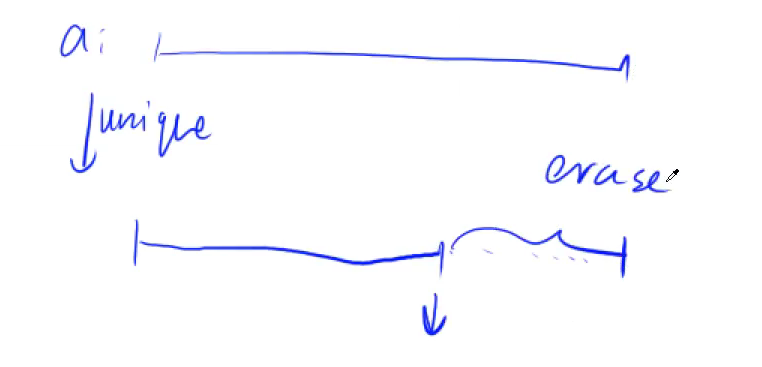
image.png

unique的实现思路：首先，数组不为空时，第一个数肯定能作为不重复的数
其次，因为数组已经排过序，只要一个数与之前的数不一样，那么这个数也能作为不重复的数
当某个数能作为不重复的数时，我们需要保存该数，这里直接在原地保存，即从原数组的开头往后保存这些不重复的数
两个指针：i用来遍历原数组中的所有数，j用来保存不重复的数，即区间[0, j - 1]中的数是不重复的，[j, ed]区间中的数无用

image.png

vector<int>::iterator unique(vector<int>& a)
{
	int j = 0;
	for (int i = 0; i < a.size(); ++ i)
	{
		if (!i || a[i] != a[i - 1]) a[j++] = a[i];
	}
	return a.begin() + j;
}

区间合并

给定多个区间，将有交集的区间合并为一个区间，输出最后区间的数量

  1. 将所有区间按照左端点进行升序排序(C++对pair的排序，先比较first，再比较second)
  2. 选择一个最小的未被遍历过的区间，根据该区间的右端点r，与之后的区间进行比较
  3. 此时会出现两种情况： 两区间有交集，两区间无交集
  • 当两区间有交集时，根据两者较大的r更新当前区间
  • 当两区间无交集时，说明当前区间无法合并了，最终区间的数量+1

双指针练习题

799. 最长连续不重复子序列

799. 最长连续不重复子序列 - AcWing题库
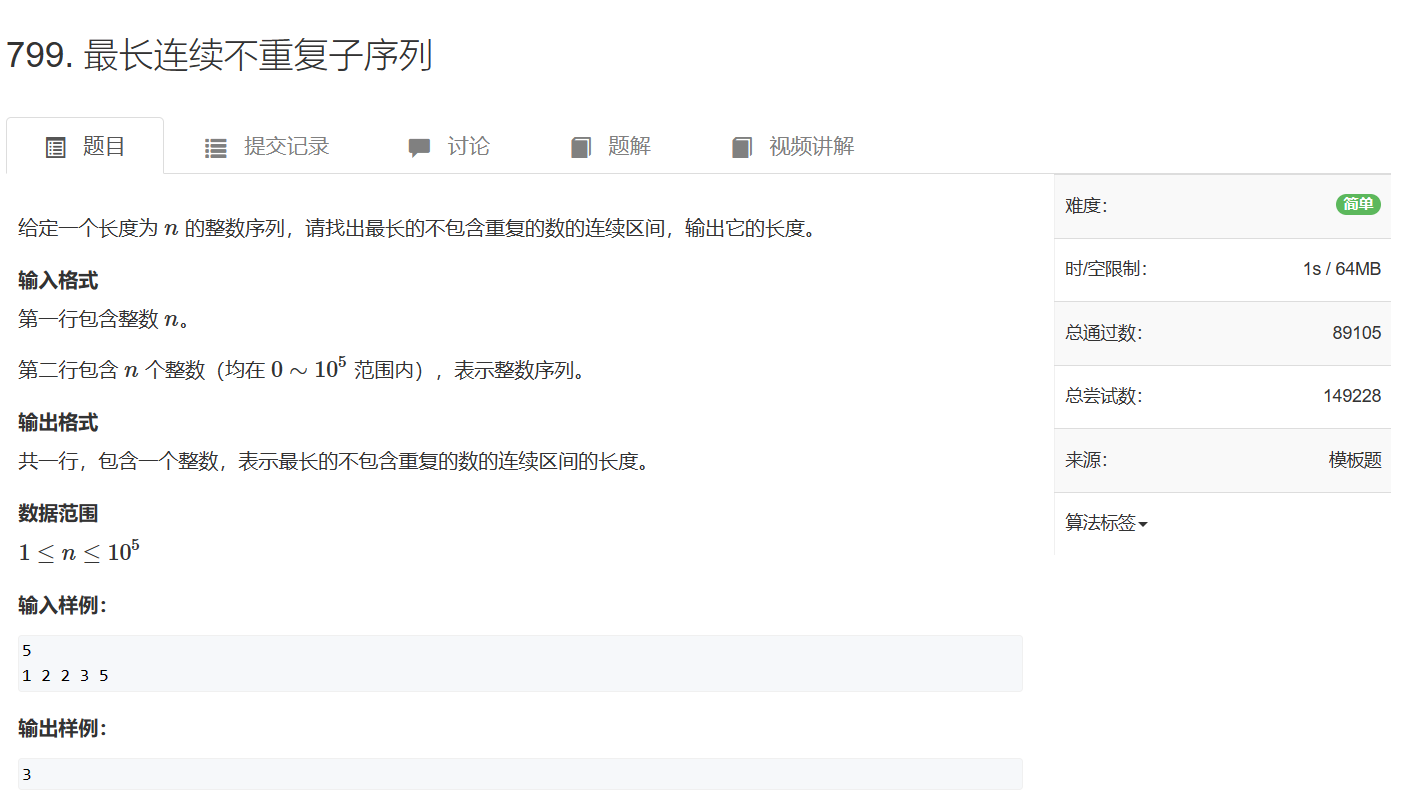
image.png
双指针：l与r
用r遍历序列，每次遍历r时，l尽可能地往左走，使l与r之间的序列在满足字符不重复的情况下，达到最长
这样每次遍历r，就能得到一个[l, r]区间，并且该区间是以r为右端点的最长不重复子序列。因此，每次计算该序列的长度，更新出整个序列中最长不重复子序列

这里要思考每次更新r时，l怎样移动的问题。有点类似dp，在上次的状态更新中，我们已经找出了一个最长子序列[l, r - 1]
此时将更新r - 1为r，由于[l, r - 1]区间中不含重复元素，当r更新时，可以理解为向旧区间添加了一个新字符
若新字符与旧区间中的字符重复，那么l就要向前走，因为只有向前走，才可能剔除区间中字符的字符
直到区间中无重复字符时，l停下，此时的区间[l, r]为以r做为右端点的最长不重复子序列，更新最长的长度即可

若更新 r i r_i ri​为 r i + 1 r_{i+1} ri+1​后，l可以向前走，即将 l i l_i li​更新为 l i − 1 l_{i-1} li−1​，那么就说明区间[ l i − 1 l_{i-1} li−1​, r i + 1 r_{i+1} ri+1​]无重复字符。若区间[ l i − 1 l_{i-1} li−1​, r i + 1 r_{i+1} ri+1​]无重复字符，那么旧区间应该是[ l i − 1 l_{i-1} li−1​, r i r_i ri​]，而不是[ l i l_i li​, r i r_i ri​]，这与我们确定的状态矛盾
也就是说，每次更新r时，得到的区间[l, r]是以r为右端点，往左能构造的最长无重复子序列。也就是说l - 1指向的字符与[l, r]中的某个字符重复

#include <iostream>
using namespace std;

const int N = 1e6 + 10;
int nums[N], S[N];
int n, res = 1;

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) scanf("%d", &nums[i]);
    
    for (int l = 0, r = 0; r < n; ++r)
    {
        S[nums[r]]++;
        while (S[nums[r]] > 1) S[nums[l]]--, ++l;
        res = max(res, r - l + 1);
    }
    
    printf("%d", res);
    return 0;
}

800. 数组元素的目标和

800. 数组元素的目标和 - AcWing题库
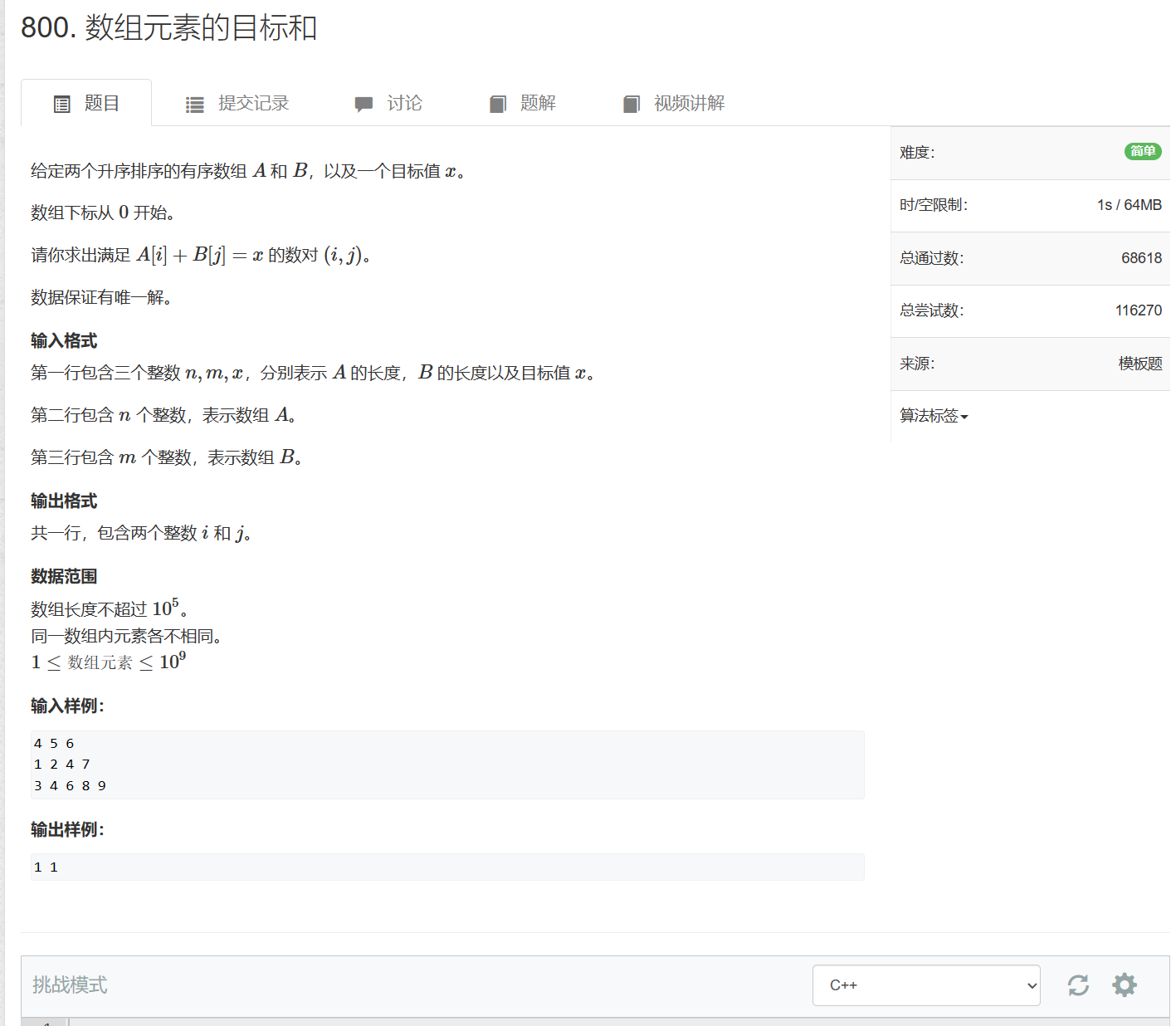
image.png

利用有序数列的单调性，假设现在有两个数组 a n a_n an​与 b n b_n bn​，分别用i和j两个指针遍历，j指针从头开始遍历，i指针从尾开始遍历
用二分找到第一个 a i a_i ai​ + b j b_j bj​ <= x的 a i a_i ai​，之后再判断 a i a_i ai​ + b j b_j bj​ == x
此时 a n a_n an​搜索区间就缩小成了[0, i]，因为 b j b_j bj​ + a i a_i ai​中， a i a_i ai​是第一个小于等于x的数。 b j b_j bj​ + a i + 1 a_{i+1} ai+1​ 必定大于x
b j + 1 b_{j+1} bj+1​ + a i + 1 a_{i+1} ai+1​ 也必定大于x，所以 b j + 1 b_{j+1} bj+1​ + a i a_i ai​ 才可能小于等于x，此时从 a 0 a_0 a0​ ~ a i a_i ai​之间中，找到第一个满足 a k a_k ak​ + b j + 1 b_{j+1} bj+1​ <= x的 a k a_k ak​

#include <iostream>
#include <vector>

using namespace std;

typedef long long ll;

const int N = 1e6 + 10;
int n, m;
ll x;
int a[N], b[N];

int find(int l, int r, int b)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (b + a[mid] <= x) l = mid;
        else r = mid - 1;
    }
    return l;
}

int main()
{
    scanf("%d%d%lld", &n, &m, &x);
    for (int i = 0; i < n; ++i) scanf("%d", &a[i]);
    for (int i = 0; i < m; ++i) scanf("%d", &b[i]);
    
    for (int i = n - 1, j = 0; j < m; ++j)
    {
        // 更新i
        i = find(0, i, b[j]);
        if (0LL + a[i] + b[j] == x) 
        {
            printf("%d %d\n", i, j);
            break;    
        }
    }
    return 0;
}

2816. 判断子序列

2816. 判断子序列 - AcWing题库
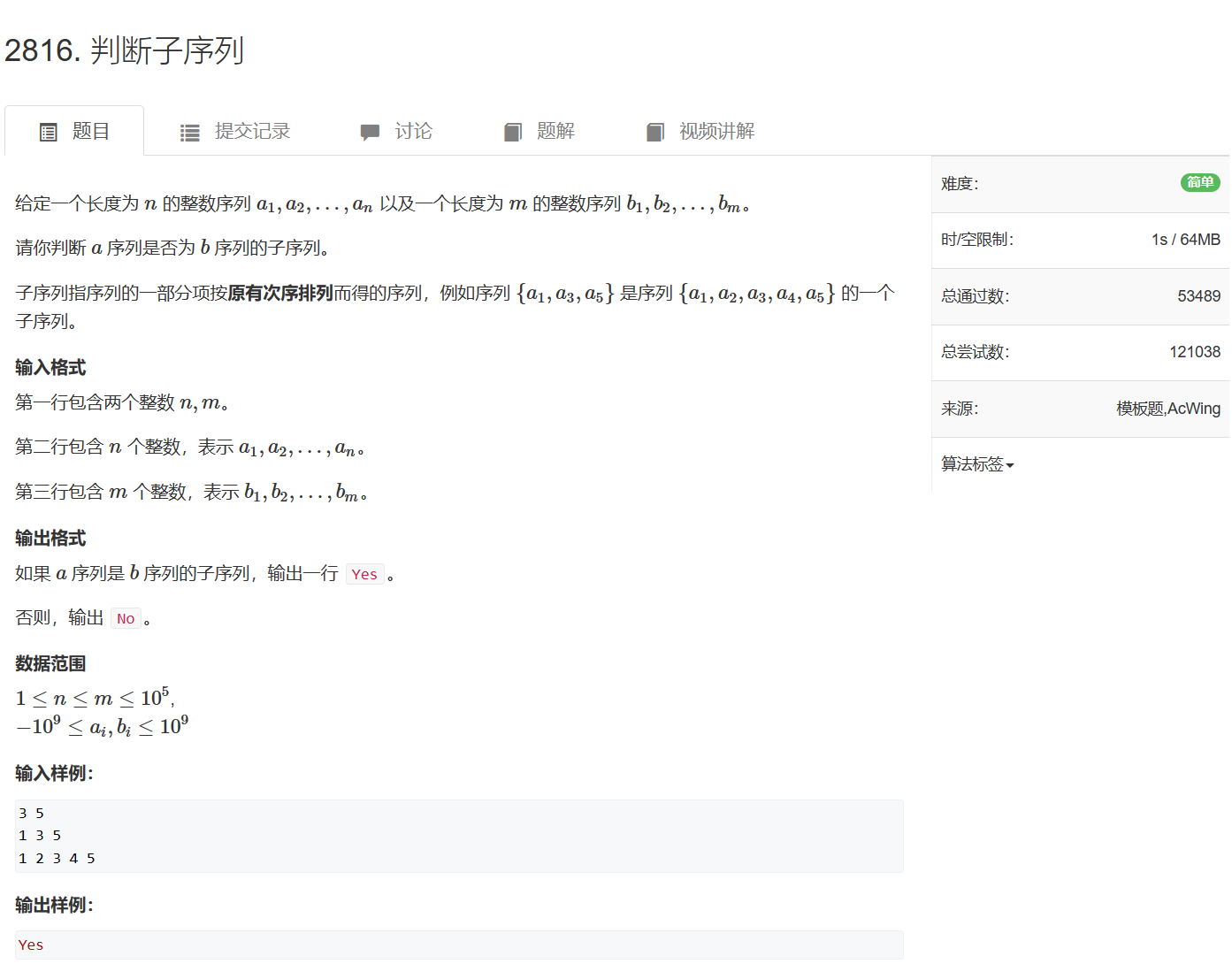
image.png

这个实在想不到怎么用暴力解，双指针一下就看出来了。不像上一题，只能想到暴力，然后再根据单调性，用双指针优化
两个指针i和j分别指向两个数组的开头，j不断移动，当a[i] == b[j]时，i移动，当i遍历完数组，输出Yes

#include <iostream>
using namespace std;

const int N = 1e6 + 10;
int n, m;
int i, j;
int a[N], b[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (i = 0; i < n; ++i) scanf("%d", &a[i]);
    for (i = 0; i < m; ++i) scanf("%d", &b[i]);
    
    for (i = 0, j = 0; i < n && j < m; ++j)
    {
        while (i < n && j < m && a[i] == b[j]) i++, j++;
    }
    
    if (i == n) printf("Yes\n");
    else printf("No\n");
    
    return 0;
}

while (i < n && j < m && a[i] == b[j]) i++, j++;
没有注意细节：之前判断条件i < n && j < m没写
a[i] == b[j]写成了a[i+] == b[j++]
WA了两次

不要被模板限制，这题可以直接用while写

#include <iostream>
using namespace std;

const int N = 1e6 + 10;
int n, m;
int a[N], b[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; ++i) scanf("%d", &a[i]);
    for (int i = 0; i < m; ++i) scanf("%d", &b[i]);
    
    int i = 0, j = 0;
    while (i < n && j < m)
    {
        if (a[i] == b[j]) i++;
        j++;
    }
    
    if (i == n) printf("Yes\n");
    else printf("No\n");
    
    return 0;
}

位运算练习题

801. 二进制中1的个数

801. 二进制中1的个数 - AcWing题库
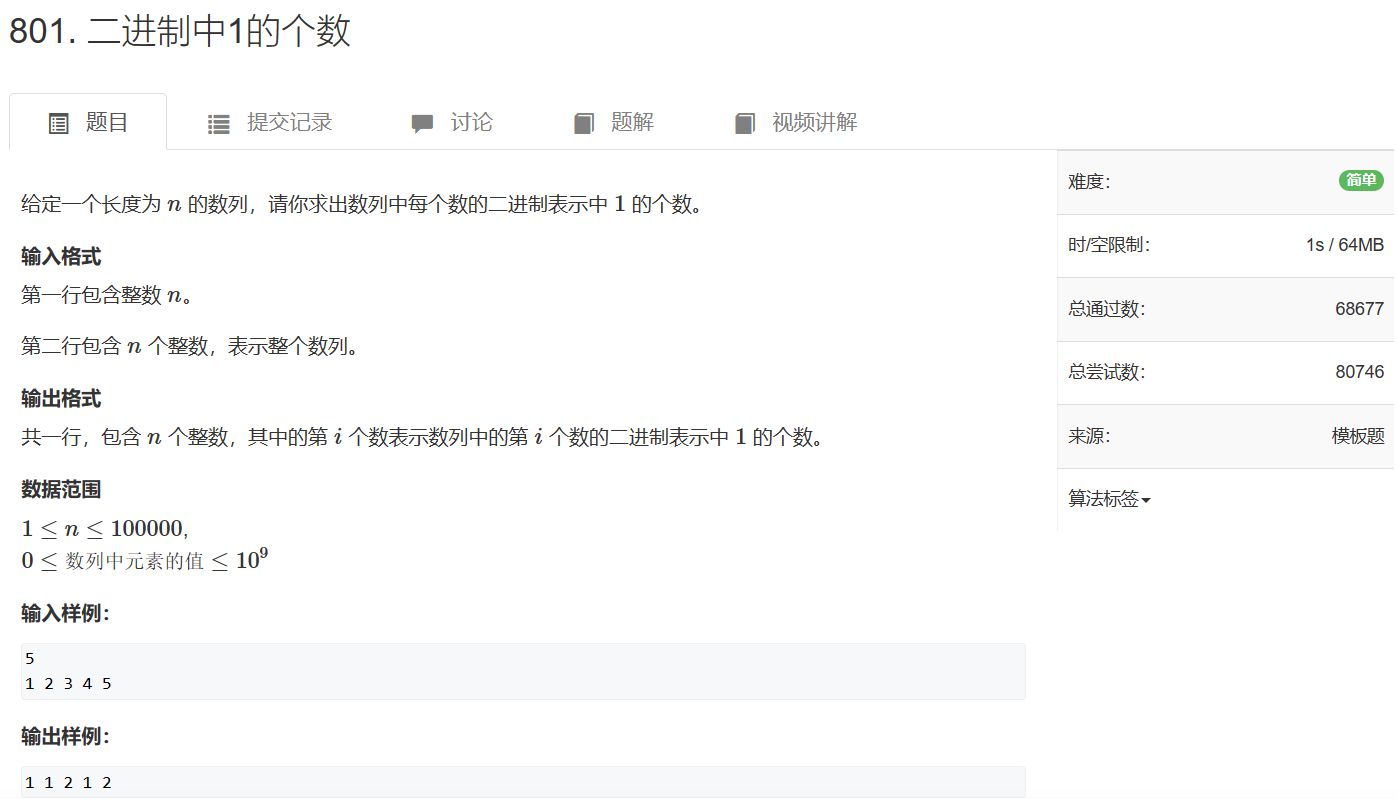
image.png

lowbit的使用，减去n次lowbit，n即为答案

#include <iostream>
using namespace std;

int n, x;

int lowbit(int x) 
{
    return x & (~x + 1);
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) 
    {
        scanf("%d", &x);
        int res = 0;
        while (x)
        {
            x -= lowbit(x);
            res++;
        }
        printf("%d ", res);
    }
    
    return 0;
}

离散化练习题

802. 区间和

802. 区间和 - AcWing题库
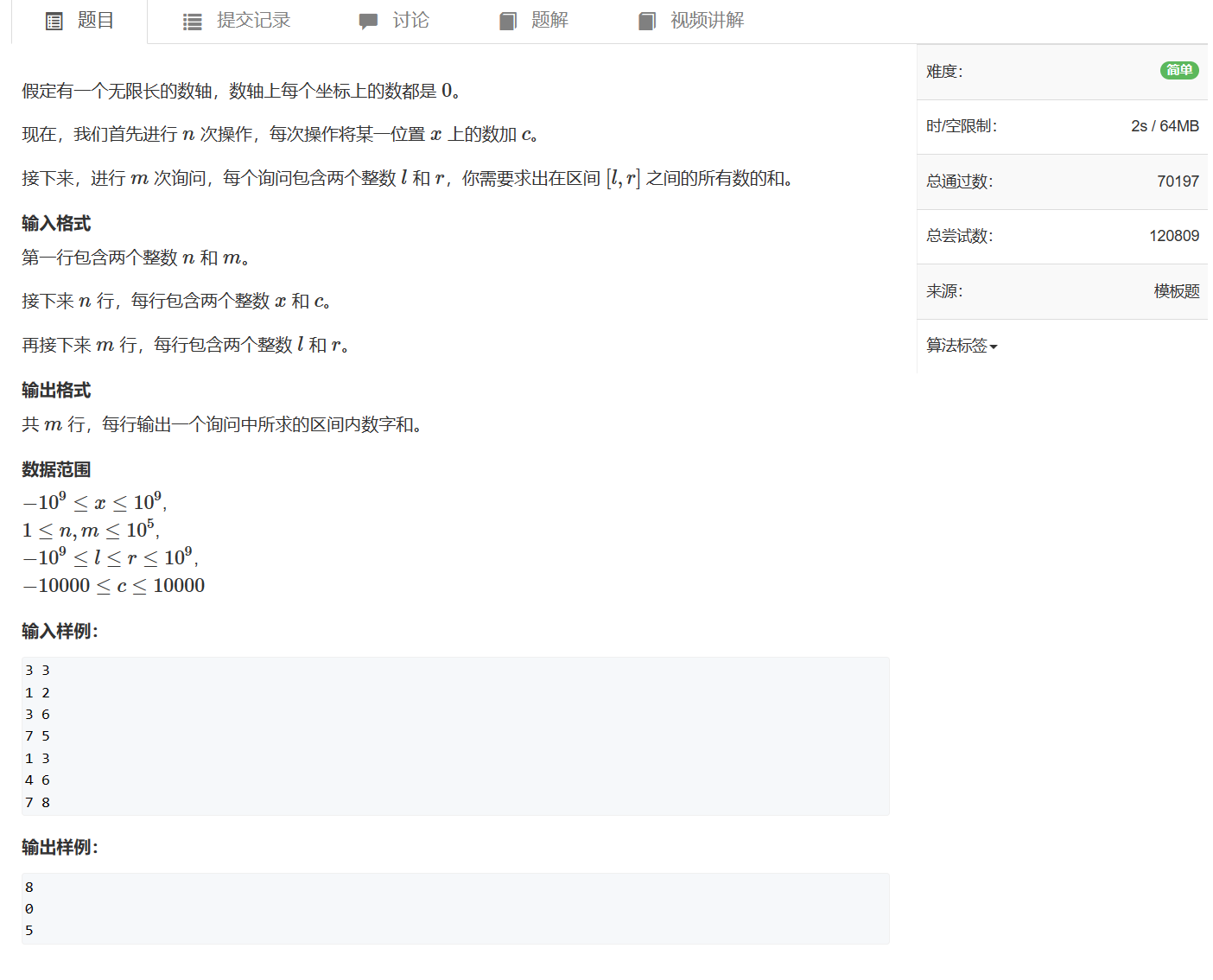
image.png

题目有两个操作，一是将某个位置的数加上特定值，二是询问某个区间中的值总和
求区间的值总和，使用前缀和数组完成
现在的问题是，这些值过于分散，前缀和数组以及保存这些值的数组将浪费大量空间
所以需要进行预处理，使这些离散的值连续，用数组将值的位置保存，将这些离散的位置用数组下标重新映射，使之成为连续的位置
这样处理后，离散的值变得连续
所以我们需要知道题目会用到哪些离散的位置，首先是保存值的位置，其次是询问区间的端点
考虑最坏情况，将这些位置用alls数组保存起来，并用数组下标进行重新映射
当要找某个位置时，根据alls位置保存的值（位置），获取其映射后的位置（所在的数组下标）

所以alls数组用来将离散位置进行连续化，重新构建索引后的位置为数组的下标
至于这些位置上的值，另外使用其他数组进行保存

用pair保存题目的两个操作，分别是对某个位置加上某个值，以及询问某个区间的值
对离散的位置进行重新索引后，这两个操作都要转换成对新索引的操作

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

const int N = 3e6 + 10;
vector<PII> add, query;
vector<int> alls;
int a[N];

int n, m;
int x, c, l, r;

int find(int x)
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return l + 1;
}

int main()
{
    scanf("%d%d", &n, &m);
    // 保存离散的位置，以及这些位置要加上的值
    for (int i = 0; i < n; ++ i) 
    {
        cin >> x >> c;
        add.push_back({x, c});
        alls.push_back(x);
    }
    // 保存这些区间的位置，以及询问的区间
    for (int i = 0 ; i < m; ++ i)
    {
        cin >> l >> r;
        query.push_back({l, r});
        alls.push_back(l), alls.push_back(r);
    }
    
    // 对alls进行排序去重
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());
    
    // 二分查找新索引，增加位置上的值
    for (auto item : add) a[find(item.first)] += item.second;
    
    // 构建前缀和数组
    for (int i = 1; i <= alls.size(); ++ i) a[i] += a[i - 1];
    
    // 根据查询区间返回区间和
    for (auto item : query) 
    {
        l = find(item.first), r = find(item.second);
        printf("%d\n", a[r] - a[l - 1]);
    }
    
    return 0;
}

区间合并练习题

803. 区间合并

803. 区间合并 - AcWing题库
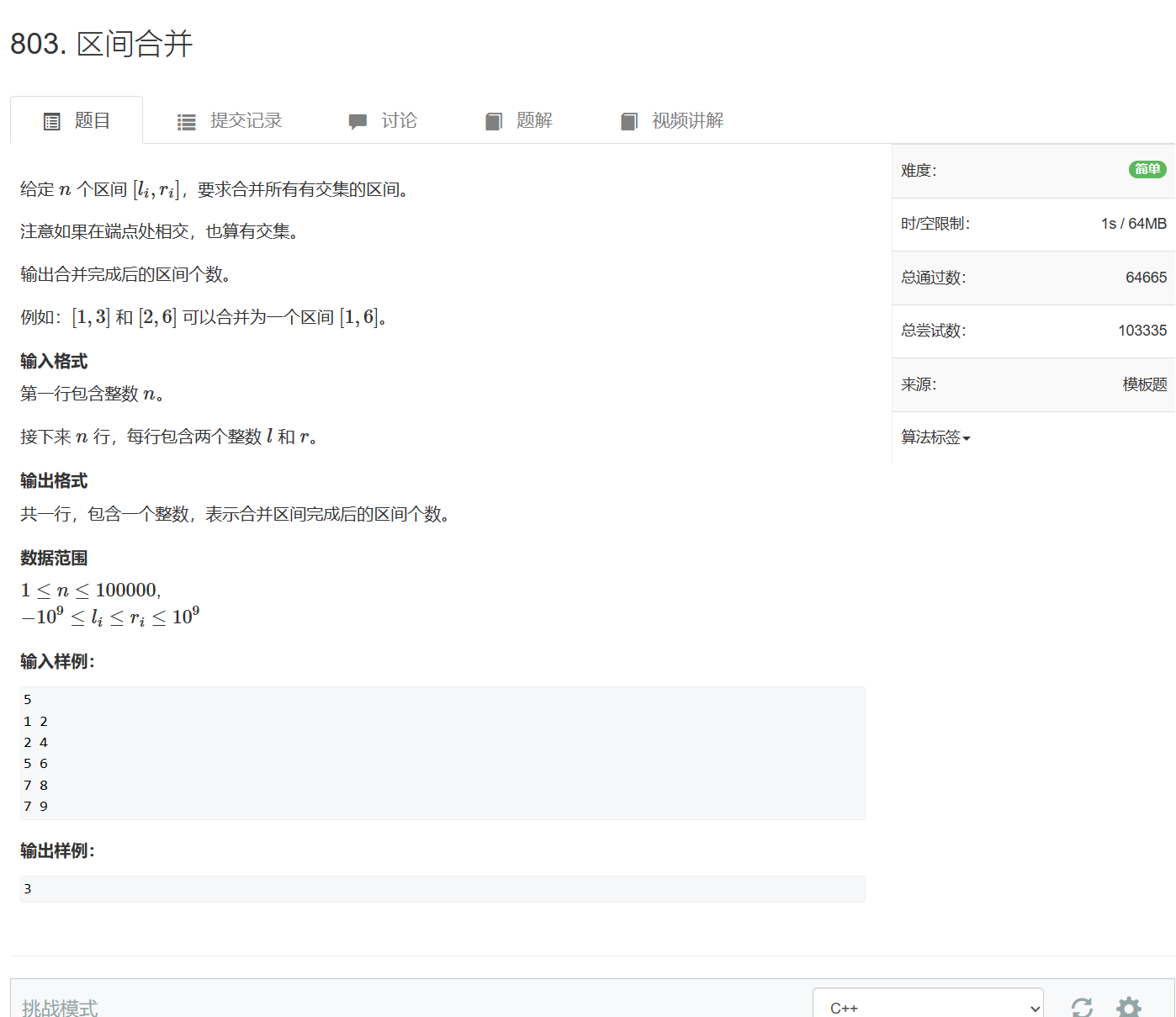
image.png

将区间按照左端点优先，其次右端点的优先级进行排序（使用STL的sort）。维护一个当前区间并根据后续区间更新当前区间

当前区间与后续区间无交集时，说明区间无法合并，此时最终区间的数量+1
否则更新区间

需要注意的是：设置起始区间为一个题目不可能给定的区间，然后再进行更新

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

int n, res;
int l, r, st = -2e9, ed = -2e9;
vector<PII> segs;

int main()
{
    scanf("%d", &n);
    for (int i = 0 ; i < n; ++ i) 
    {
        scanf("%d%d", &l, &r);
        segs.push_back({l, r});
    }
    
    sort(segs.begin(), segs.end());
    for (auto seg : segs)
    {
        // 判断区间是否重合
        if (seg.first <= ed) ed = max(ed, seg.second);
        else 
        {
            if (st != -2e9) ++res;   
            st = seg.first, ed = seg.second;
        }
    }
    if (st != -2e9) ++res;
    
    printf("%d\n", res);
    return 0;
}

还是有一些细节需要注意的：选择的初始区间与后续区间无交集时，最终的区间数量不能+1
最后将最终的区间数量+1，因为最后一个区间无后续区间，此时该区间可以作为一个无法合并的区间
当然，题目规定了区间数量大于0，所以这题可以不用考虑给定区间为空的情况。使用排序后的第一个区间作为起始区间，省去判断

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

int n, res;
int l, r;
vector<PII> segs;

int main()
{
    scanf("%d", &n);
    for (int i = 0 ; i < n; ++ i) 
    {
        scanf("%d%d", &l, &r);
        segs.push_back({l, r});
    }
    
    sort(segs.begin(), segs.end());
    
    int st = segs[0].first, ed = segs[0].second;
    
    for (int i = 1; i < segs.size(); ++i)
    {
        // 判断区间是否重合
        if (segs[i].first <= ed) ed = max(ed, segs[i].second);
        else st = segs[i].first, ed = segs[i].second, res++;
    }
    
    printf("%d\n", res + 1);
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/669539.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

音乐考级系统python+mysql

音乐考级系统python+mysql

目录 废话不多说下面看严谨版不带web界面的&#xff1a; 总结&#xff1a; 写这个博客呢主要是因为之前学校有个简单的课设要做&#xff0c;想着白嫖一个交差的&#xff0c;但是找了一圈没找到合适的能拿来用的&#xff0c;我就下班用了两晚手搓了一个代码。 具体的建表语句…
阅读更多...
PCB设计实验｜第二周｜谐波振荡电路实验｜3月6日

PCB设计实验｜第二周｜谐波振荡电路实验｜3月6日

目录 实验二 谐波振荡电路实验 一、实验原理 二、实验环境 三、实验结果及分析 四、实验总结 实验二 谐波振荡电路实验 一、实验原理 利用深度正反馈&#xff0c;通过阻容耦合使两个电子器件交替导通与截止&#xff0c;从而自激产生方波输出的振荡器&#xff0c;常用作…
阅读更多...
ChatGPT在前，华为盘古Chat在后

ChatGPT在前，华为盘古Chat在后

国产盘古Chat对话方面堪比GPT-3.5 什么是ChatGPT&#xff1f;简单来说&#xff0c;就是一个能够和人类自然对话的人工智能系统。它可以理解你的语言&#xff0c;回答你的问题&#xff0c;甚至给你提供建议和服务。它不仅可以处理文字&#xff0c;还可以处理图片、视频、音频等…
阅读更多...
基于Java学生信息管理系统-控制台版

基于Java学生信息管理系统-控制台版

基于Java学生信息管理系统-控制台版 一、系统介绍二、功能展示1.学生信息添加2.学生信息修改3.学生信息查询4.学生信息删除5.退出系统 三、代码展示四、其它1.其他系统实现2.获取源码 一、系统介绍 学生信息的添加、修改、删除、查询、退出系统 二、功能展示 1.学生信息添加…
阅读更多...
【面试题01】抽象类、接口 的区别和使用场景

【面试题01】抽象类、接口 的区别和使用场景

文章目录 一、抽象类和接口的区别1.1 定义方式不同1.2.成员方法不同1.3 实现方式不同1.4 构造方法不同1.5 访问修饰符不同1.6 关注点不同 二、抽象类和接口的使用场景2.1 抽象类的使用场景2.2 接口的使用场景 三、PHP代码演示总结 一、抽象类和接口的区别 抽象类和接口基本上是…
阅读更多...
提升效率，使用ChatGPT的轻松撰写日报和周报

提升效率，使用ChatGPT的轻松撰写日报和周报

日报和周报是办公生活中不可或缺的部分&#xff0c;它们有助于记录工作进展、分享关键信息和与团队保持沟通。但是&#xff0c;有时写作这些报告可能会变得繁琐和耗时。在本文中&#xff0c;我们将介绍如何利用ChatGPT&#xff0c;一个强大的自然语言处理模型&#xff0c;提高写…
阅读更多...
安卓开发级联显示菜单-省市区显示举例

安卓开发级联显示菜单-省市区显示举例

安卓开发级联显示菜单-省市区显示举例 问题背景 安卓日常开发过程&#xff0c;经常会有需要级联显示的场景&#xff0c;比如省市区显示等&#xff0c;或者各种组织结构级联显示&#xff0c;本文将介绍安卓开发过程实现级联显示的一种方案。 实现效果如下&#xff1a; 问题分…
阅读更多...
GaussDB整体性能慢分析

GaussDB整体性能慢分析

目录 问题描述问题现象告警业务影响原因分析分析步骤分析定位方法步骤一步骤二步骤三步骤四CPU满I/O满或者I/O异常内存满网络异常 步骤五并发问题数据库配置问题异常等待事件长时间性能下降短时性能抖动不优SQL 问题描述 整体性能慢。不满足客户作业对时延要求或者不满足客户预…
阅读更多...
微信小程序 u-picker 三级联动 uView

微信小程序 u-picker 三级联动 uView

微信小程序 u-picker 三级联动 uView 场景 移动端微信小程序框架 uView 中的 u-picker 实现三级联动 数据是一级一级加载的 [12,1201,120101] 多列联动 先了解属性参数 mode可以设置为&#xff1a;time、region、selector、multiSelector&#xff0c;区分时间、地区、单列&am…
阅读更多...
2022高教社杯全国大学生数学建模竞赛B题解析（更新完结）

2022高教社杯全国大学生数学建模竞赛B题解析（更新完结）

2022高教社杯全国大学生数学建模竞赛B题解析&#xff08;更新完结&#xff09; 题目解析前言问题一1.11.21.3问题二 题目 B 题 无人机遂行编队飞行中的纯方位无源定位 无人机集群在遂行编队飞行时&#xff0c;为避免外界干扰&#xff0c;应尽可能保持电磁静默&#xff0c;少向…
阅读更多...
LC-LCP 41. 黑白翻转棋

LC-LCP 41. 黑白翻转棋

LCP 41. 黑白翻转棋 难度中等32 在 n*m 大小的棋盘中&#xff0c;有黑白两种棋子&#xff0c;黑棋记作字母 "X", 白棋记作字母 "O"&#xff0c;空余位置记作 "."。当落下的棋子与其他相同颜色的棋子在行、列或对角线完全包围&#xff08;中间不…
阅读更多...
Kotlin 一劳永逸实现 TAG

Kotlin 一劳永逸实现 TAG

1 TAG 经典写法 对于 Android 开发&#xff0c;当我们需要在类中打印 Log 时&#xff0c;通常在Java中会这么定义一个 TAG&#xff1a; private static final String TAG "TestClass"; 或者不具体指定名字&#xff1a; private static final String TAG TestClass.…
阅读更多...
Java粮油质量管控防伪溯源系统源码 粮油MES源码

Java粮油质量管控防伪溯源系统源码 粮油MES源码

Java粮油质量管控防伪溯源系统源码&#xff0c; 粮油MES源码&#xff0c;有演示&#xff0c;有源码。 一、全生命周期的追踪与溯源 &#xff08;1&#xff09;通过一物一码管理生产销售、追踪包装关联&#xff0c;配送管理及终端查询来实现窜货预警&#xff0c;及时处理问题&…
阅读更多...
（一）rstudio容器用户配置root权限，安装conda

（一）rstudio容器用户配置root权限，安装conda

1、查看运行中的容器&#xff1a;docker ps 2、进入容器&#xff1a;docker exec -it my_rstudio /bin/bash 3、安装工具&#xff1a;apt-get install 4、查看权限配置文件&#xff1a;cat /etc/sudo 5、查看确认用户(rstudio)&#xff1a;cat /etc/passwd | cut -d: -f1 ro…
阅读更多...
判断给定数据中是否存在True只要存在一个True结果为Turenp.sometrue()

判断给定数据中是否存在True只要存在一个True结果为Turenp.sometrue()

【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 判断给定数据中是否存在True 只要存在一个True结果为Ture np.sometrue() 选择题 下列说法错误的是? import numpy as np a np.array([False, False, True]) print("【显示】a "…
阅读更多...
三年时间打磨，MeterSphere v2.10 LTS版本给测试用户带来的价值

三年时间打磨，MeterSphere v2.10 LTS版本给测试用户带来的价值

2023年5月&#xff0c;MeterSphere开源持续测试平台&#xff08;https://github.com/metersphere&#xff09;发布了v2.10 LTS版本。这是这个开源项目自2020年2月写下第一行代码后发布的第三个LTS版本。 在软件行业&#xff0c;LTS&#xff08;即Long Term Support&#xff09…
阅读更多...
SQL太慢如何进行优化

SQL太慢如何进行优化

1.慢SQL优化思路。 慢查询日志记录慢SQL explain分析SQL的执行计划 profile 分析执行耗时 Optimizer Trace分析详情 确定问题并采用相应的措施 1.1 慢查询日志记录慢SQL 如何定位慢SQL呢、我们可以通过慢查询日志来查看慢SQL。默认的情况下呢&#xff0c;MySQL数据库是不开…
阅读更多...
C盘文件恢复怎么做？数据恢复，就看这4招！

C盘文件恢复怎么做？数据恢复，就看这4招！

我一般比较重要的文件都会保存到c盘中。最近电脑有点卡顿&#xff0c;想清理一下不需要的文件&#xff0c;但不小心删除了一个很重要的文件&#xff0c;c盘删除的文件还能恢复吗&#xff1f;谁可以帮我想想c盘中的文件如何恢复呢&#xff1f; C盘对于电脑来说是个很重要的磁盘&…
阅读更多...
Linux教程——Vim移动光标快捷键汇总

Linux教程——Vim移动光标快捷键汇总

Vim 文本编辑器中&#xff0c;最简单的移动光标的方式是使用方向键&#xff0c;但这种方式的效率太低&#xff0c;更高效的方式使用快捷键。 Vim 移动光标常用的快捷键及其功能如下面各表所示&#xff0c;需要注意的是&#xff0c;表中所有的快捷键都在命令模式&#xff08;默…
阅读更多...
安卓蓝牙L2CAP协议简介及报文格式

安卓蓝牙L2CAP协议简介及报文格式

概述 逻辑链路控制和适配协议&#xff08;Logical Link Control and Adaptation Protocol&#xff0c;L2CAP&#xff09;是蓝牙的核心协议&#xff0c;负责适配基带中的上层协议。它同链路管理器并行工作&#xff0c;向上层协议提供定向连接的和无连接的数据业务。L2CAP具有分…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023