题目

B 题 无人机遂行编队飞行中的纯方位无源定位
无人机集群在遂行编队飞行时，为避免外界干扰，应尽可能保持电磁静默，少向外发射电磁波信号。为保持编队队形，拟采用纯方位无源定位的方法调整无人机的位置，即由编队中某几架无人机发射信号、其余无人机被动接收信号，从中提取出方向信息进行定位，来调整无人机的位置。编队中每架无人机均有固定编号，且在编队中与其他无人机的相对位置关系保持不变。接收信号的无人机所接收到的方向信息约定为：该无人机与任意两架发射信号无人机连线之间的夹角（如图 1 所示）。例如：编号为 FY01、FY02 及 FY03 的无人机发射信号，编号为FY04 的无人机接收到的方向信息是 𝛼1，𝛼2 和 𝛼3。 图 1 无人机接收到的方向信息示意图

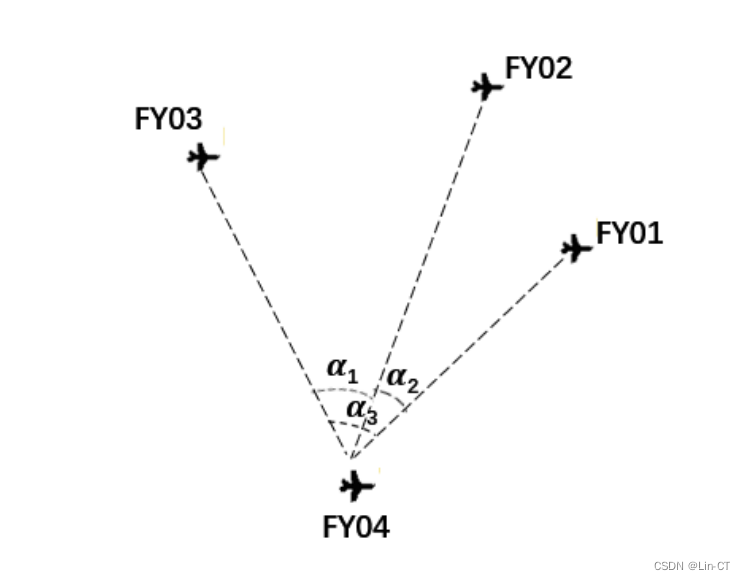
请建立数学模型，解决以下问题：
问题 1 编队由 10 架无人机组成，形成圆形编队，其中 9 架无人机（编号 FY01~FY09）均匀分布在某一圆周上，另 1 架无人机（编号 FY00）位于圆心（见图 2）。无人机基于自身感知的高度信息，均保持在同一个高度上飞行。

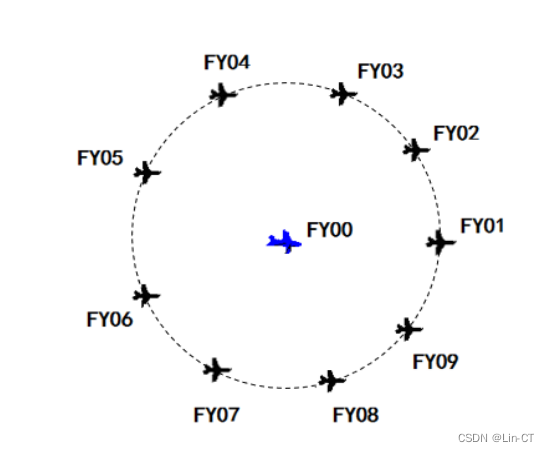
图 2 圆形无人机编队示意图
(1) 位于圆心的无人机（FY00）和编队中另 2 架无人机发射信号，其余位置略有偏差的无人机被动接收信号。当发射信号的无人机位置无偏差且编号已知时，建立被动接收信号无人机的定位模型。
(2) 某位置略有偏差的无人机接收到编号为 FY00 和 FY01 的无人机发射的信号，另接收到编队中若干编号未知的无人机发射的信号。若发射信号的无人机位置无偏差，除 FY00 和 FY01外，还需要几架无人机发射信号，才能实现无人机的有效定位？
(3) 按编队要求，1 架无人机位于圆心，另 9 架无人机均匀分布在半径为 100 m 的圆周上。当初始时刻无人机的位置略有偏差时，请给出合理的无人机位置调整方案，即通过多次调整，每次选择编号为 FY00 的无人机和圆周上最多 3 架无人机遂行发射信号，其余无人机根据接收
到的方向信息，调整到理想位置（每次调整的时间忽略不计），使得 9 架无人机最终均匀分布在某个圆周上。利用表 1 给出的数据，仅根据接收到的方向信息来调整无人机的位置，请给出具体的调整方案。

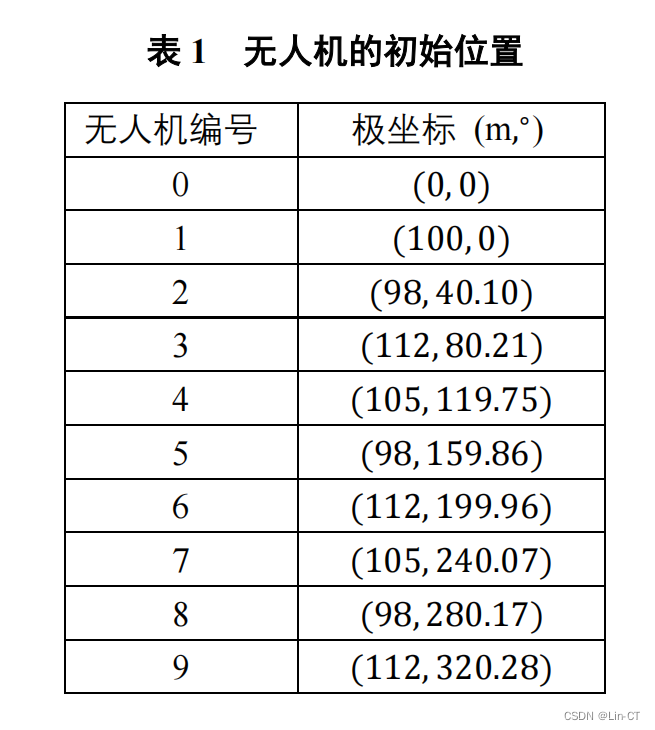
表 1 无人机的初始位置
无人机编号 极坐标 (m,∘) 0 (0, 0) 1 (100, 0) 2 (98, 40.10) 3 (112, 80.21) 4 (105, 119.75) 5 (98, 159.86) 6 (112, 199.96) 7 (105, 240.07) 8 (98, 280.17) 9 (112, 320.28)
问题 2 实际飞行中，无人机集群也可以是其他编队队形，例如锥形编队队形（见图 3，直线上相邻两架无人机的间距相等，如 50 m）。仍考虑纯方位无源定位的情形，设计无人机位置调整方案。

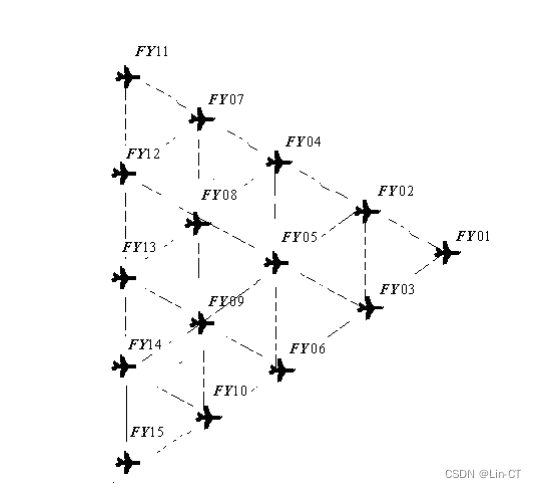
图 3 锥形无人机编队示意图

解析

前言

数学建模主要是让大家构建自己的模型，只要能解决问题的模型就是好模型，无标准答案。我个人的分析过程大致如下文，仅个人观点不一定是正确的，不说太多怕限制了大家的思维哈哈哈。

问题一

1.1

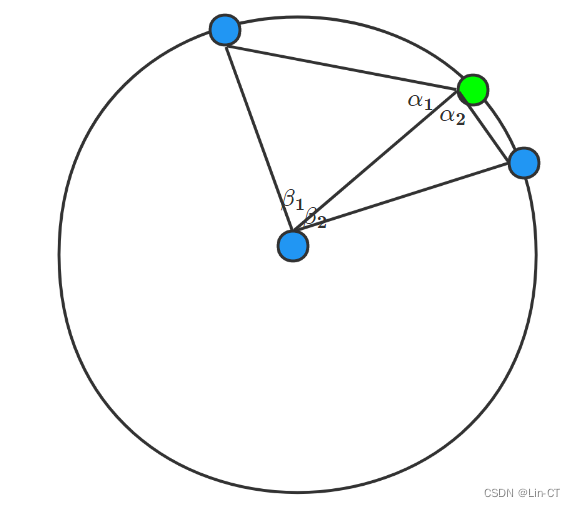
由于发送信号的无人机位置无偏差且编号已知，又个无人机按编号顺序排列，因此可以根据编号差结合三角函数关系构建模型。

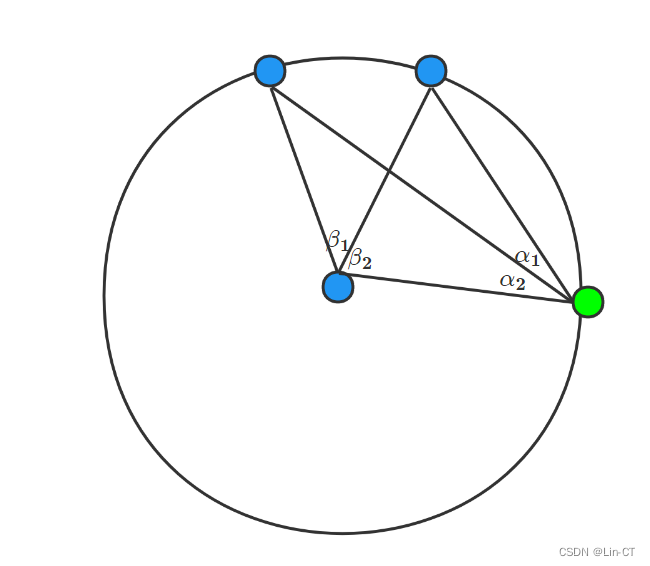
如上图，蓝色为已知飞机，绿色未知。根据两个蓝色编号差就可以求出β1的大小，在圆中根据三角函数关系用α1与2表达出β2，将该β2与根据编号差所计算得到β2作差或做商得到一个影响因子，根据它就可以调整无人机位置，实现定位。
当然还会有多种无人机分布情况，是否用分段函数等具体情况就大家自己看情况了。

1.2

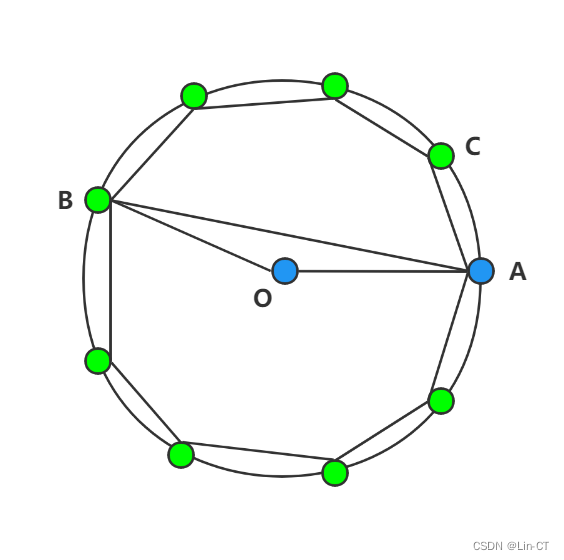
因为9驾飞机均匀分布因此可以初始化各个编号飞机的α角即角ABO的大小，运动过程中比较初始角与信号角的大小即可判断位置是否偏移，但是若只有OA两架飞机仍无法确定B需要朝那个方位移动调整角度，因此必须要更多的信号角度信息。

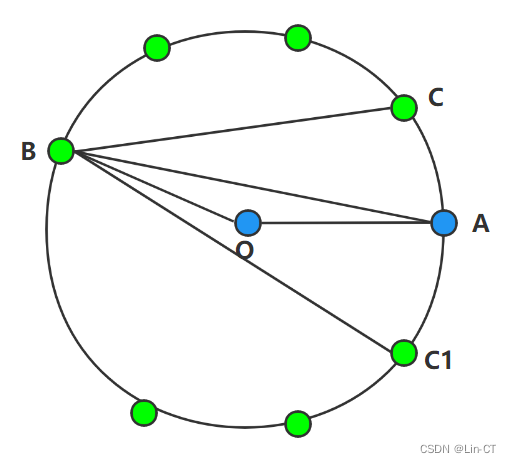
假设在多一个未确定飞机C的信号，根据角度信息可能会有C和C1两种情况，如下图所示，当在C位置时角OBC必大于角ABC，在C1位置时角OBC1必小于角ABC1，因此根据信号的角度信息可以确定C与B是同侧或异侧，题目给出只是略微偏移，而发信息飞机位置准确，因此根据信号角度与初始时的角度对比就可以知道发信号的C的编号，进而再对比OBA、OBC、ABC三个角的当前与初始角度，分析前后偏移与左右偏移从而推算B该朝何方位飞行。是否多加这一台就可以确定飞机如何调整定位大家自己验证，这是竞赛！！！

1.3

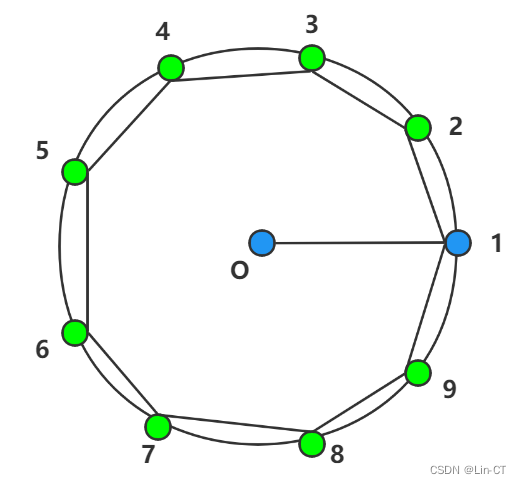
在初始位置有偏差的情况下，因为半径为100因此可以固定0和1的机位，其他飞机调整位置，0和1的信号必须接收，首先计算以0和1为基准的正九边形各点相对于01飞机的α角。注意这里题目要求的是给出具体方案，因此可以直接安排几号机给几号机发信号。这里有两种方案，一种用计算机思维利用类似粒子群算法进行整体调整；另一种就是利用正九边形下的α角与当前α的关系直接调。说说第二种方案，可以由近到远调，捆绑对称点，在选一个远点，例如对2就选对称点9以及同侧的最远点5进行调整。由于题目要求具体方案，因此最终方案一定要讲清楚调整规则及流程或是调整函数的构建，最好能具体化多次调整的相对角度大小。

问题二

这么多人看有亿点点压力，在重复一遍前言，数学建模主要是让大家构建自己的模型，只要能解决问题的模型就是好模型，无标准答案。这仅是我个人观点不一定是正确的，不说太多怕限制了大家的思维哈哈哈。
对于问题二，首先发射信号的无人机并不是固定的那几辆，要多次切换使得整体形成队形准确。可以直接卡死一号机的位置，让他作为整个队形的标准，始终发射信号。首先先边角三辆发射信号，其他飞机接收，其中每个飞机根据接收到的三个α角与标准等边三角形的α角的关系进行调整，调整都形成大致轮廓，但不一定就是标准队形。

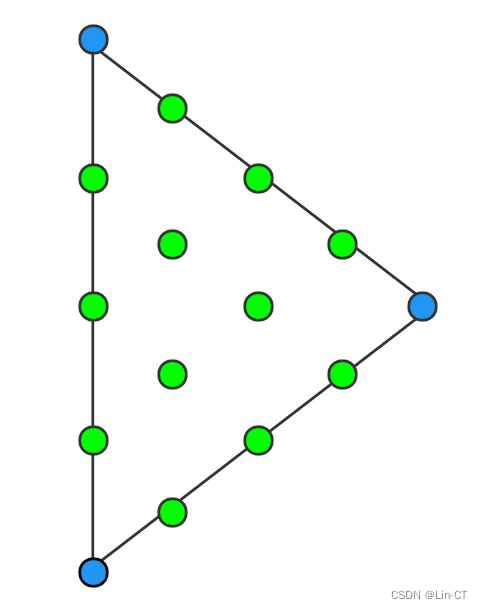
接着切换为中间三个无人机发射信号，以同样方式继续调整各无人机位置。多次交替这两种信号发射方案，使得在切换方案时飞机的位置偏差越来越小，完成定位。

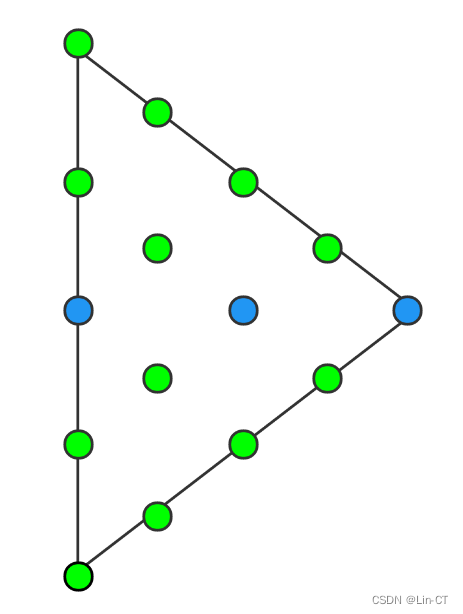
其中在接收信号飞机的定位可以参考上一大题的方案构建模型函数，无人机向α角标准化的方向移动，不断调整，得到整体的最优解。