现代密码学

【考后感悟】还是得注重简答题，需每个密码算法都要有所了解（有些难的可以不用了解完整算法过程，估计考不上？），并对几个重要密码算法（重点下面会讲）着重复习（会做大题计算）

✍Created by Sikevin in UESTC

【注】：复习本门课前需要有信息安全数学基础，可以查看博主主页的《信息安全数学复习》一文。

✍博客主页：电子科大不知名程序员

【核心重点算法】：DES算法、RSA、ElGamal、ECC算法、DH算法、Shamir门限方案。

1、引言

什么是密码？采用特定变换的方法对信息等进行加密保护、安全认证的技术、产品和服务

什么是密码学？密码学是研究编制密码和破译密码的技术科学

系统的保密性不依赖于对加密体制或算法的保密，而依赖于密钥。

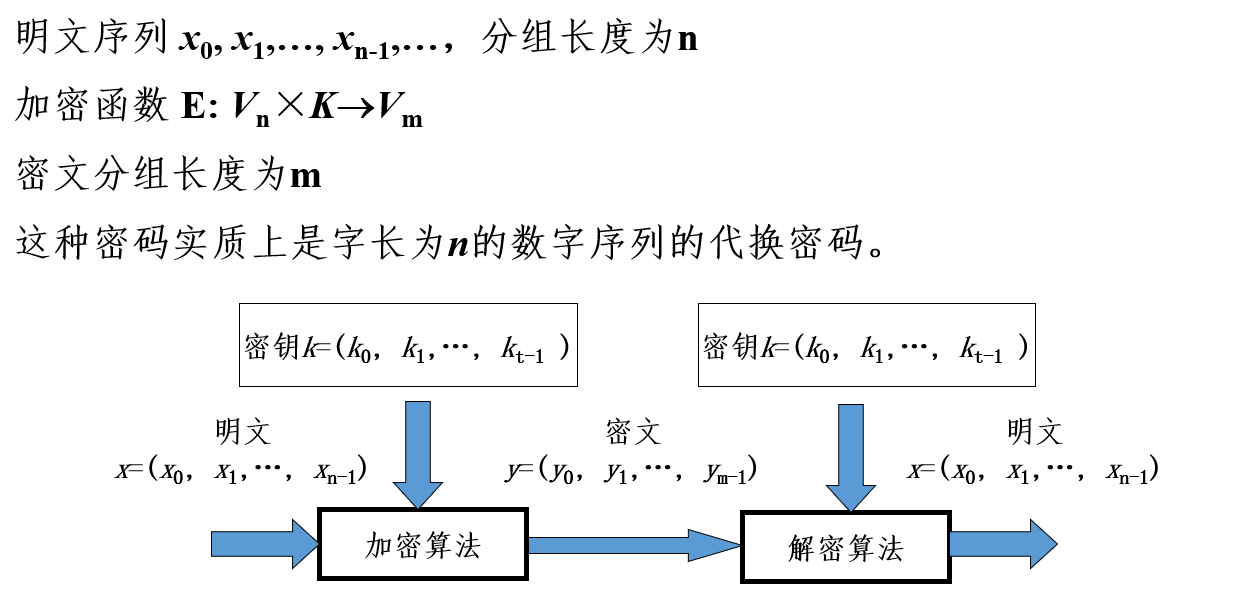
保密系统：

一个保密系统由：明文空间、密文空间、密钥空间、加密算法、解密算法构成。

①系统不可破

②保密性依赖于密钥**（Kerckhoffs假设）**

③加密解密算法适用密钥空间中的所有元素

④方便实现、使用

Kerckhoffs假设：假定密码分析者和敌手知道所使用的密码系统。即密码体制的安全性仅依赖于对密钥的保密，不应依赖于算法的保密

无条件安全与计算上安全：

计算上安全：

破译密文的代价超过被加密信息的价值。

破译密文所花的时间超过信息的有用期。

2、分组密码

分组密码应该满足的需求：

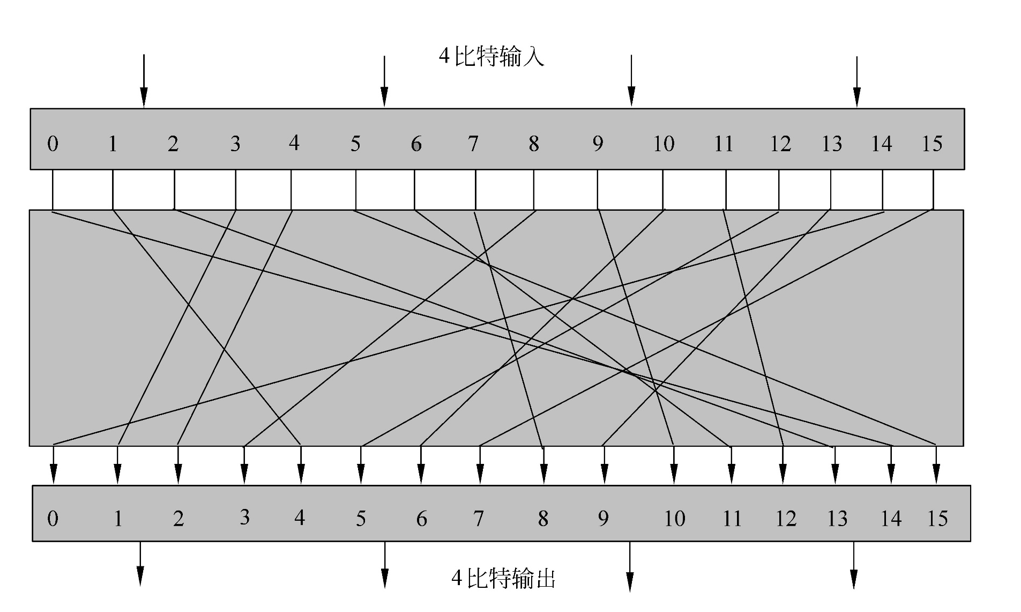
分组N要足够大，否则就等价于古典的代换密码

对n比特的代换结构，密钥的大小是n×2^n比特（n比特的分组长度，有2^n种情况）

代换网络：理解成是一种代换关系

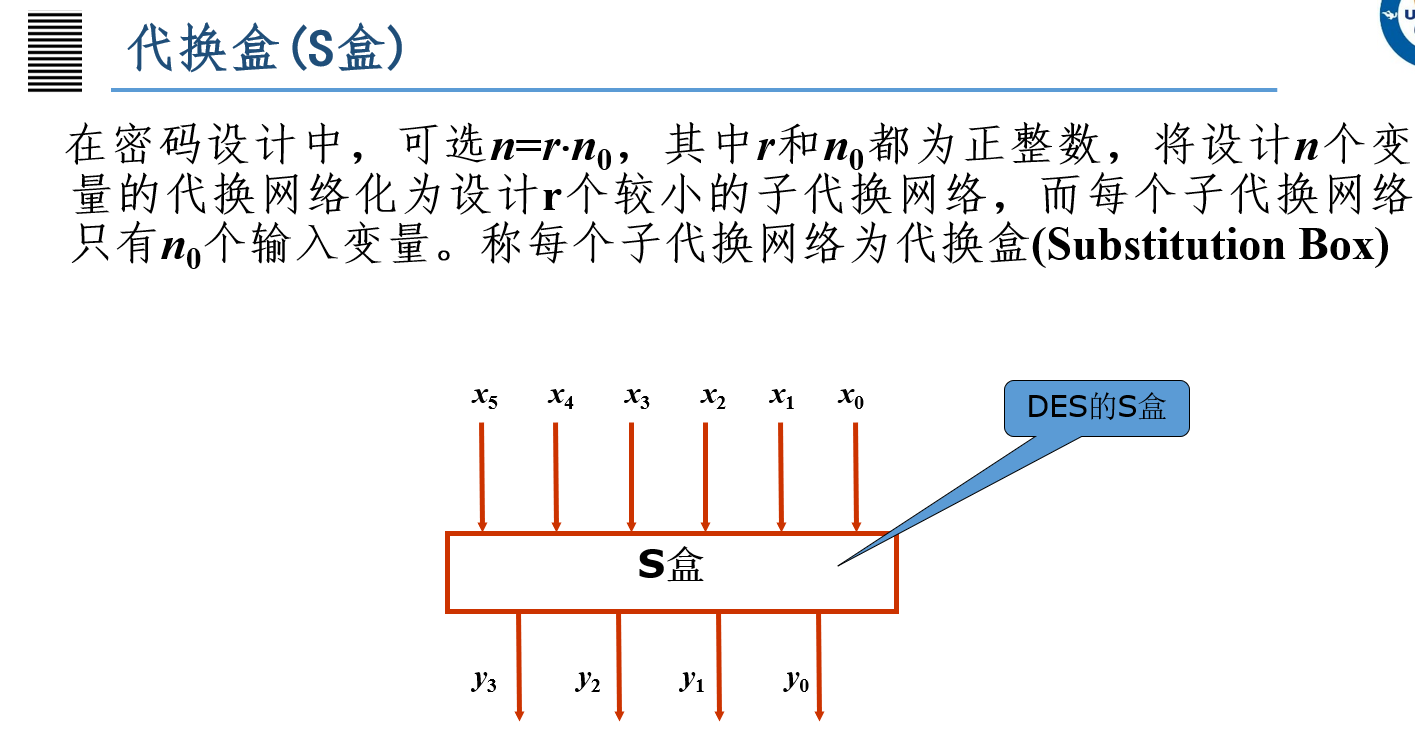
乘积密码指顺序地执行两个或多个基本密码系统，使得最后结果的密码强度高于每个基本密码系统产生的结果

Feistel算法

算法要易分析，软件要易实现

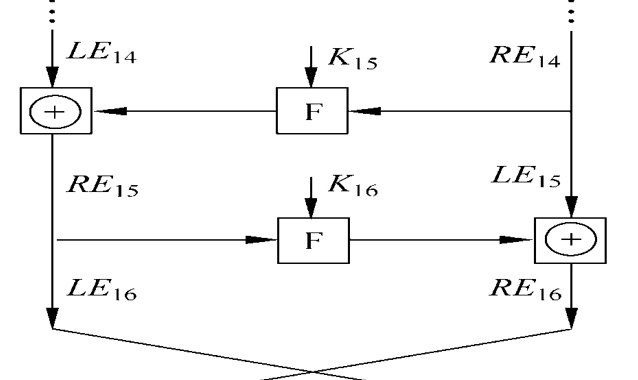
Feistel解密过程本质上和加密过程是一样的，算法使用密文作为输入

但使用子密钥Ki的次序与加密过程相反，即第1轮使用Kn，第2轮使用Kn-1，……，最后一轮使用K1。这一特性保证了解密和加密可采用同一算法。

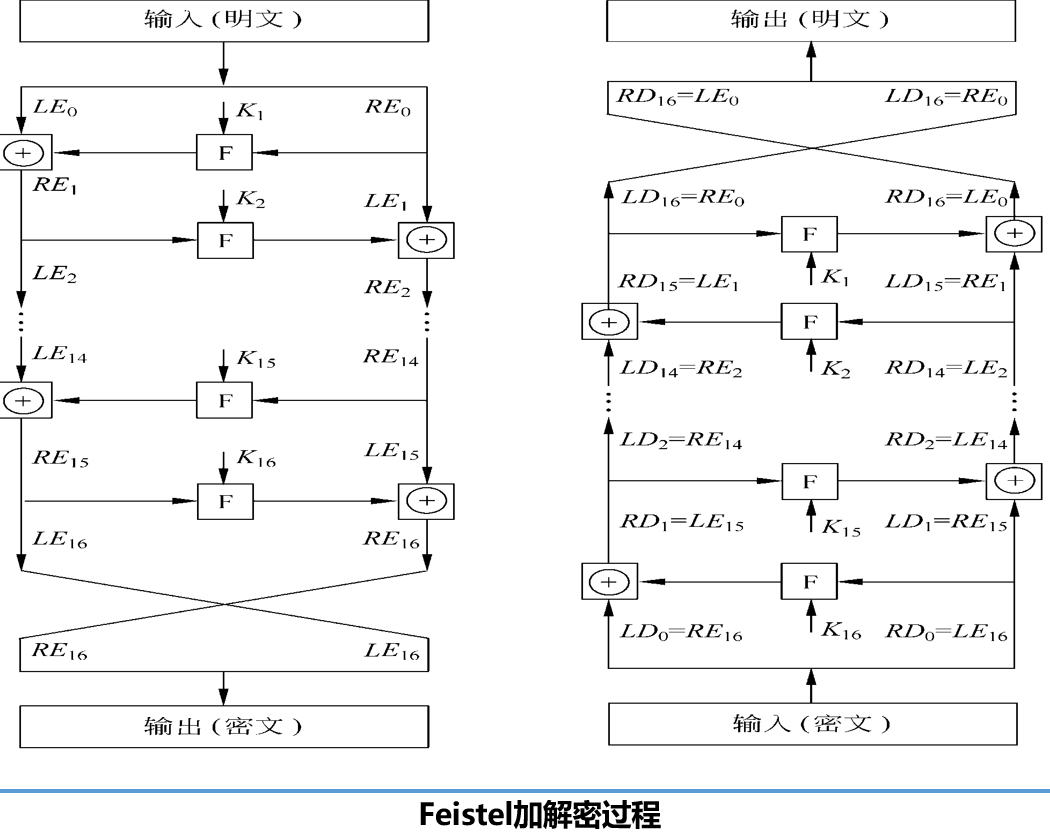
加密时：

美国制定数据加密标准简况

①高安全性

②易理解

③安全性取决于密钥

④适用于所有用户、多场景

⑤高效、经济、有效、可出口

DES算法

流密码加密是逐字节加密，而DES采用的是块加密，对每个分组进行加密后在合并到一起形成密文

分组长度：64比特

密文长度也为64比特

密钥长度为64比特，其中有8位奇偶校验位，因此有效的密钥长度为56比特

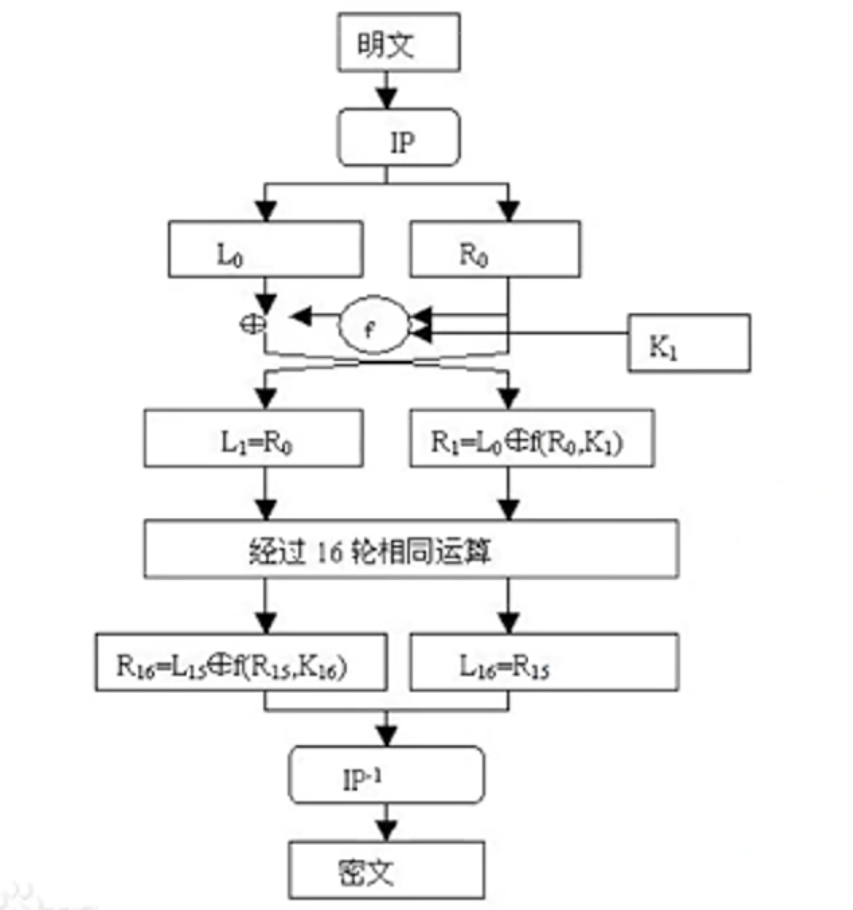
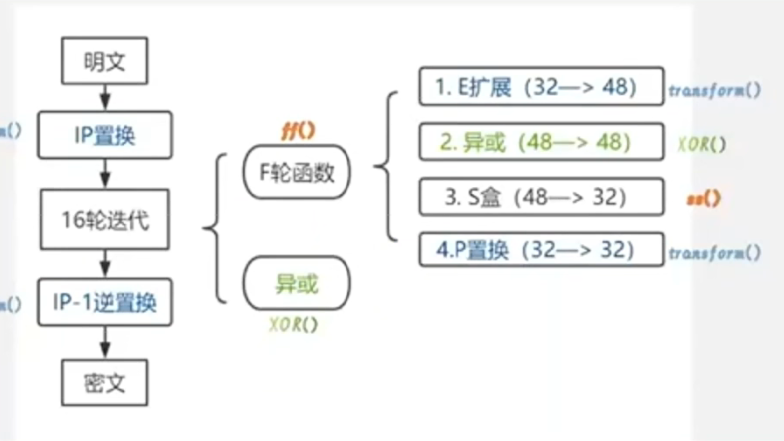
过程：

1、初始ip置换

将64比特明文的位置进行置换，得到一个乱序的64比特明文组

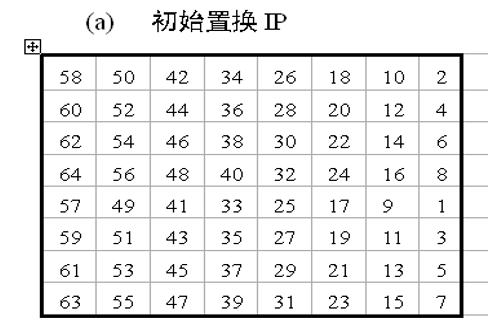
其中的数字代表原来的明文序列对应位置的放在当前位置；例如58表示原序列的第58个比特位放在放到第一位去

2、16轮迭代

①首先对于分组的64比特明文，分成左右两组（32比特）

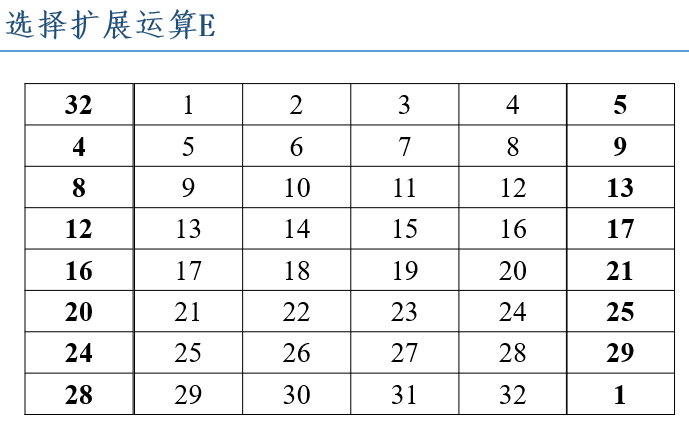
②密钥有效位为56比特，而密钥经过处理后，使用的是48比特的密钥，左右两组32比特，因此需要E扩展成48比特长度

首先将1到32比特用4行8列的矩阵按顺序写出，然后在左右两边进行扩展，左边扩展就是原矩阵最左边的一列的位置数减一，1没有办法减，就将第32位的值放在1的左边。而右边扩展就是原始矩阵最右边一列的位置加一，32右边放位置1的值。这样32比特就扩展成了

③将扩展好的明文（48比特）与48比特的密文进行异或操作（加密）

④由于明文32位被扩展成48位，因此需要使用S盒还原成32比特位

这里是6进4出的S盒

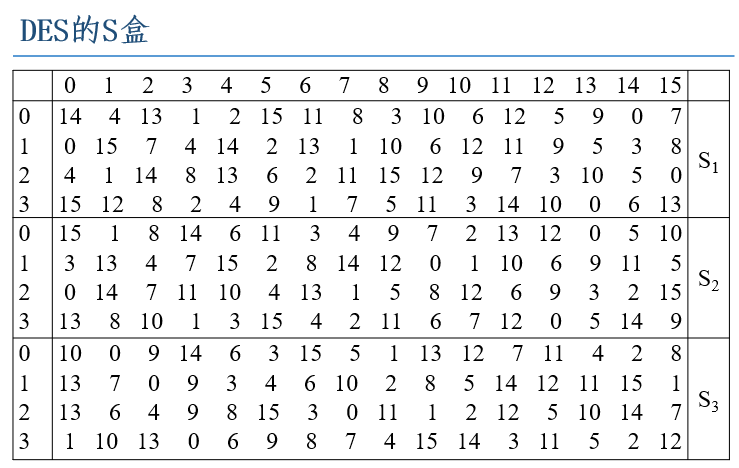
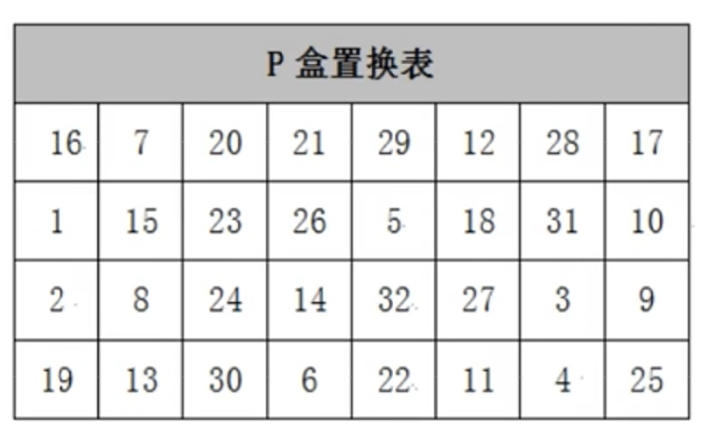
⑤S盒所得结果再进行P盒置换

3、密钥生成

密钥有64位，除去8比特奇偶校验位还有56位

①种子密钥，红色代表校验位：

②除去校验位后，进行置换选择1（PC1）：

③形成了56比特：

④分成C0和D0两部分，分别为28比特位

⑤C0和D0根据密钥计算逻辑进行循环左移得到C1和D1

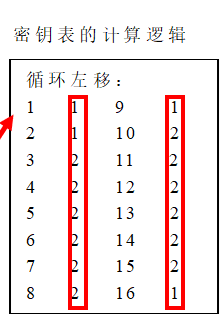
⑥C1和D1拼接—>置换表—>左移—>C2、D2—>再重复以上过程

DES是一种确定性算法。

4、DES的安全性

DES是不安全的！

密钥：

DES存在弱密钥和半弱密钥。所谓弱密钥指的是在同一密钥下加密两次为恒等变换，DES存在4个弱密钥

1. 0101010101010101（十六进制表示：0x0101010101010101）
2. FEFEFEFEFEFEFEFE（十六进制表示：0xFEFEFEFEFEFEFEFE）
3. E0E0E0E0F1F1F1F1（十六进制表示：0xE0E0E0E0F1F1F1F1）
4. 1F1F1F1F0E0E0E0E（十六进制表示：0x1F1F1F1F0E0E0E0E）

轮密钥的产生是原始密钥在置换选择1后，分成左右两半，然后进行循环移位，最后通过置换选择2输出轮密钥，因此只要左右两边循环移位后仍相同即可

只要28比特全零或全1就可满足要求。因此有四个：

1是全零

2是左边28比特为0，右边28比特为1

3是左边28比特为1，右边28比特为0

4是全1.通过逆置换选择1

再添加上奇偶校验位就可得到左边这四个弱密钥。弱密钥下同样使DES在选择明文攻击下的搜索量减半。不过，如果随机地选择密钥，弱密钥所占比例极小，而且稍加注意就不难避开。因此，弱密钥的存在不会危及DES的安全性。

所谓半弱密钥指的是一些密钥对，k1和k2互不相同，但是其加密出来的明文是一样的，或者换句话说用k1加密的密文可以用k2来解密。

3DES

DES由于其密钥较短，安全性不高，因此人们希望采用多重加密的方式来增大其密钥空间，从而提高其安全性。

多重DES就是使用多个密钥利用DES对明文进行多次加密。使用多重DES可以增加密钥量，从而大大提高抵抗穷举密钥搜索攻击的能力

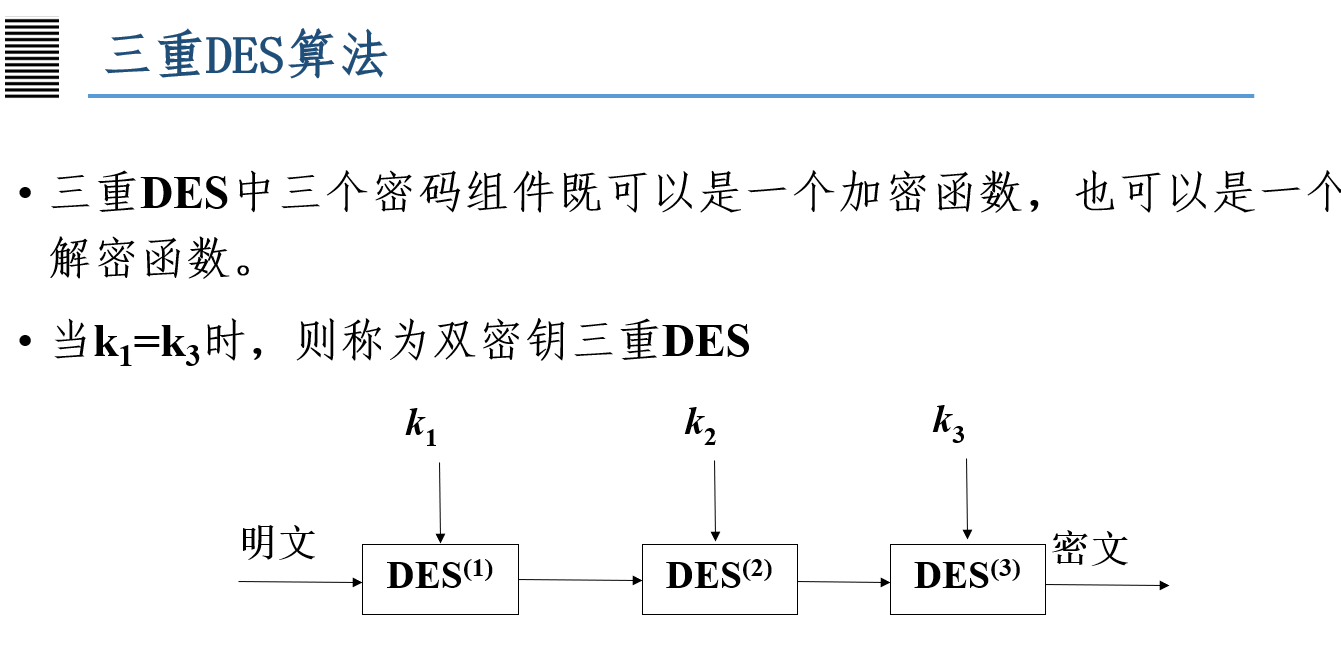
此方案仍有足够的安全性

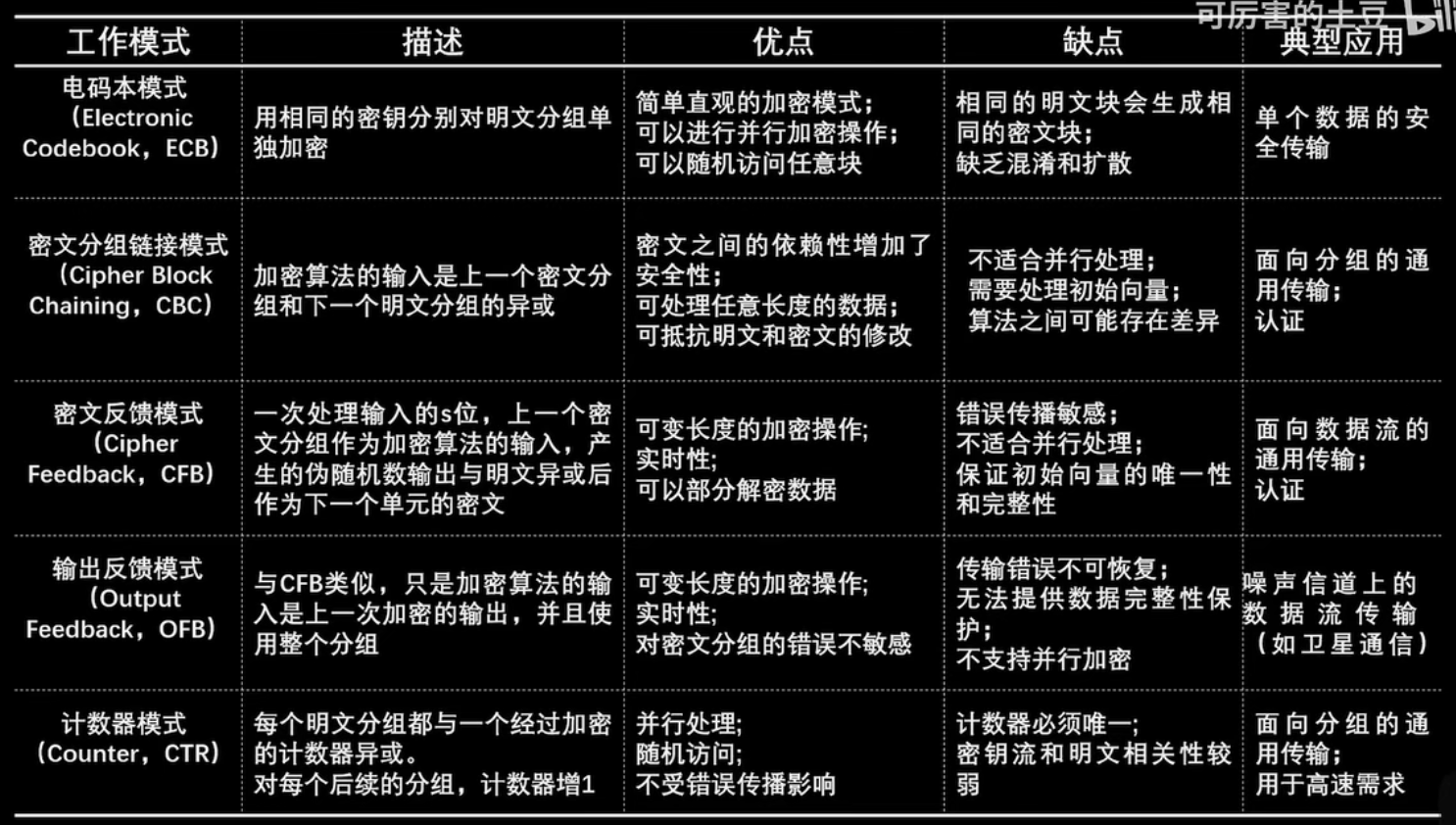
分组密码的工作模式

①电码本(ECB)模式

用相同的密钥分别对明文分组加密

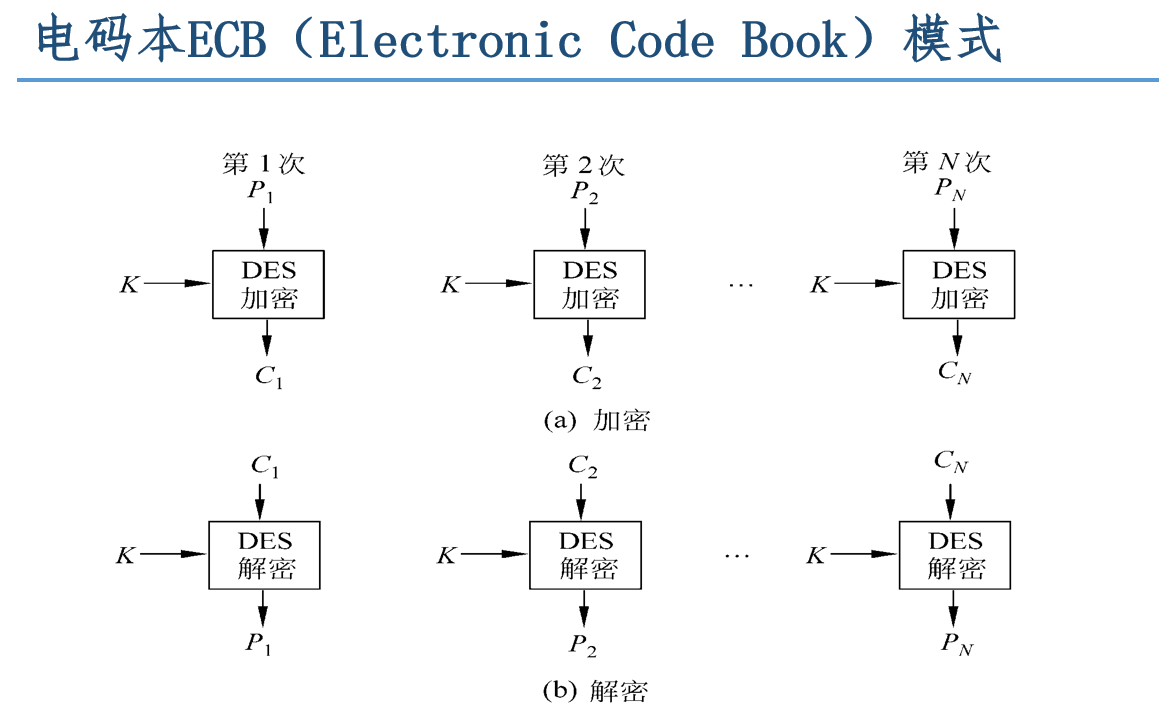
优点：对每个数据块独立加密，可并行加密

缺点：相同明文会产生相同密文，不具备数据完整保护性

同一明文组总产生同样的密文组。这会暴露明文数据的格式和统计特征。明文数据都有固定的格式，需要以协议的形式定义，重要的数据常常在同一位置上出现，使密码分析者可以对其进行统计分析、重传和代换攻击

即用来加密短的消息

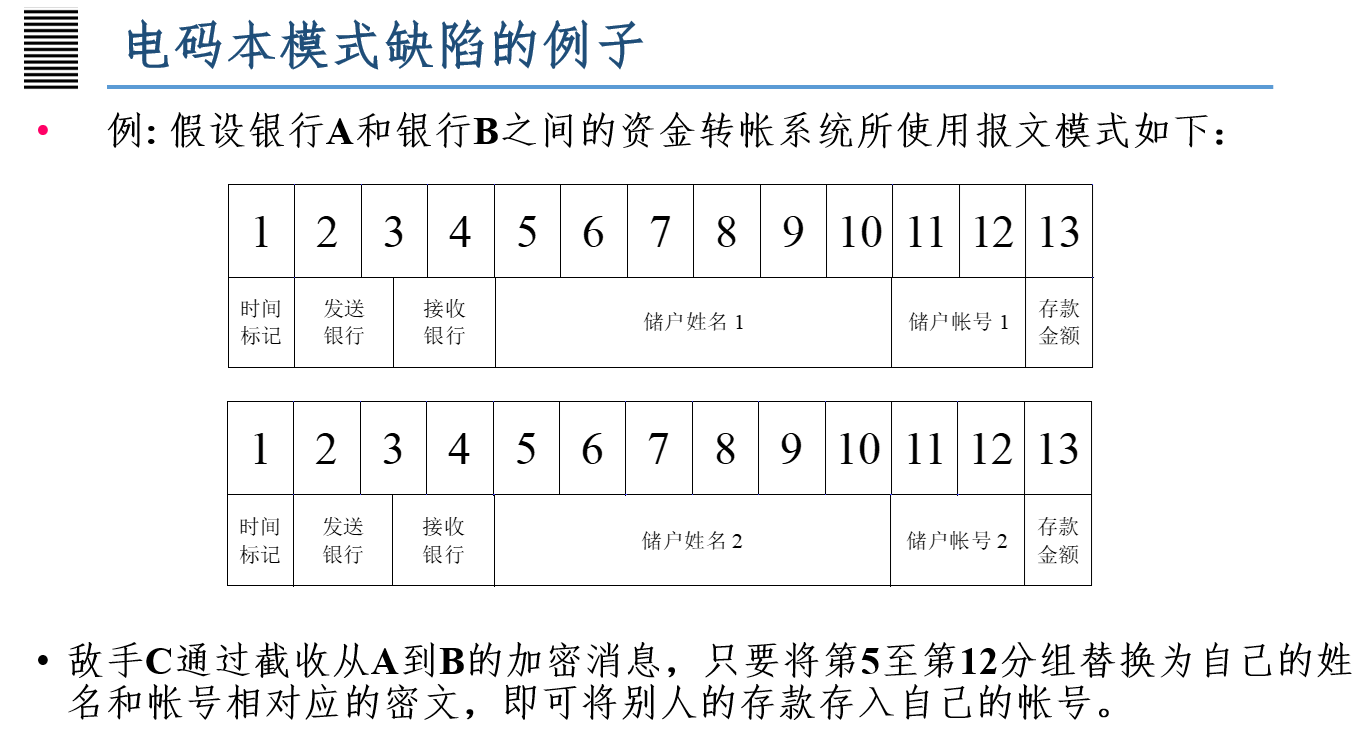
②密码分组链接CBC（Cipher Block Chaining）模式

加密算法的输入是上一个密文分组和下一个明文分组的异或

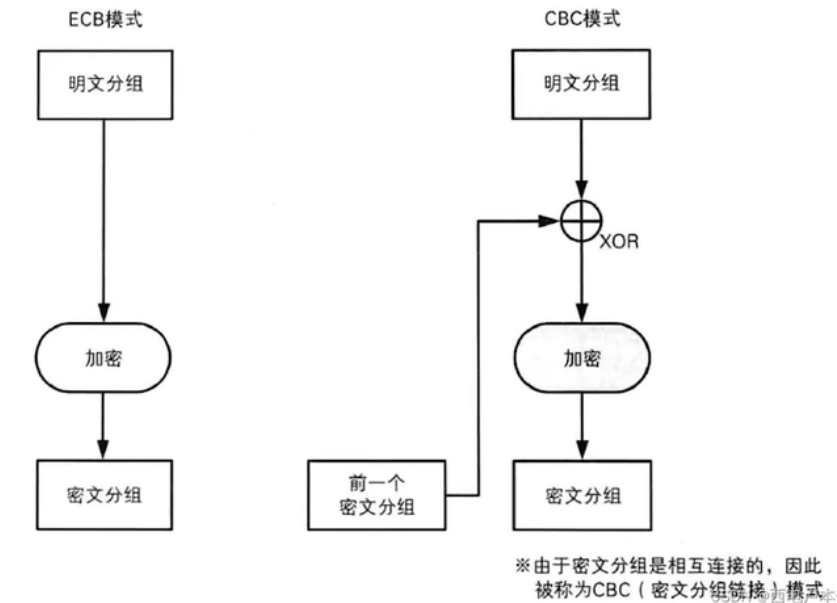
如果有一块密文分组在传输中发生了错误，会不会影响其他的分组解密？会影响多少个分组？这就是分组密码中所谓的错误传播。很显然，比如C1错了，P1自然是错的，而且P2也是错的，而由于C2没有出错，所以P3不会出错，也就是CBC模式的错误传播长度为1，也就是除了自身受影响外，最多只有一个分组受其影响。

③密码反馈CFB（Cipher Feedback）模式

将前一个密文块作为输入进行加密，生成一个密钥流，再与当前明文块进行异或运算得到密文块

流密码的工作模式

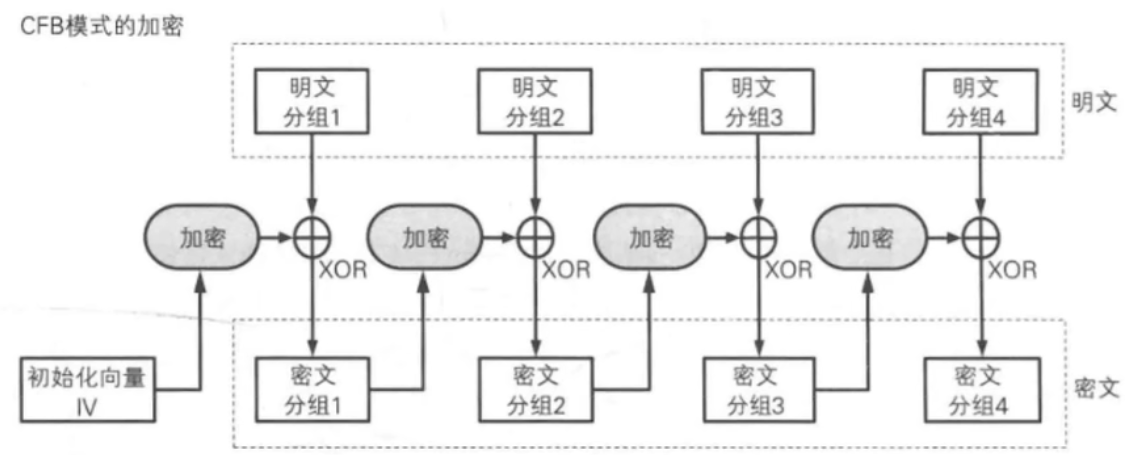
若待加密消息需按字符、字节或比特处理时，可采用CFB模式。并称待加密消息按 r 比特处理的CFB模式为 r 比特CFB模式。

④输出反馈OFB(Output Feedback)模式

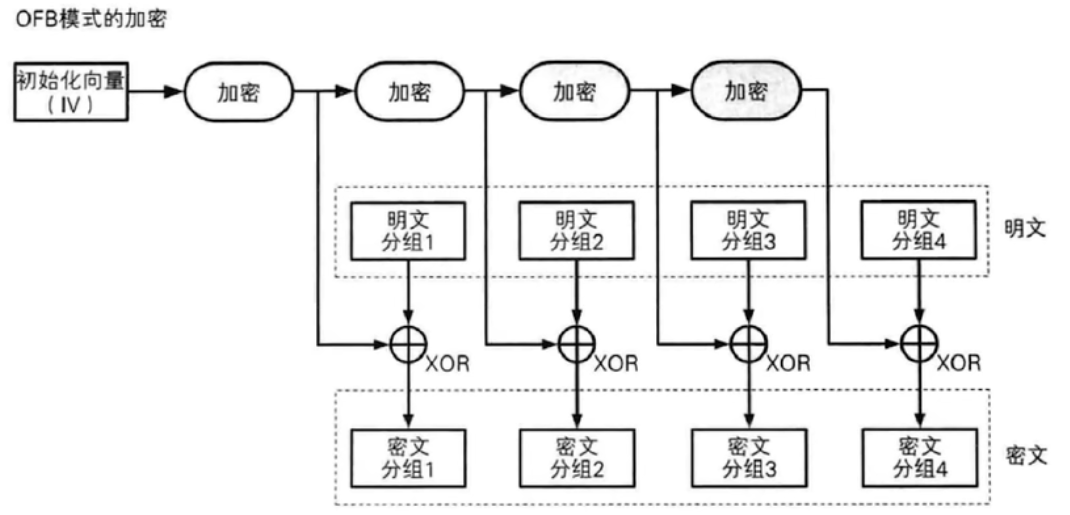
OFB模式在结构上类似于CFB模式，但反馈的内容是DES的输出而不是密文！

⑤计数器模式

每一个明文分组都与一个经过加密的计数器异或。对后续的分组，计数器增1

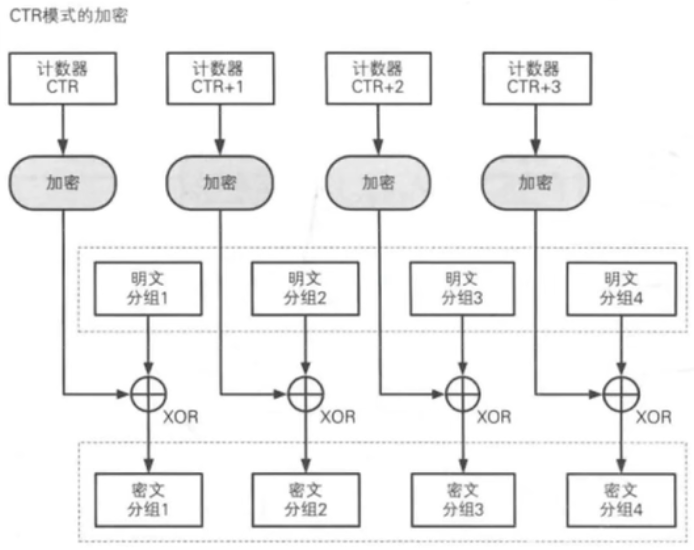
利用固定密钥k对自然数序列1,2,3,…,n, …加密，将得到的密文分组序列看作密钥流序列，按加法密码的方式与明文分组逐位异或的一种方式

利用这种方式可以产生伪随机数序列,其伪随机特性远比计算机产生的随机数的性质好

域

F是一个非空集合，定义了加法、乘法两个二元运算，对这两个运算封闭

GF(2^{8)中的元素可以表示为8位二进制数，即一个字节（byte）。加法和乘法是在GF(2}8)中定义的两个基本运算。

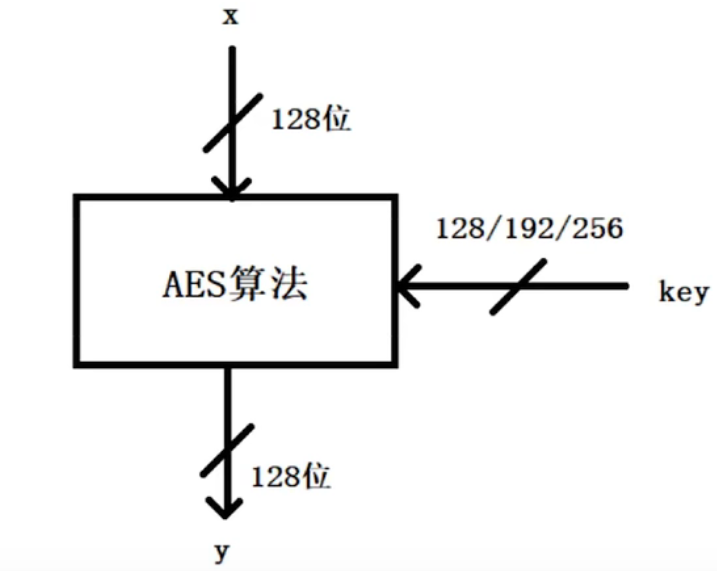
AES

AES属于分组加密算法

明文长度为固定的128位，密钥长度可以是128位、192位、256位

输入128位明文，为16字节的数据，16字节的数据组成一个4*4的矩阵，排列方式如下：

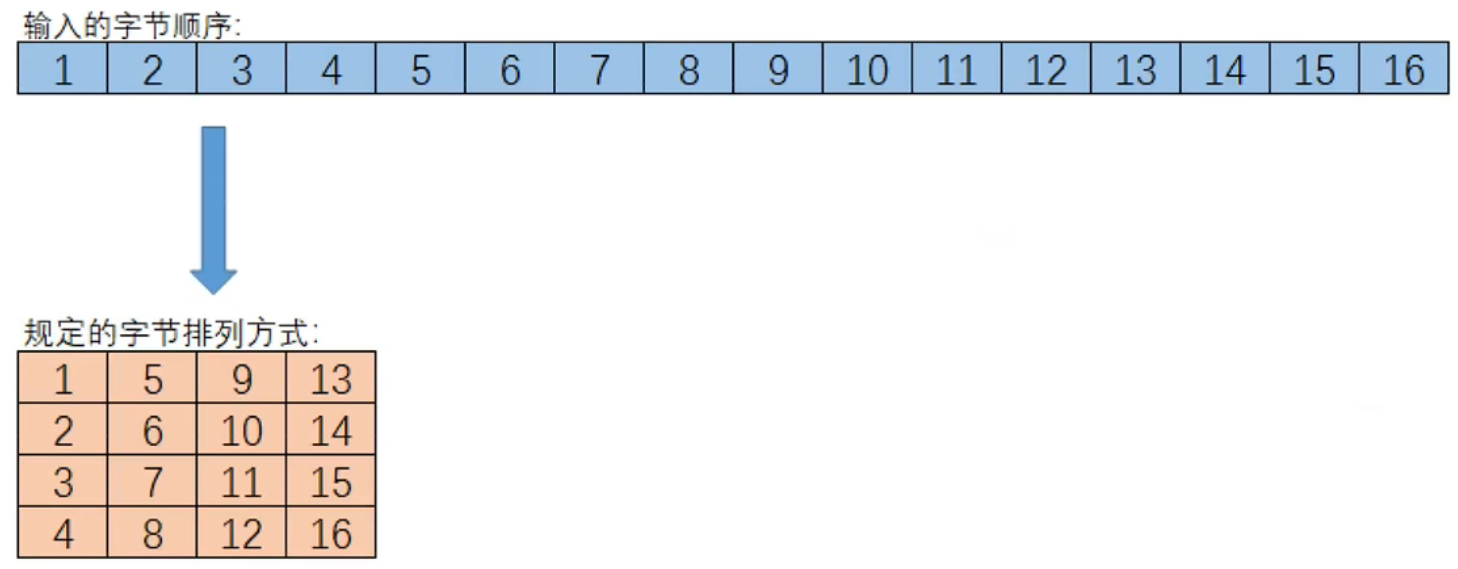
AES加密过程

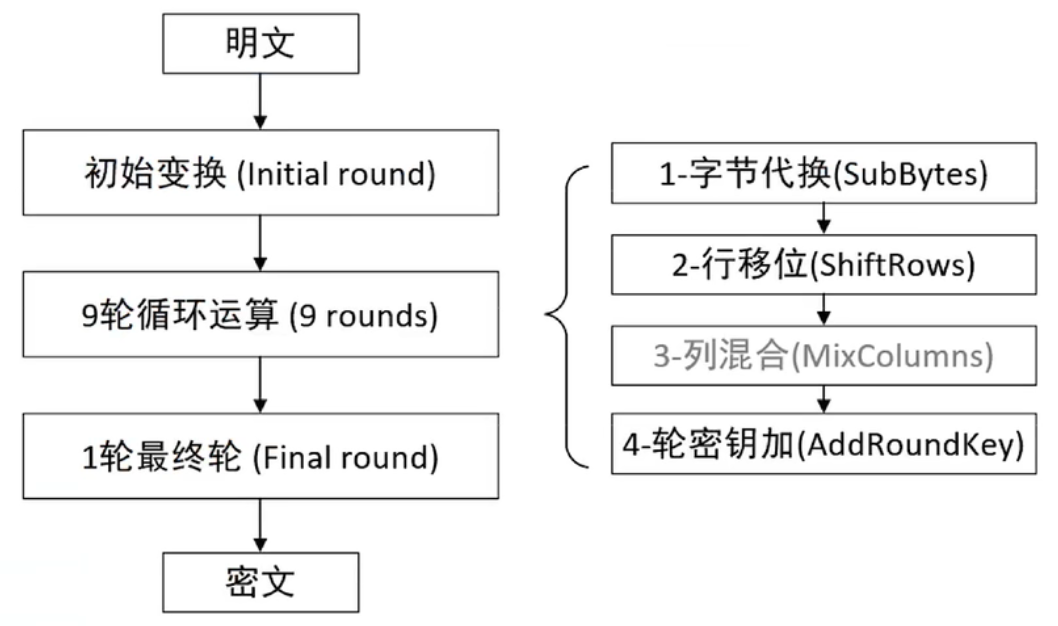
其中9轮循环运算时，执行1-4步骤，最后一轮（第十轮）只执行124步

1、初始变换

16字节固定长度的明文和M字节的密钥分别形成4*4的矩阵，执行异或操作：

具体如下：

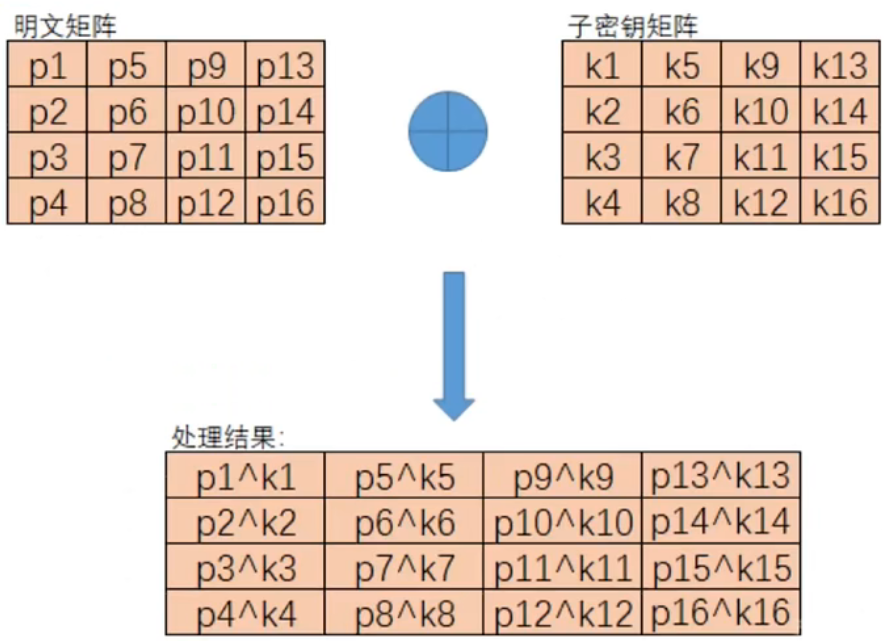
2、循环运算

①字节代换：处理初始变换后的4*4矩阵

对于矩阵中第一行第一列的数字19代表S盒第1行第9列的数字，将它与表中对应的数字替换（AES的S盒的使用）

②行移位

第一行不变，第二、三、四行分别向左移动1、2、3个字节

③列混合

将输入的4*4的矩阵左乘一个给定的4*4矩阵

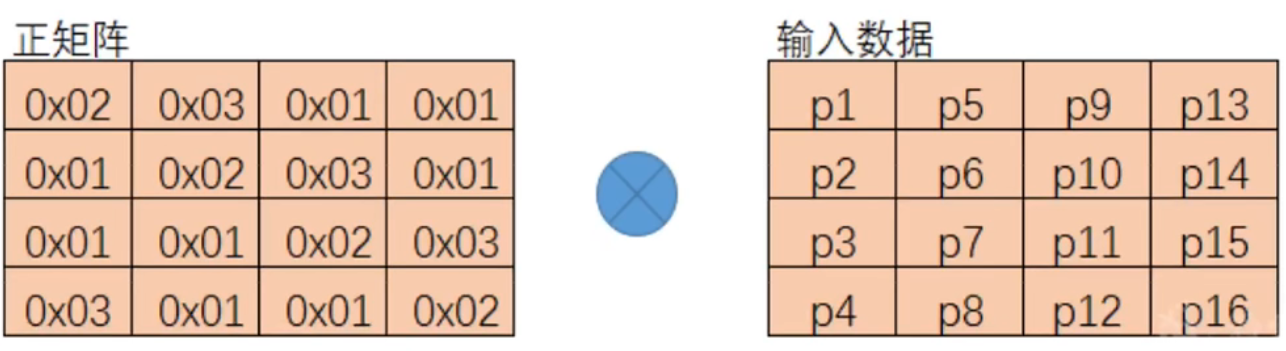
这里定义的乘法运算不是代数乘法运算！

④轮密钥加

这里有个概念：轮密钥；轮密钥是通过初始密钥通过某种方式生成的；下图展示了由初始密钥生成的轮密钥，具体生成方式不作阐述

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bNmy7aNf-1687273027747)(https://gitee.com/how-vague-and-fragile-love-is/images/raw/master/img2/image-20230605154352671.png)]

将前面所得的4*4矩阵与该轮对应的轮密钥进行异或操作

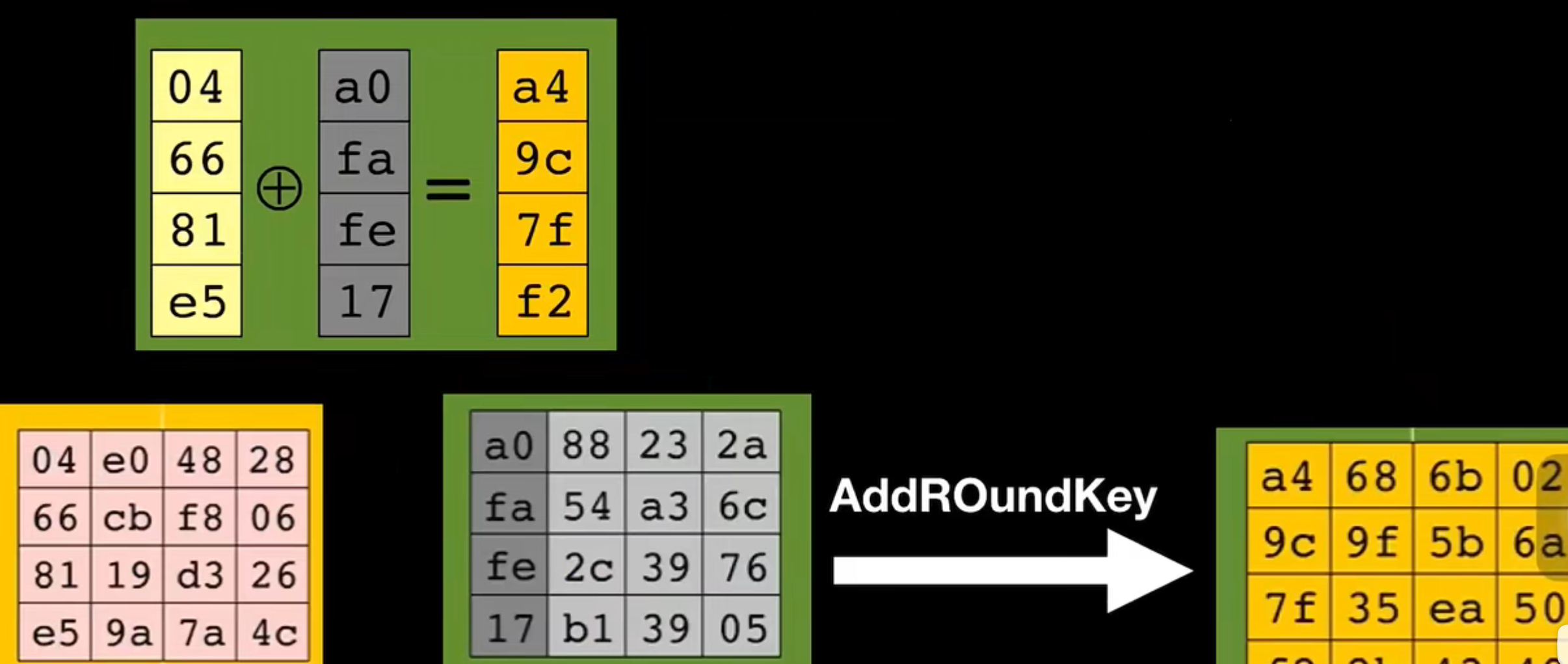
经过9轮循环和一个最终轮，得到了最终的密文

SM4

SM4密码算法是一个分组算法

分组长度为128比特，密钥长度为128比特；字代表长度为32比特的字符串，因此分组和密钥长度为4字

加密过程：

1、32轮迭代

已知明文输入X0、X1、X2、X3，依次计算出X4-X35的字（32轮运算）

生成方式如下：

计算时：由轮函数F来计算的；其中F运算中又包含一个T运算

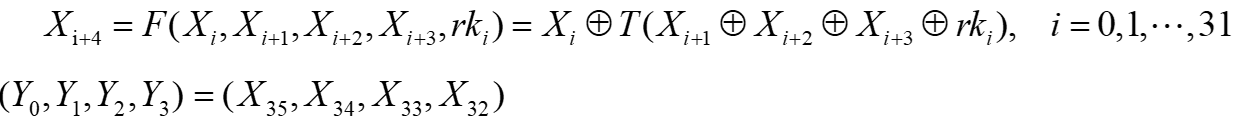
每轮都涉及到一个轮密钥，轮密钥由每个32比特的加密密钥生成。

2、反序变换

反序变化就是将计算出的结果X32-X35倒序

3、流密码

流密码基本思想

流密码(stream cipher)是一种重要的密码体制，明文消息按字符或比特逐位加密；流密码也称为序列密码(Sequence Cipher)

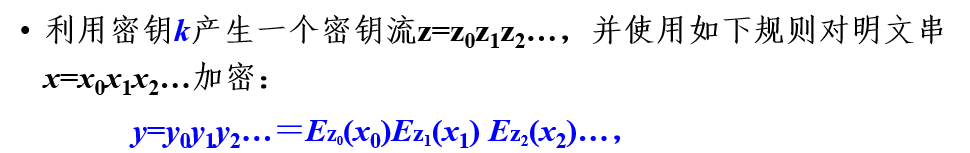
密钥流是由密钥流发生器产生的。

一种理想的加密方案，叫做一次一密密码（是加法流密码的原型）

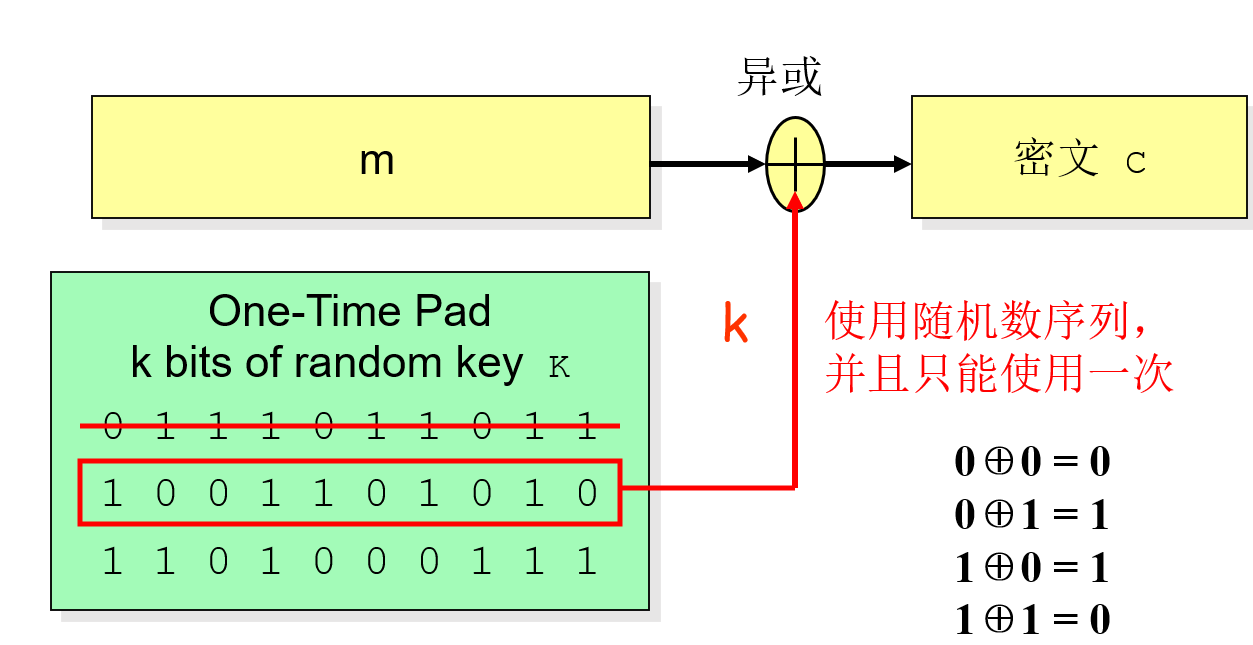
如果密钥用作滚动密钥流，则加法流密码就退化成一次一密密码。

密码设计者的最大愿望是设计出一个滚动密钥生成器，使得密钥经其扩展成的密钥流序列具有如下性质：

极大的周期

良好的统计特性

抗线性分析

二元序列的伪随机性

游程：

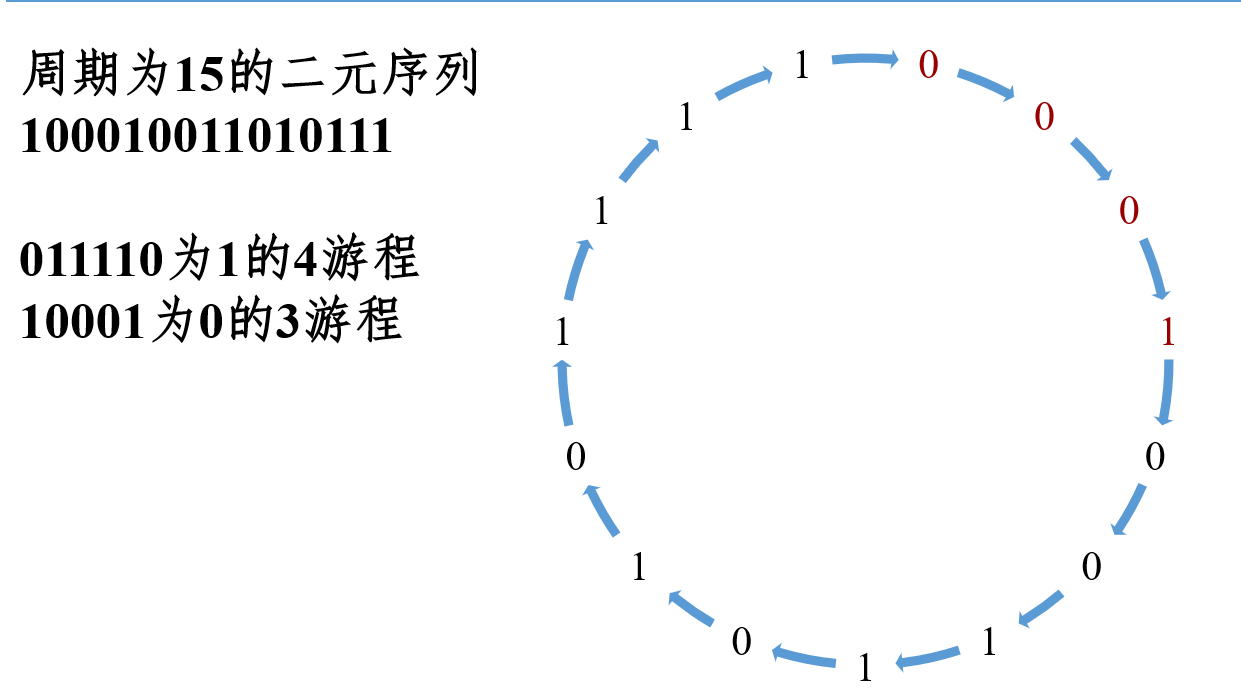
伪随机序列

伪随机序列还应满足的条件：

周期p要足够大，如大于10^50；

序列产生易于高速生成；

当序列的任何部分暴露时，要分析整个序列，提取产生它的电路结构信息， 在计算上是不可行的，称此为不可预测性。（决定了密码的强度，是流密码理论的核心。它包含了流密码要研究的许多主要问题，如线性复杂度、相关免疫性、不可预测性等等。）

线性反馈移位寄存器

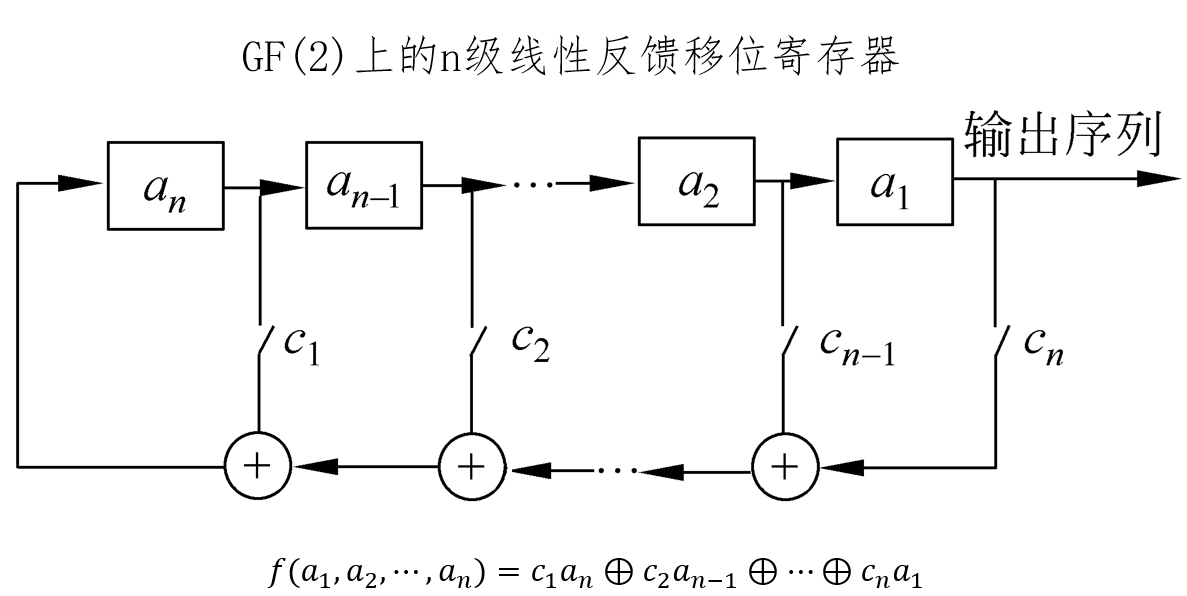
LFSR

n级LFSR的状态周期：<=2^n-1，周期达到最大值的序列称为m序列。

BM算法

求线性移位寄存器的线性综合解

作用：由寄存器的输出，反推寄存器的结构

3、公钥算法

公钥密码体制也被称为： 非对称密码体制

传统的对称密码算法有缺陷

①密钥分配问题：通信前需要通信信道协商加密密钥，这种通信信道很难实现

②任何两个用户都有共享的私密钥，密钥数目过于庞大，系统开销大

③没有签名功能（当主体A收到主体B的电子文挡时，无法向第三方证明此电子文档确实来源于B， 传统单钥加密算法无法实现抗抵赖的需求）

公钥密码的理论基础：

困难问题

RSA

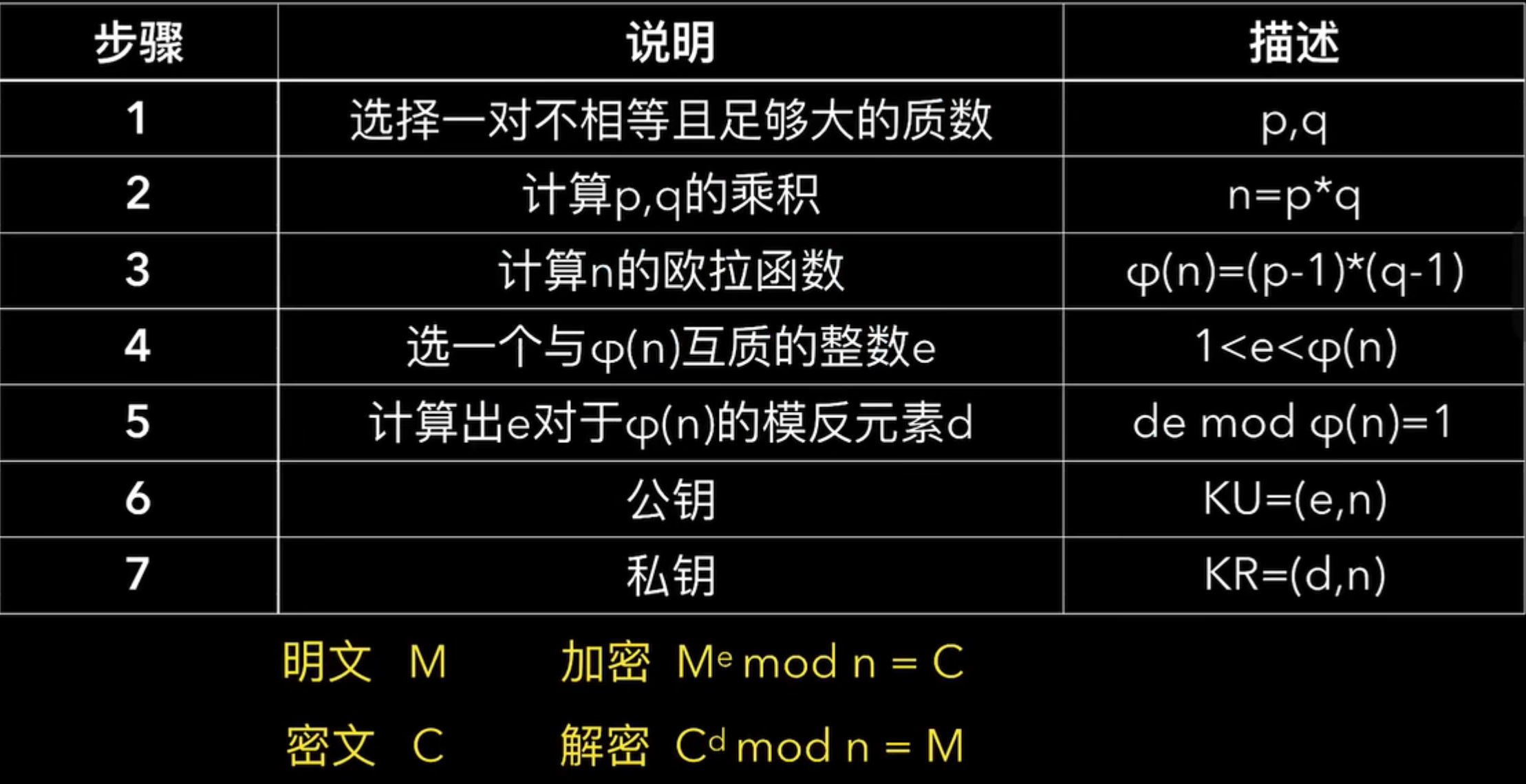
模反元素：逆元！

需要使用扩展欧几里得算法

RSA算法中的计算问题：

RSA的加密、解密过程都为求一个整数的整数次幂，再取模。如果按其含义直接计算，则中间结果非常大，有可能超出计算机所允许的整数取值范围。而用模运算的性质：

(a×b) mod n=[(a mod n)×(b mod n)] mod n

快速幂运算：

如何提高加、解密运算中指数运算的有效性。例如求x16，直接计算的话需做15次乘法。然而如果重复对每个部分结果做平方运算即求x，x2，x4，x8，x16则只需4次乘法

对于更一般的情况：

对于一串二进制数作为指数，在其**右边补0等于将这个数平方，在其右边补1等于将这个数平方后乘以底数 **

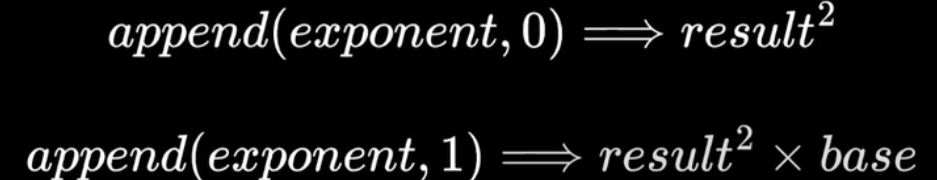
RSA的安全性是基于分解大整数的困难性假定，如果RSA的模数n被成功地分解为p×q，则立即获得φ(n)=(p-1)(q-1)，从而能够确定e模φ(n)的乘法逆元d，即d≡e-1 mod φ(n)，因此攻击成功。

ElGamal

①密钥产生过程： 选择一素数p以及小于p的随机数x， g是p的原根，计算y≡g^x mod p。

原根：

将求解出的原根带入，算出y

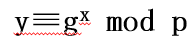
②加密过程

③解密过程

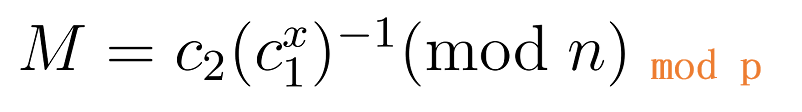
ECC算法

ECC算法基于椭圆曲线离散对数问题

椭圆曲线上两个点P和Q，k为整数，若给定k和P，计算Q很容易：

而给定P和Q，求k非常困难

①椭圆曲线的加法问题：

如上图，A+B代表经过A、B两点的直线与椭圆曲线的交点

椭圆曲线上定义的加法不是代数的加法！

②椭圆曲线的乘法问题：

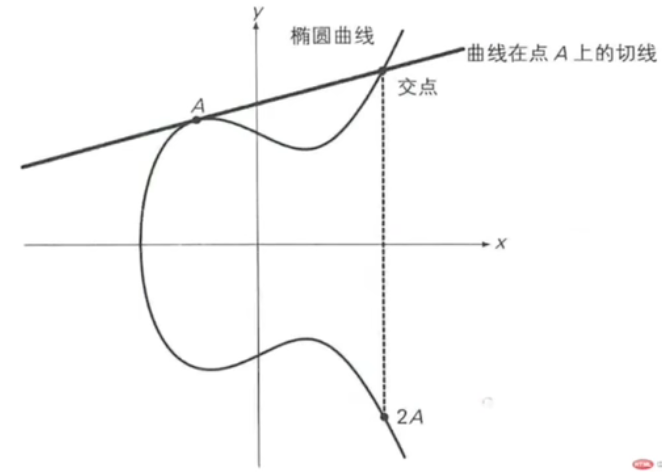
已知点A，要计算2A怎么算呢？2A=A+A，用加法的思路可以将A和A两点位置看成无线趋近，此时在A点处形成切线，切线与椭圆曲线相交的点即为2A点

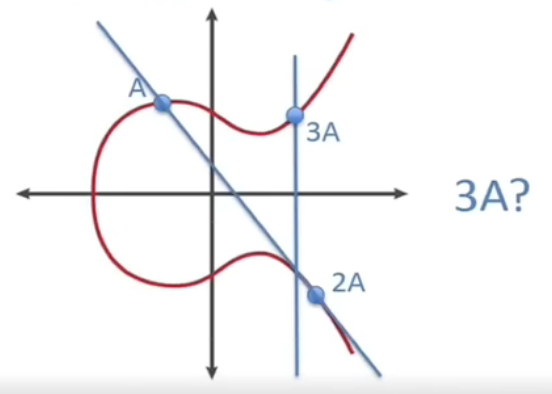
若要计算3A，可以看作3A=2A+A，即是2A点和A点所构成的连线与椭圆曲线的交点：

由此可见，对于椭圆曲线上的乘法问题：

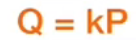
已知k点和P点计算Q点位置是容易的，而由于对于A、2A、3A他们的分布是无法预测的，因此想要通过已知的Q、P两点计算k是困难的！

③加密过程

④椭圆曲线是连续的，并不适合加密，将椭圆曲线定义在有限域上即可将椭圆曲线变成离散的点！

示例：

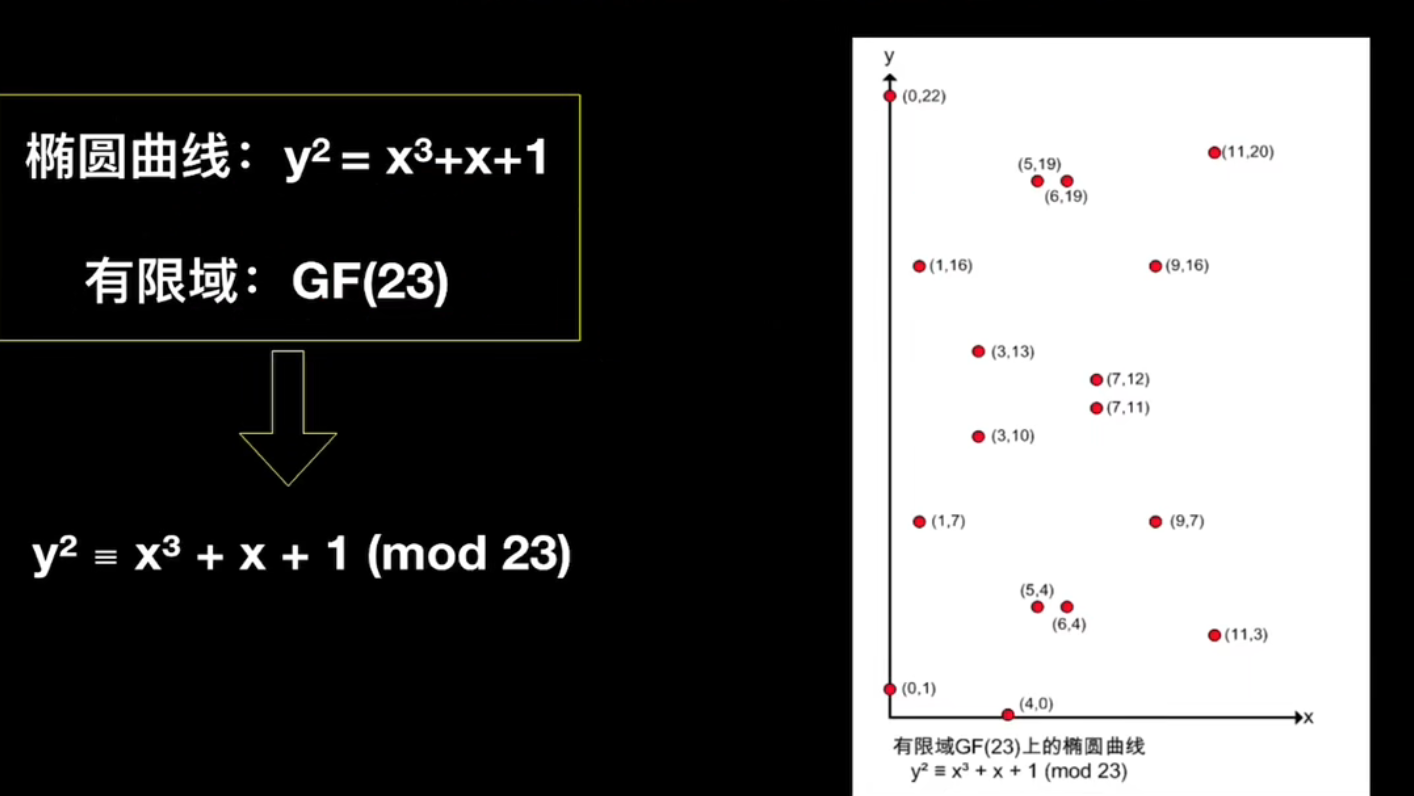
那么它的点是如何计算的呢？

计算示例如下：

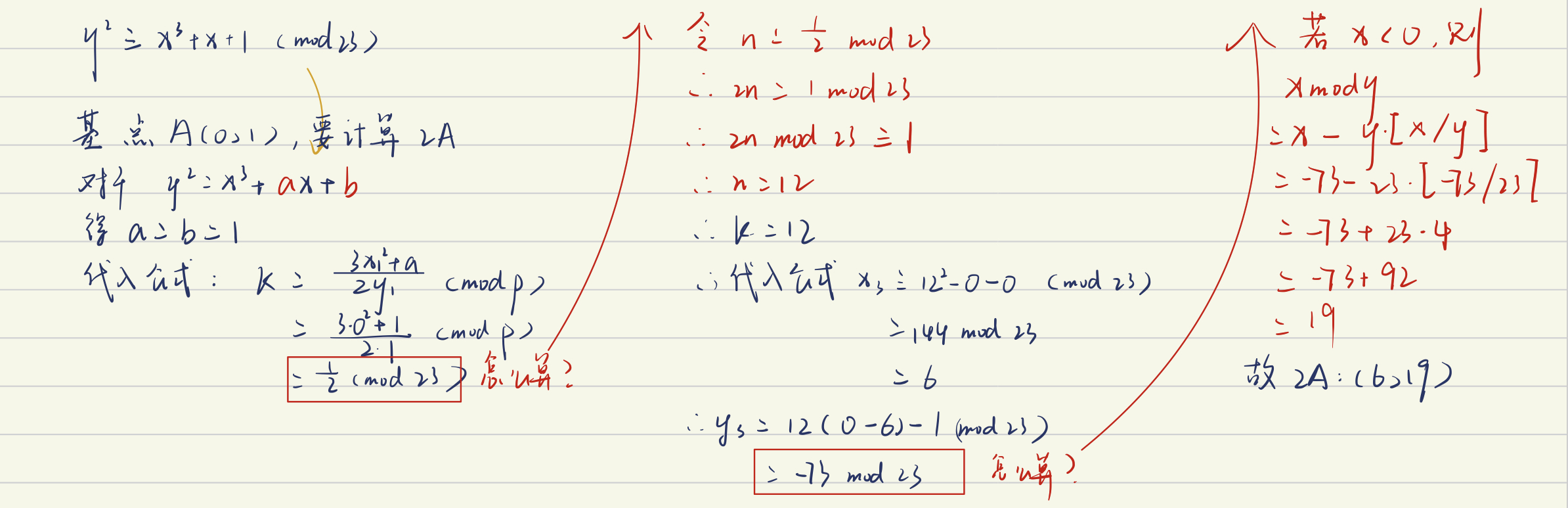
4、HASH函数

消息认证码

消息认证是一个过程，用以验证接收消息的真实性和完整性，同时还用于验证消息的顺序性和时间性。

消息认证机制需要产生认证符。

认证符：用于认证消息的数值。

认证符的产生方法：消息认证码MAC（message authentication code）和杂凑函数（hash function）两大类。

MAC函数与加密算法类似，不同之处为MAC函数不必是可逆的，因此与加密算法相比更不易被攻破

哈希函数

Hash函数的目的是为需认证的数据产生一个“指纹”

Hash函数的定义：将任意长的消息M映射为较短的、固定长度的一个值H(M)。

Hash函数H一般是公开的。

Hash函数的目的是为需认证的数据产生一个“指纹”，Hash函数应满足以下条件：

Hash函数函数的输入可以是任意长

Hash函数函数的输出是固定长

易于在软件和硬件实现

三个安全性的关系：

生日攻击

所谓哈希算法，即是试不同大小的输入imput得到固定长度的字符串舒服output

很显然，相同的输入，一定会得到相同的输出结果（雪崩效应）

然而，不同的输入，可能会得到相同的输出（哈希碰撞）

生日攻击：

当k=23时，P(365,23)=0.5073，即上述问题只需23人，人数如此之少。

若k=100，则P(365,100)=0.9999997，即获得如此大的概率。

之所以称这一问题是悖论是因为当人数k给定时，得到的至少有两个人的生日相同的概率比想象的要大得多。

SHA-1

算法的输入：小于2^64比特长的任意消息，分为512比特长的分组。

算法的输出：160比特长的消息摘要。

算法步骤：

①对消息的填充，让消息的长度L满足：

怎么补位呢？

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7zlUfBb9-1687273027756)(https://gitee.com/how-vague-and-fragile-love-is/images/raw/master/img2/image-20230604170001223.png)]

那么512-448=64，剩下的64位表示消息的长度

例如：

消息的长度为24位，64位留下作为表示消息的长度，那么512-64-24=424，因此424位就补位64位，表示消息长度，因此消息长度的最大值不能超过2^64

SM3

输入长度为l的消息m，其中输入数据长度小于2^64

输出长度为256bit的杂凑值

其中对消息m长度为l比特，也需要进行填充操作：（与SHA-1同样的填充方式）

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WAS0mSFt-1687273027757)(https://gitee.com/how-vague-and-fragile-love-is/images/raw/master/img2/image-20230604185047054.png)]

后续过程：（不管）

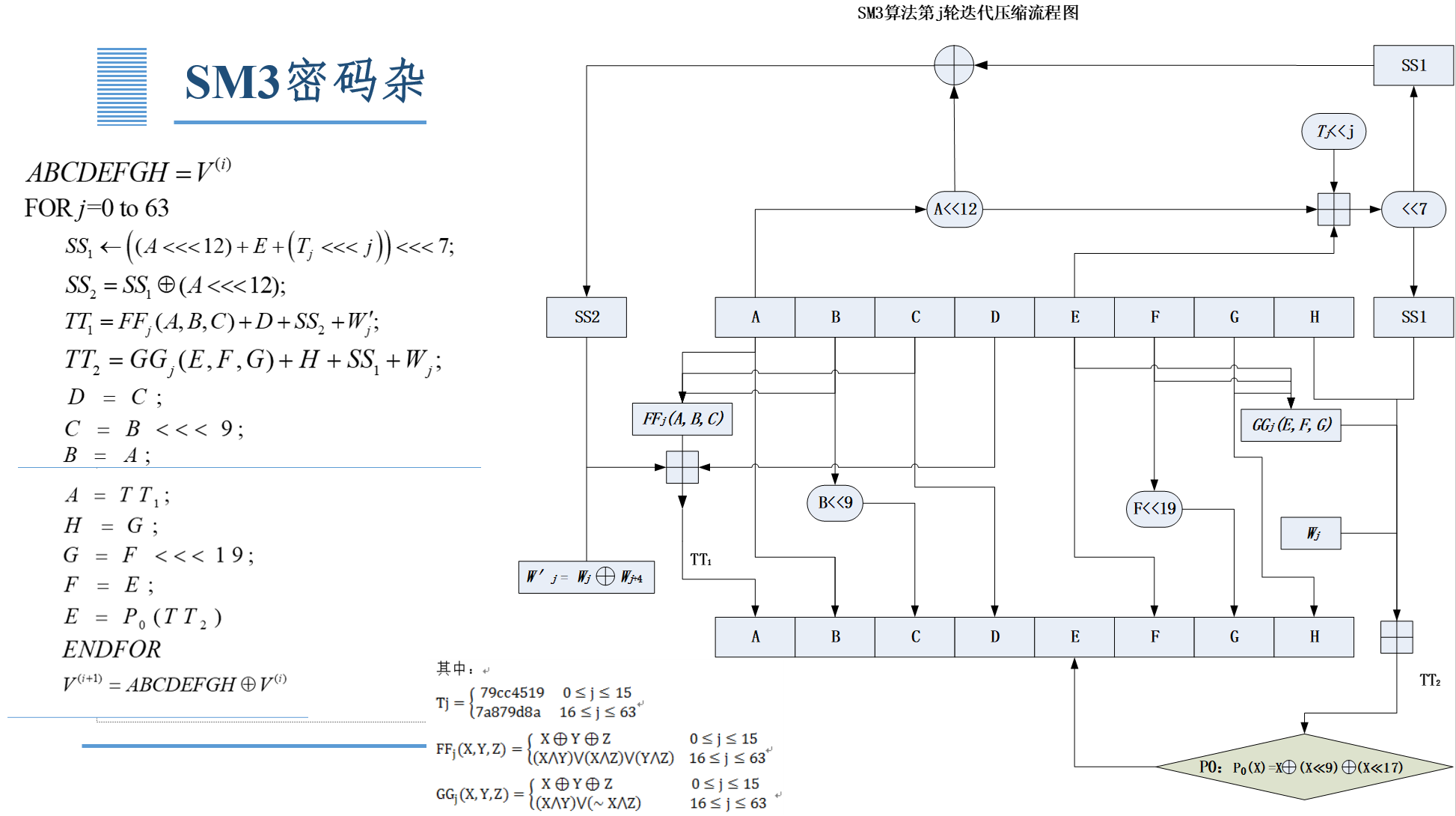
6、数字签名

数字签名(digital signature): 用于对数字消息签名，以防消息的伪造或篡改，也可用于通信双方的身份鉴别。

RSA数字签名

安全性：大数分解的困难性

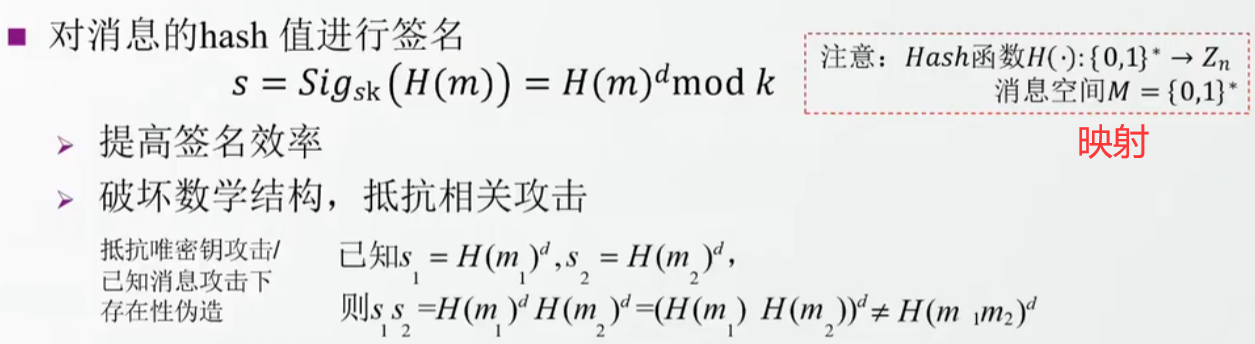
DSS数字签名标准

非确定性性算法：相同的密文在签名后得到的是不同的签名

基于求解离散对数的困难性

ElGamal签名

H（m）代表明文的哈希值

该签名算法基于的是离散对数问题是困难的

①如果 k 泄露，即使其他参数保持保密，攻击者可以使用相同的消息和已知的签名计算私钥 x。因此，为了确保签名的安全性，随机数 k 必须保持秘密并且每次签名都使用一个新的随机数。在实际使用中，可以通过伪随机数生成器来选择随机数 k，并确保生成的随机数是具有足够的随机性和安全性的。

②使用相同的 k 值签名不同的消息将使私钥泄露

交互证明系统

交互证明和数学证明的区别： 数学证明的证明者可自己独立地完成证明，而交互证明是由P产生证明、V验证证明的有效性来实现，因此双方之间通过某种信道的通信是必需的。

交互证明系统须满足以下要求：

① 完备性：若P知道某一秘密，V将接受P的证明。

② 可靠性：如果P能以一定的概率使V相信P的证明，则P知道相应的秘密。

7、密码协议

DH算法

DH算法属于公钥加密算法，公钥加密算法加密复杂，花费时间久。因此加解密数据时使用对称密码，然而对称密码需要一建立一个安全的通信，但没用哪个通信管道是完全安全的，因此密钥管理需要DH算法

用来使通信双方安全的交换密钥

核心公式：

基本原理：

Shamir门限方案

门限方案的一般概念：

秘密s被分为n个部分,每个部分称为shadow,由一个参与者持有，使得由k个或多于k个参与者所持有的部分信息可重构s；由少于k个参与者所持有的部分信息则无法重构s。

称为(k,n)秘密分割门限方案，k称为门限值、

Kerberos认证协议

会话过程：

一次性口令

在信息系统中常用用户名+口令（理解为密码）的方式证明身份，因此易猜的口令或缺省口令是一个验重的问题

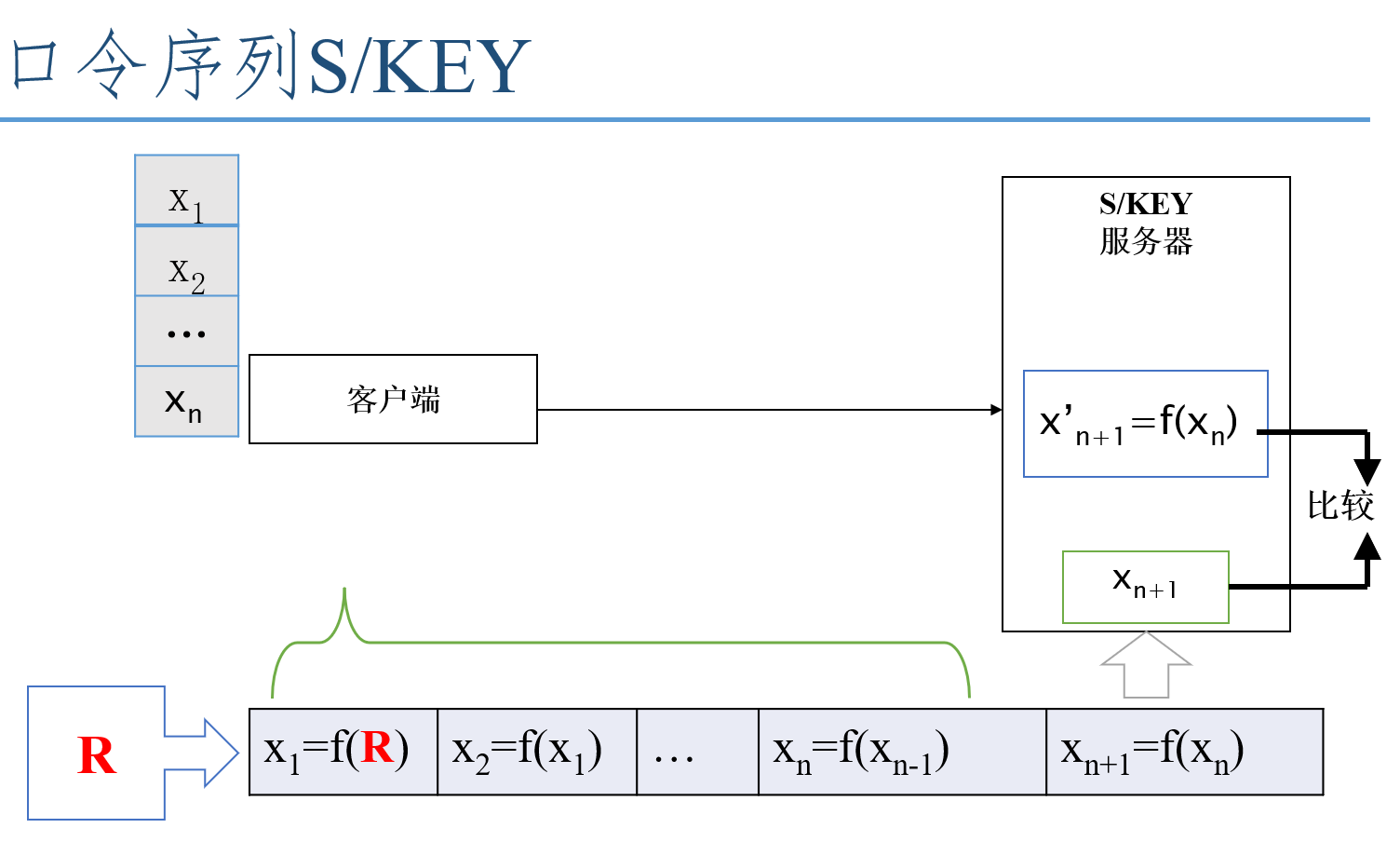
在登录过程中加入不确定因素，使每次登录过程中传送的信息都不相同

引入时间戳：