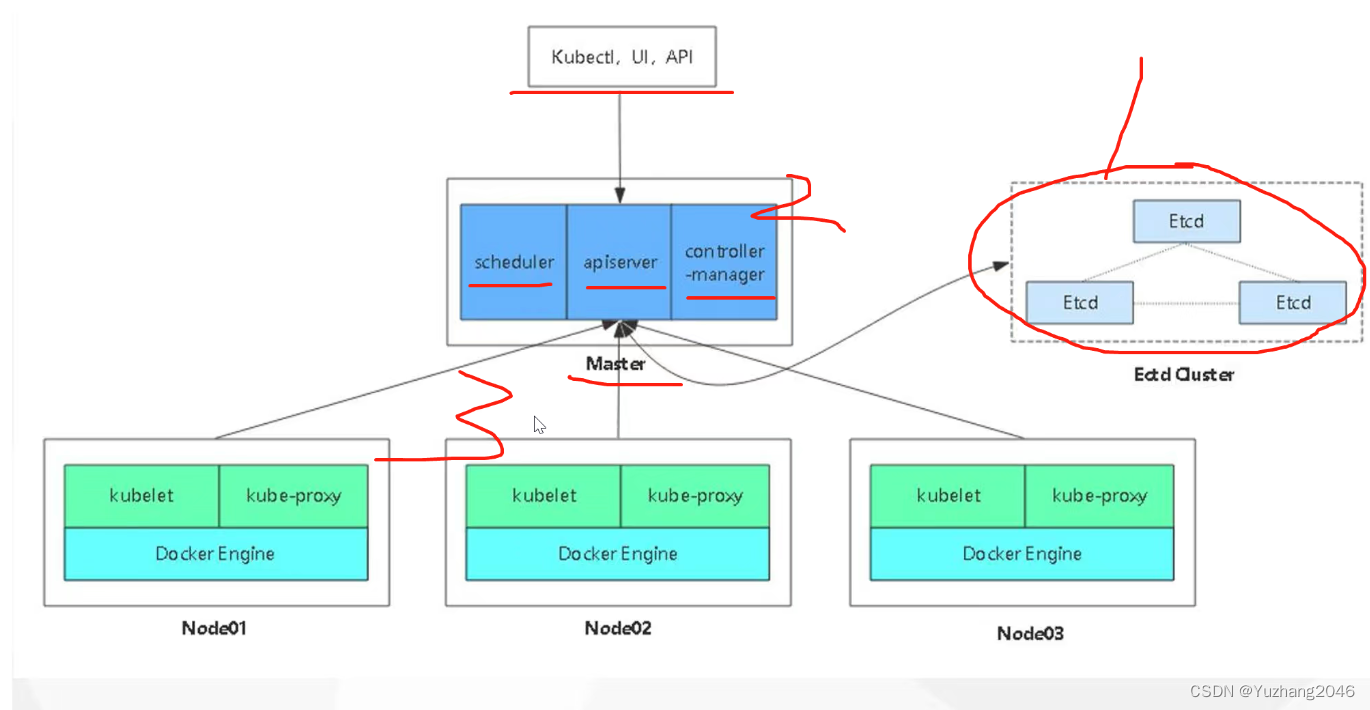
【每日一题】1595. 连通两组点的最小成本
- 1595. 连通两组点的最小成本
- 题目描述
- 解题思路
1595. 连通两组点的最小成本
题目描述
给你两组点,其中第一组中有 size1 个点,第二组中有 size2 个点,且 size1 >= size2 。
任意两点间的连接成本 cost 由大小为 size1 x size2 矩阵给出,其中 cost[i][j] 是第一组中的点 i 和第二组中的点 j 的连接成本。如果两个组中的每个点都与另一组中的一个或多个点连接,则称这两组点是连通的。换言之,第一组中的每个点必须至少与第二组中的一个点连接,且第二组中的每个点必须至少与第一组中的一个点连接。
返回连通两组点所需的最小成本。
示例 1:
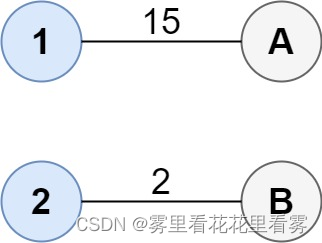
输入:cost = [[15, 96], [36, 2]]
输出:17
解释:连通两组点的最佳方法是:
1--A
2--B
总成本为 17 。
示例 2:
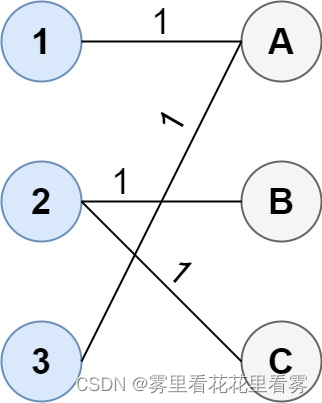
输入:cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
输出:4
解释:连通两组点的最佳方法是:
1--A
2--B
2--C
3--A
最小成本为 4 。
请注意,虽然有多个点连接到第一组中的点 2 和第二组中的点 A ,但由于题目并不限制连接点的数目,所以只需要关心最低总成本。
示例 3:
输入:cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
输出:10
提示:
size1 == cost.length
size2 == cost[i].length
1 <= size1, size2 <= 12
size1 >= size2
0 <= cost[i][j] <= 100
解题思路
思路1:贪心算法。dfs(i,j)表示在第一组的[0…i]范围内选择第二组尚未被连接的集合j的最小成本。其可以表示为第一组的i选择第二组的节点k(此处使用枚举k),然后第一组的[0…i-1]选择第二组的除去k的剩余节点的最小成本。当第一组选择完毕后,枚举第二组未被选择的节点并选择其与第一组连接的成本最小的节点(此处可以预处理)。
int connectTwoGroups(vector<vector<int>>& cost)
{
int n=cost.size();
int m=cost[0].size();
vector<int> min_cost(m,INT_MAX);
//遍历第二组节点求解各个节点和第一组节点的代价最小值
for(int j=0;j<m;j++)
{
//遍历代价数组
for(auto c:cost)
//求最小代价
min_cost[j]=min(min_cost[j],c[j]);
}
//memo[i][j]表示前i个节点中选择集合j的最小成本
vector<vector<int>> memo(n,vector<int>(1<<m,INT_MAX));
//第一组的(0,i)与第二组的j相连时的最小成本
function<int(int,int)> dfs=[&](int i,int j)->int
{
//第二组还有节点未相连则选择和第一组的代价最小的相连
if(i<0)
{
int ans=0;
for(int k=0;k<m;k++)
{
//第二组的k未相连
if((j>>k)&1)
ans+=min_cost[k];
}
return ans;
}
int &res=memo[i][j];
if(res!=INT_MAX)
return res;
for(int k=0;k<m;k++)
res=min(res,dfs(i-1,j&~(1<<k))+cost[i][k]);
return res;
};
//m个节点 0~m-1 全集
return dfs(n-1,(1<<m)-1);
}
总结:由于第一组的节点比第二组的节点多,故选择第二组的节点做掩码。记忆化搜索的本质是存在大量的重复子问题,那么我们需要分析的是重复子问题是什么?其中在剩余前i个中选择剩余状态集合j这就是一个重复的问题,故使用memo[i][j]表示在[0…i]选择j的最小成本。

![[MySQL]不允许你不会SQL语句之查询语句](https://img-blog.csdnimg.cn/1eb3d97d33b44ab691a9728de479cfb9.gif)