目录
1.0 流程图标识
1.1 语句覆盖法(C0标准)
1.2 判定/分支覆盖法(C1标准)
1.3 条件覆盖法(C2标准)
1.4 判定条件覆盖法(C1+C2标准)
1.5 条件组合覆盖法(C3标准)
1.6 路径覆盖
1.7 基本路径覆盖法
结语
1.0 流程图标识

1.1 语句覆盖法(C0标准)
① 目标
程序中的每个可执行语句至少被执行一次
后面如未说明那就是还是用的这个样例
程序源代码:
import java.util.Scanner;
public class Demo {
public static void main(String[] args) {
int a, b;
double c;
Scanner scanner = new Scanner(System.in);
a = scanner.nextInt();
b = scanner.nextInt();
c = scanner.nextDouble();
if (a > 0 && b > 0) {
c = c / a;
} else if (a > 1 || c > 1) {
c = c + 1;
}
c = b + c;
System.out.println("a=" + a);
System.out.println("b=" + b);
System.out.println("c=" + c);
scanner.close();
}
}
画出流程图:
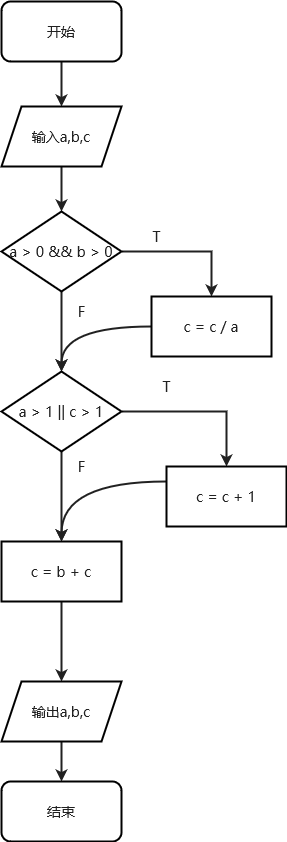
② 用例
| 输入 | 输出 |
|---|---|
| a = 2 b = 1 c = 6 | a = 2 b = 1 c = 7 |
③ 优缺点
- 语句覆盖能发现语句错误
- 语句覆盖不能发现逻辑错误
1.2 判定/分支覆盖法(C1标准)
① 目标
程序中每个判定的取真分支和取假分支至少执行一次
② 用例
| 输入 | 输出 |
|---|---|
| a = 2 b = 1 c = 6 | a = 2 b = 1 c = 5 |
| a = -1 b = 1 c = 1 | a = -1 b = 1 c = 7 |
③ 优缺点
- 判定/分支覆盖能发现逻辑错误
- 判定/分支覆盖不能发现组合判断中的条件错误
1.3 条件覆盖法(C2标准)
① 目标
程序中每个判定中每个条件的可能取值至少满足一次
② 用例
判定3:(a > 0 && b > 0)
判定6:(a > 1 || c > 1)
原子条件集:
a > 0
b > 0
a > 1
c > 1
要求:各原子条件集真假各取一次
| 输入 | 原子条件 | 判定条件 |
|---|---|---|
| a = -1 b = 2 c = 3 | a>0取假,b>0取真,a>1取假,c>1取真 | 判定3取假,判定6取真 |
| a = 2 b = -1 c = -2 | a>0取真,b>0取假,a>1取真,c>1取假 | 判定3取假,判定6取真 |
③ 优缺点
- 未必比判定/分支覆盖更全面
- 不能发现逻辑错误
1.4 判定条件覆盖法(C1+C2标准)
① 目标
每个条件中的所有可能取值至少执行一次,同时,每个判定的可能结果至少执行一次
② 用例
| 输入 | 原子条件 | 判定条件 |
|---|---|---|
| a = 2 b = 1 c = 4 | a>0取真,b>0取真,a>1取真,c>1取真 | 判定3取真,判定6取真 |
| a = -1 b = -2 c = -3 | a>0取假,b>0取假,a>1取假,c>1取假 | 判定3取假,判定6取假 |
③ 优缺点
- 可能会导致某些条件掩盖了另一些条件
1.5 条件组合覆盖法(C3标准)
① 目标
每个判定中的所有的条件取值组合至少执行一次
② 用例
判定3:(a > 0 && b > 0)
判定6:(a > 1 || c > 1)
原子条件集:
a > 0 b > 0 a > 1 c > 1
要求:
a>0时,b>0真假各一次
a<=0时,b>0真假各一次
a>1时,c>1真假各一次
a<=1时,c>1真假各一次
| 输入 | 原子条件 | 判定条件 |
|---|---|---|
| a = 2 b = 1 c = 6 | a>0取真,b>0取真,a>1取真,c>1取真 | 判定3取真,判定6取真 |
| a = 2 b = -1 c = -2 | a>0取真,b>0取假,a>1取真,c>1取假 | 判定3取假,判定6取真 |
| a = -1 b = 2 c = 3 | a>0取假,b>0取真,a>1取假,c>1取真 | 判定3取假,判定6取真 |
| a = -1 b = -2 c = -3 | a>0取假,b>0取假,a>1取假,c>1取假 | 判定3取假,判定6取假 |
③ 优缺点
- 比条件覆盖法更全面
1.6 路径覆盖
① 目标
用例覆盖程序中的所有可能的执行路径
② 用例
| 输入 | 原子条件 | 判定条件 |
|---|---|---|
| a = 2 b = 1 c = 6 | a>0取真,b>0取真,a>1取真,c>1取真 | 判定3取真,判定6取真 |
| a = 1 b = 1 c = -3 | a>0取真,b>0取真,a>1取假,c>1取假 | 判定3取真,判定6取假 |
| a = -1 b = 2 c = 3 | a>0取假,b>0取真,a>1取假,c>1取真 | 判定3取假,判定6取真 |
| a = -1 b = -2 c = -3 | a>0取假,b>0取假,a>1取假,c>1取假 | 判定3取假,判定6取假 |
③ 优缺点
- 不切实际
- 因为涉及到相关长和几乎无穷尽的路径数
- 任何可能的循环在程序段中都被视为是可能的路径
1.7 基本路径覆盖法
1)McCabe的基路径方法

2)从源节点到汇节点的线性独立路径数(根据圈复杂度计算)
- V(G) = e - n + 2p = 10 - 7 + 2 = 5
- 当规模很小时,我们可以直观地标识独立路径
3)以下给出的是用节点/边序列表示的路径:
- p1:A,B,C,G/1,4,9
- p2:A,B,C,B,C,G/1,4,3,4,9
- p3:A,B,E,F,G/1,5,8,10
- p4:A,D,E,F,G/2,6,8,10
- p5:A,D,F,G/2,7,10
以上就是这节的全部内容,如有错误,还请各位指正!
结语
这篇贴子到这里就结束了,最后,希望看这篇帖子的朋友能够有所收获。
获取方式:留言【软件测试学习】即可
如果你觉得文章还不错,请大家 点赞、分享、留言 下,因为这将是我持续输出更多优质文章的最强动力!