1. 题目

已知

(1) 世界坐标系到相机1坐标系变换关系为 $T_{(R_{1},W)}$ ，即相机1的位姿q1=[0.35,0.2,0.3,0.1]^T, t1=[0.3,0.1,0.1]^T.

(2) 世界坐标系到相机2坐标系变换关系为 $T_{(R_{2},W)}$ ，即相机2的位姿q1=[-0.5,0.4,-0.1,0.2]^T, t2=[-0.1,0.5,0.3]^T.

(3) 相机1下的某点观测坐标是 $P_{R_{1}}$

求该点在相机2坐标系下的坐标。假设该点的世界坐标是 $P_W$ ，则有

2. 使用欧式变换

世界坐标系下的坐标到相机1坐标系下的坐标变换（利用欧式变换公式）

$P_{R_{1}} = T_{(R_{1},W)} P_{W}$

世界坐标系下的坐标到相机2坐标系下的坐标变换

$P_{R_{2}} = T_{(R_{2},W)}P_{W}$

第一个公式两边左乘以T的逆，求得P_W再带入第二个公式，求得该点在相机2坐标系下的坐标

$P_{R_{2}} = T_{(R_{2},W)}T_{(R_{1},W)}^{-1}P_{R_{1}} = T_{(R_{2},W)}T_{(W,R_{1})}P_{R_{1}}$

书上的公式如下。

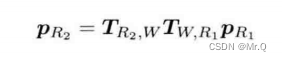
注：在SLAM中，位姿是世界坐标系到相机坐标系的变换，包括旋转与平移。

3. 使用四元素

同样，假设该点的世界坐标是 $P_W$

世界坐标系下的坐标到相机1坐标系下的坐标变换（四元素变换公式）

$P_{R_{1}} = q_{1}P_{W}q_{1}^{-1} + t_{1}$ ---------------公式1

世界坐标系下的坐标到相机2坐标系下的坐标变换

$P_{R_{2}} = q_{2}P_{W}q_{2}^{-1} + t_{2}$ ---------------公式2

变换第一个公式，两边左乘q_1逆，如下。

$q_1^{-1}P_{R_1}=P_Wq_1^{-1}+q_1^{-1}t_1$

再两边右乘q_1，如下。

$q_1^{-1}P_{R_1}q_1=P_W+q_1^{-1}t_1q_1$

P_W带入公式2中，数学公式如下。

$P_{R_2} = q_2(q_1^{-1}P_{R_1}q_1 - q_1^{-1}t_1q_1)q_2^{-1} + t_2 = q_2q_1^{-1}(P_{R_1}-t_1)q_1q_2^{-1}+t_2 = q_2q_1^{-1}(P_{R_1}-t_1)(q_2q_1^{-1})^{-1}+t_2$

eigen特点是 $qpq^{-1}$ 写成qp，即省了后面取逆操作，所以上面的公式eigen形式如下。

$P_{R_2} = q_2q_1^{-1}(P_{R_1}-t_1)+t_2$

#include <iostream>
#include <vector>
#include <algorithm>
#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Geometry>
 
using namespace std;
using namespace Eigen;
 
int main(int argc, char** argv) {
  // 已知两个相机的位姿
  // 即p1的位姿是q1 = [0.35,0.2,0.3,0.1]^T, t1 = [0.3,0.1,0.1]^T
  // 即p2的位姿是q2 = [-0.5,0.4,-0.1,0.2]^T, t2 = [-0.1,0.5,0.3]^T    
  Quaterniond q1(0.35, 0.2, 0.3, 0.1), q2(-0.5, 0.4, -0.1, 0.2);  // 旋转。coeffs的顺序是(x,y,z,w),w为实部，前三者为虚部
  q1.normalize();  // 注意，四元素使用之前需要归一化。
  q2.normalize();
  Vector3d t1(0.3, 0.1, 0.1), t2(-0.1, 0.5, 0.3);  // 平移

  // 已知p1在相机1坐标系下的坐标
  Vector3d p1(0.5, 0, 0.2);
 
  // 1, 利用四元素变换
  Vector3d p2;
  p2 = q2 * q1.inverse() * (p1 - t1) + t2;
  cout << endl << p2.transpose() << endl;
  
  // 2, 利用欧式变换矩阵
  Isometry3d T1w(q1), T2w(q2);  // 用四元素，初始化欧式变换矩阵
  T1w.pretranslate(t1);
  T2w.pretranslate(t2);
  // 求p1在相机2坐标系下的坐标
  p2 = T2w * T1w.inverse() * p1;  // 公式
  cout << endl << p2.transpose() << endl;

  return 0;
}

-0.0309731 0.73499 0.296108

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/667102.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！