一、说明
在研究双曲空间的时候,不能不遇到双曲面的问题。双曲几何在什么样的双曲面建立?其它几何元素在双曲面的表现。庞加莱盘不是双曲几何的一部分,而是一个投影平面,自然语言处理中,图网络不是卷积神经网络。本篇从双曲方程开始,展开双曲空间的探讨。
二、双曲面总论
2.1 特征和属性
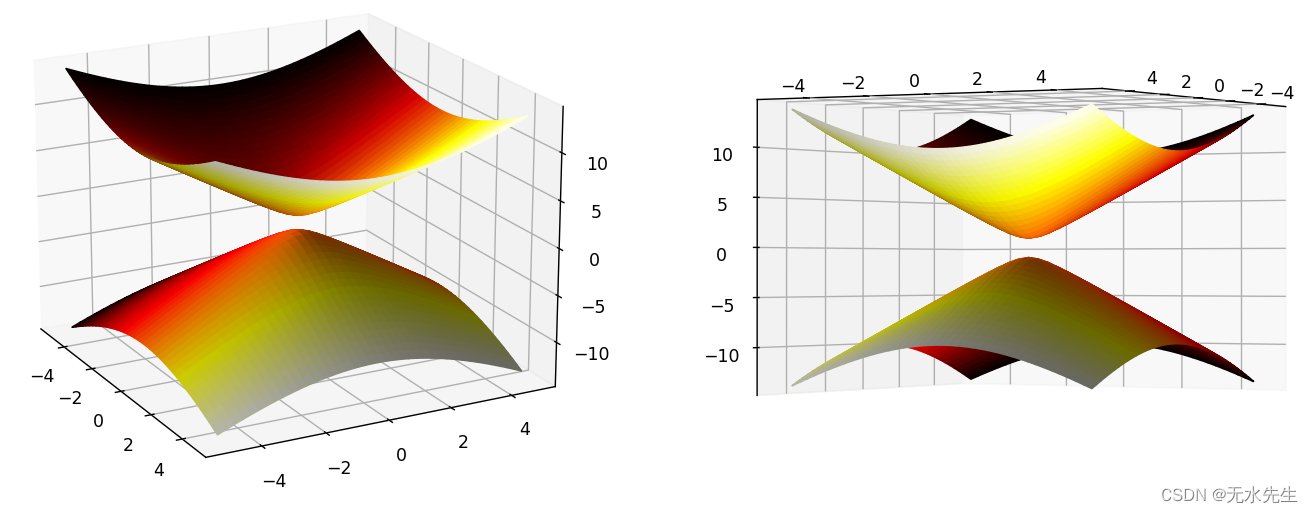
双曲面是一种曲面,其定义为与一个双曲面生成元 H(平面曲线)相交的所有切面均为双曲线。双曲面具有以下性质:
-
双曲面是一个二次曲面,可以用二次方程描述。
-
双曲面可以分为两类:单叶双曲面和双叶双曲面。单叶双曲面只有一个曲面,而双叶双曲面有两个对称的曲面。
-
双曲面的曲率比较复杂,在不同点处的曲率大小和方向都不同。它的曲率中心在参数平面上是一个双重点,对应着双曲线的两个焦点。
-
双曲面的切向量和法向量在不同点处都有不同的方向。在单叶双曲面上,切向量、法向量和曲面上的任意一点的位置向量共面;在双叶双曲面上,切向量、法向量和曲面上的任意一点的位置向量不共面。
-
双曲面具有对称性,其中包括轴对称、中心对称和面对称。这些对称性在解决一些几何问题时非常有用。
-
双曲面是一种非欧几何,与欧几里得几何和椭圆几何不同。因此,它的性质与欧几里得几何和椭圆几何有很大的区别。
2.2 单页曲面
在