第三章 散点图 scatter
参考自官方文档:https://matplotlib.org/stable/api/_as_gen/matplotlib.axes.Axes.scatter.html#matplotlib.axes.Axes.scatter
matplotblib 绘制散点图常用参数:
x, y:一个或者多个点的位置;s:标记大小(以点**2为单位)(印刷点为1/72;c:标记颜色。可选值:- 使用cmap和范数将n个数字的标量或序列映射到颜色。
- 行为RGB或RGBA的2D阵列。
- 长度为n的一系列颜色。
- 单色格式字符串。
marker:标记样式,默认"o",更多标记符号参考 https://matplotlib.org/stable/api/markers_api.html#module-matplotlib.markers。cmap:用于将标量数据映射到颜色的Colormap实例或注册的Colormap名称。norm:在使用cmap映射到颜色之前,用于将标量数据缩放到[0,1]范围的归一化方法。默认情况下,使用线性缩放,将最小值映射到0,将最大值映射到1。alpha:alpha混合值,介于0(透明)和1(不透明)之间。linewidths:线条粗细。edgecolors:边缘颜色。可选{'face', 'none', None}
3.1 官方例子
以下例子来自 matplotlib 官方
https://matplotlib.org/stable/gallery/lines_bars_and_markers/scatter_demo2.html#sphx-glr-gallery-lines-bars-and-markers-scatter-demo2-py
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cbook as cbook
# Load a numpy record array from yahoo csv data with fields date, open, high,
# low, close, volume, adj_close from the mpl-data/sample_data directory. The
# record array stores the date as an np.datetime64 with a day unit ('D') in
# the date column.
price_data = (cbook.get_sample_data('goog.npz', np_load=True)['price_data']
.view(np.recarray))
price_data = price_data[-250:] # get the most recent 250 trading days
delta1 = np.diff(price_data.adj_close) / price_data.adj_close[:-1]
# Marker size in units of points^2
volume = (15 * price_data.volume[:-2] / price_data.volume[0])**2
close = 0.003 * price_data.close[:-2] / 0.003 * price_data.open[:-2]
fig, ax = plt.subplots()
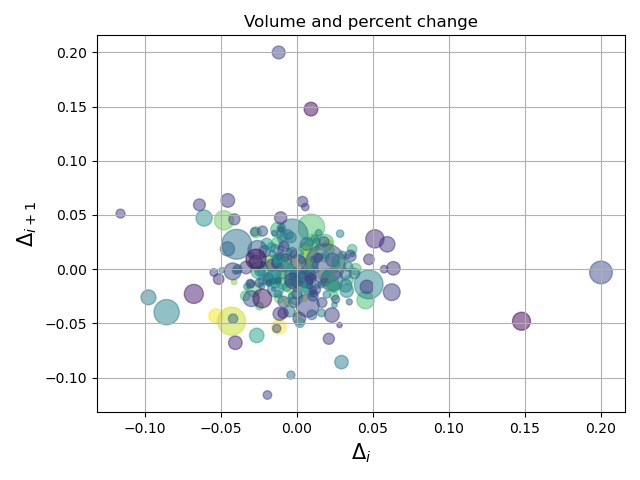
ax.scatter(delta1[:-1], delta1[1:], c=close, s=volume, alpha=0.5)
ax.set_xlabel(r'$\Delta_i$', fontsize=15)
ax.set_ylabel(r'$\Delta_{i+1}$', fontsize=15)
ax.set_title('Volume and percent change')
ax.grid(True)
fig.tight_layout()
plt.show()
绘制的效果如下:
这个例子需要注意以下几个方面:
- 官方的例子基本上都不再直接使用 plt 直接进行绘制,而是在 figure() 后返回的第二个对象进行操作;
- 并且这里提供了 latex 公式的转换功能;
- 当遇到这方面的需求,比如绘制论文实验图片,可以考虑参考这个例子。
3.2 官方例子 2
https://matplotlib.org/stable/plot_types/basic/scatter_plot.html#sphx-glr-plot-types-basic-scatter-plot-py
这个例子更加简单,代码如下:
import matplotlib.pyplot as plt
import numpy as np
plt.style.use('_mpl-gallery')
# make the data
np.random.seed(3)
x = 4 + np.random.normal(0, 2, 24)
y = 4 + np.random.normal(0, 2, len(x))
# size and color:
sizes = np.random.uniform(15, 80, len(x))
colors = np.random.uniform(15, 80, len(x))
# plot
fig, ax = plt.subplots()
ax.scatter(x, y, s=sizes, c=colors, vmin=0, vmax=100)
ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
ylim=(0, 8), yticks=np.arange(1, 8))
plt.show()
绘制效果如下:

3.3 线性回归例子
import matplotlib.pyplot as plt
import numpy as np
# Fixing random state for reproducibility
np.random.seed(19680801)
x = np.arange(0.0, 50.0, 2.0)
y = x ** 2 + np.random.rand(*x.shape) * 30.0
sizes = np.random.rand(*x.shape) * 800 + 500
fig, ax = plt.subplots()
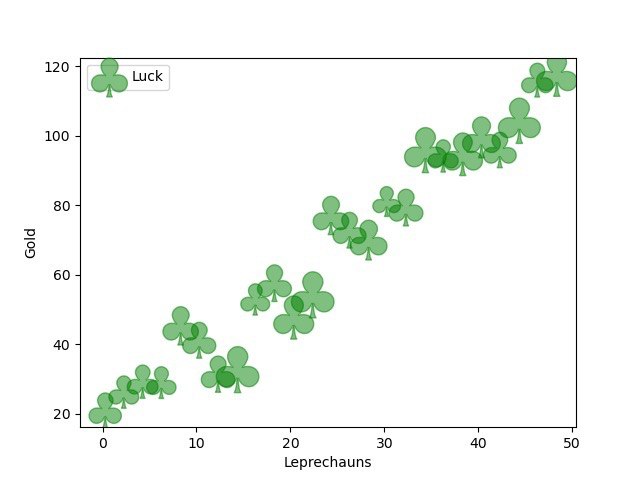
ax.scatter(x, y, sizes, c="green", alpha=0.5, marker=r'$\clubsuit$',
label="Luck")
ax.set_xlabel("Leprechauns")
ax.set_ylabel("Gold")
ax.legend()
plt.show()
绘制结果为:
3.4 多类型散点图
这里以三类散点图为例
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(19680801)
fig, ax = plt.subplots()
for color in ['tab:blue', 'tab:orange', 'tab:green']:
n = 50
x, y = np.random.rand(2, n)
scale = 200.0 * np.random.rand(n)
ax.scatter(x, y, c=color, s=scale, label=color,
alpha=0.3, edgecolors='none')
ax.legend()
ax.grid(True)
plt.show()
绘制结果为:
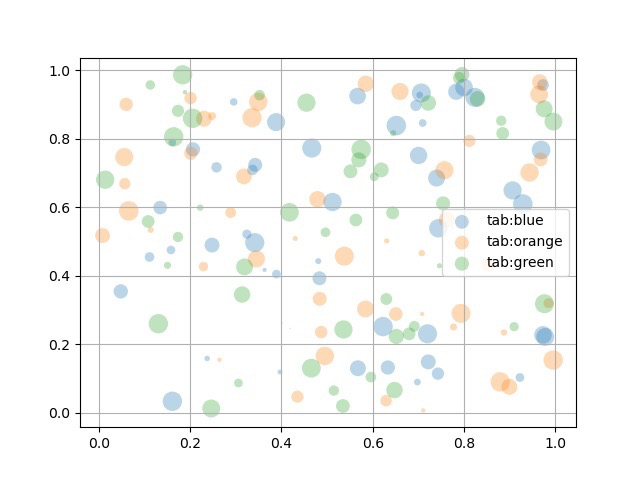
3.5 极轴上的散点图
摘录自 https://matplotlib.org/stable/gallery/pie_and_polar_charts/polar_scatter.html#sphx-glr-gallery-pie-and-polar-charts-polar-scatter-py
import numpy as np
import matplotlib.pyplot as plt
# Fixing random state for reproducibility
np.random.seed(19680801)
# Compute areas and colors
N = 150
r = 2 * np.random.rand(N)
theta = 2 * np.pi * np.random.rand(N)
area = 200 * r**2
colors = theta
fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)
plt.show()
绘制效果如下:
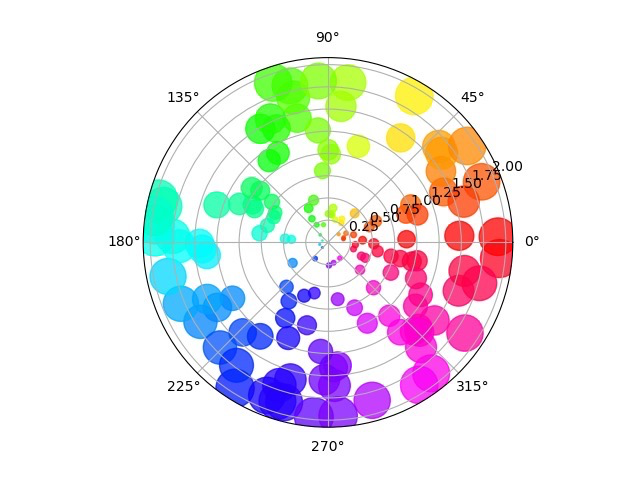
类似图片的绘制推荐参考官网地址:https://matplotlib.org/stable/gallery/pie_and_polar_charts/polar_scatter.html#sphx-glr-gallery-pie-and-polar-charts-polar-scatter-py


3.6 三维散点图
import matplotlib.pyplot as plt
import numpy as np
# Fixing random state for reproducibility
np.random.seed(19680801)
def randrange(n, vmin, vmax):
"""
Helper function to make an array of random numbers having shape (n, )
with each number distributed Uniform(vmin, vmax).
"""
return (vmax - vmin)*np.random.rand(n) + vmin
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
n = 100
# For each set of style and range settings, plot n random points in the box
# defined by x in [23, 32], y in [0, 100], z in [zlow, zhigh].
for m, zlow, zhigh in [('o', -50, -25), ('^', -30, -5)]:
xs = randrange(n, 23, 32)
ys = randrange(n, 0, 100)
zs = randrange(n, zlow, zhigh)
ax.scatter(xs, ys, zs, marker=m)
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()
绘制效果如下:
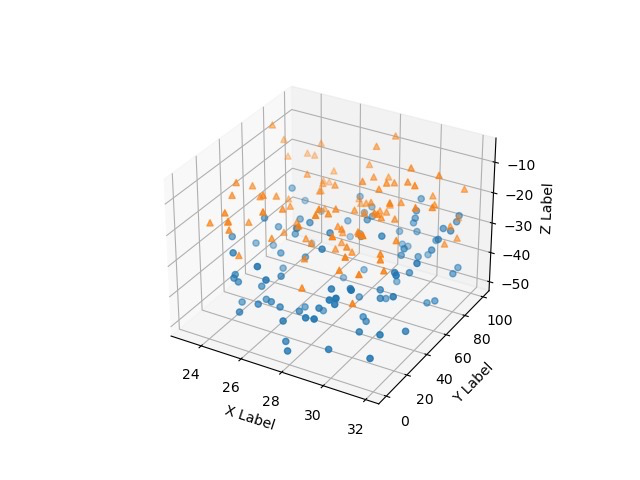
3.7 本章总结
绘制自己需要的散点图的步骤大致如下:
- 明确自己需要绘制的散点图类型;
- 确保待绘制图片的数据没有问题;
- 复制类似的例子源码,根据参数说明修改参数,绘制符合个性化需求的图片。
Smileyan
2022.12.6 22:00

![[附源码]Python计算机毕业设计SSM家政服务预约小程序(程序+LW)](https://img-blog.csdnimg.cn/5d3e9784834a4eaeba30ca32319d9b7f.png)

![[附源码]Python计算机毕业设计SSM家政服务管理系统(程序+LW)](https://img-blog.csdnimg.cn/a5de3acc78724b419b883fc911247342.png)

![[附源码]计算机毕业设计基于Springboot作业管理系统](https://img-blog.csdnimg.cn/52750c3984674a9191c2d83513a06fd7.png)




![[附源码]Python计算机毕业设计Django物品捎带系统](https://img-blog.csdnimg.cn/be555bd9512949f69022449c0c5939d6.png)