一、介绍
手写数字识别系统,使用Python语言,基于TensorFlow搭建CNN卷积神经网络算法对数据集进行训练,最后得到模型,并基于FLask搭建网页端界面,基于Pyqt5搭建桌面端可视化界面。
二、效果展示
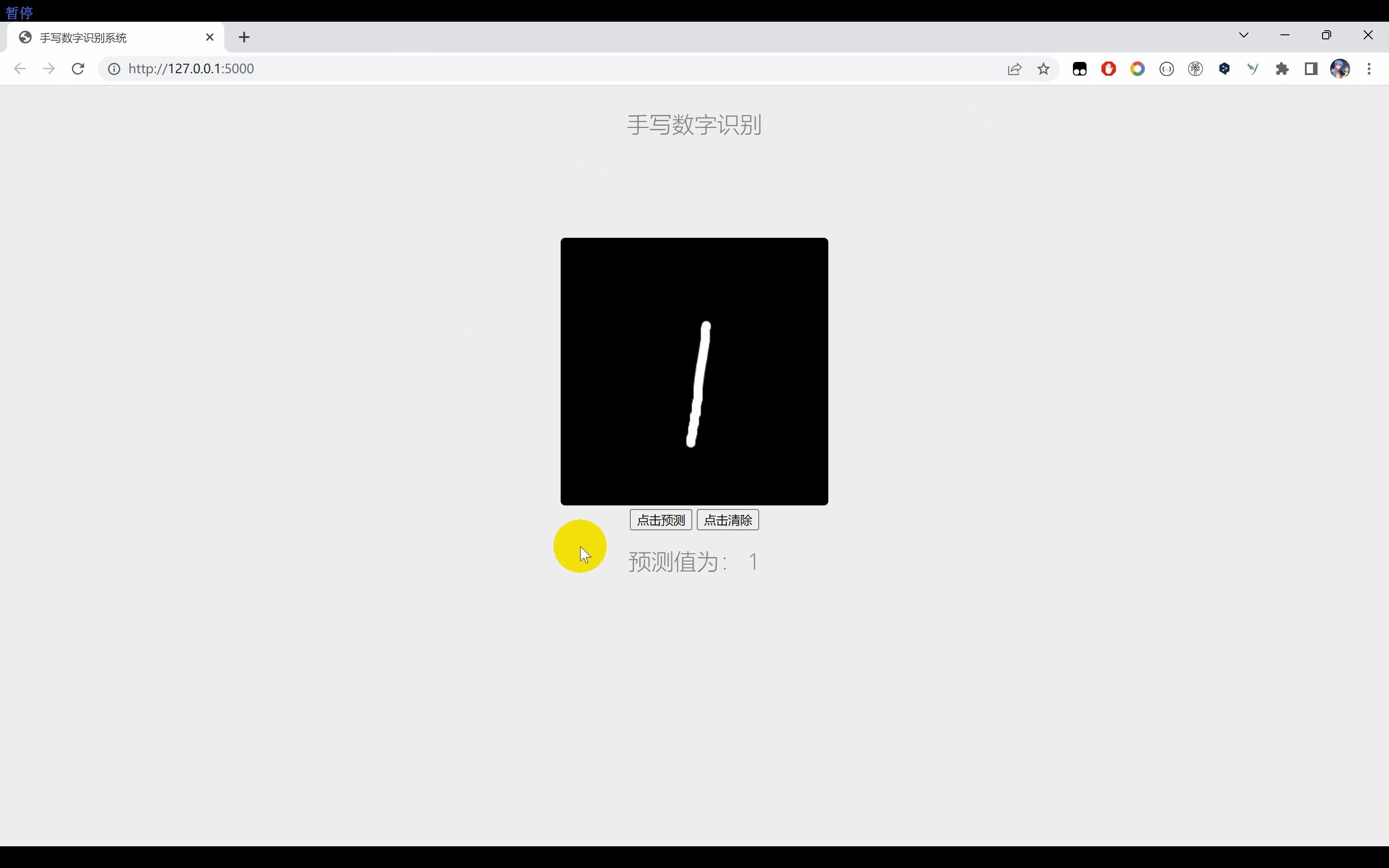
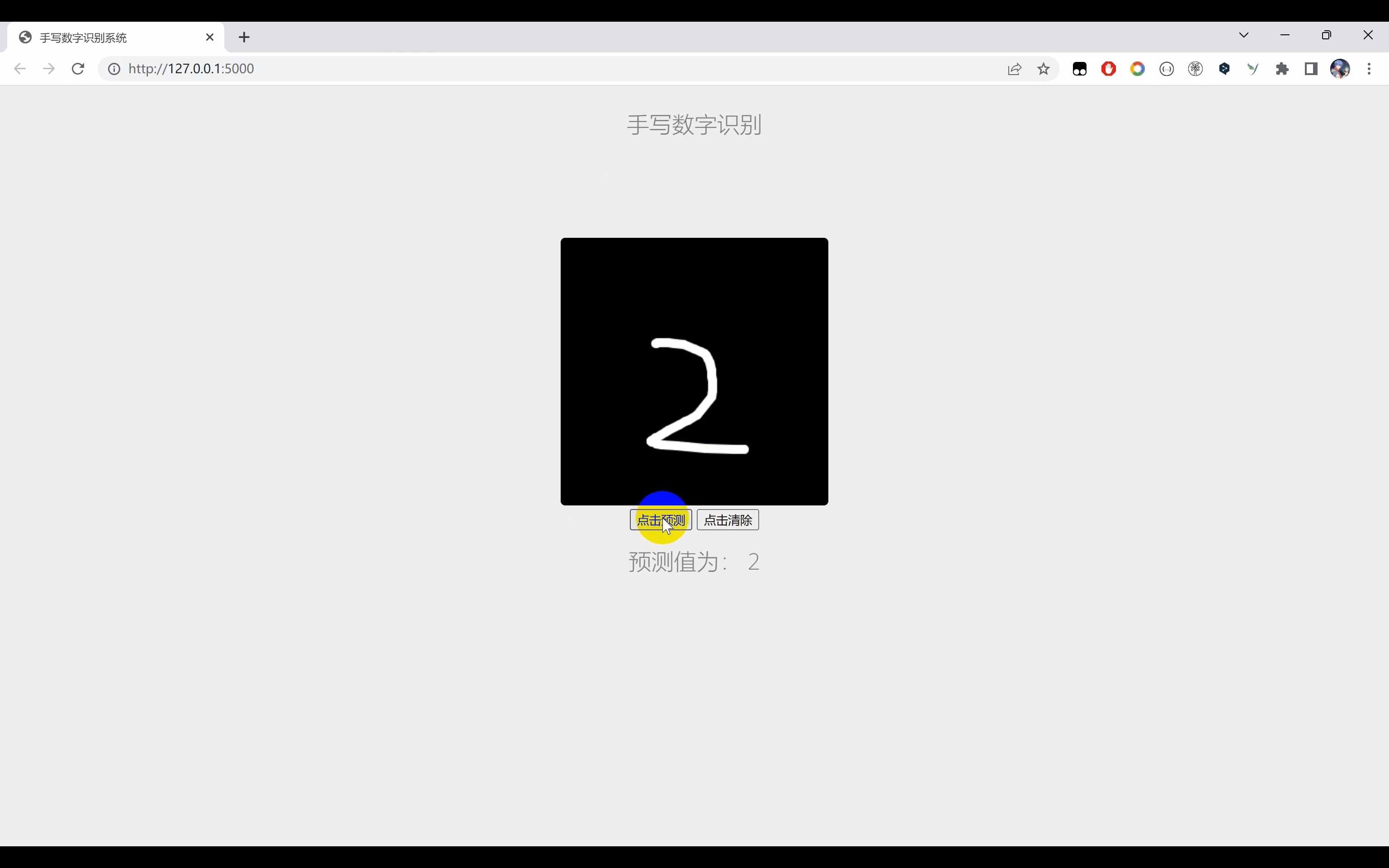
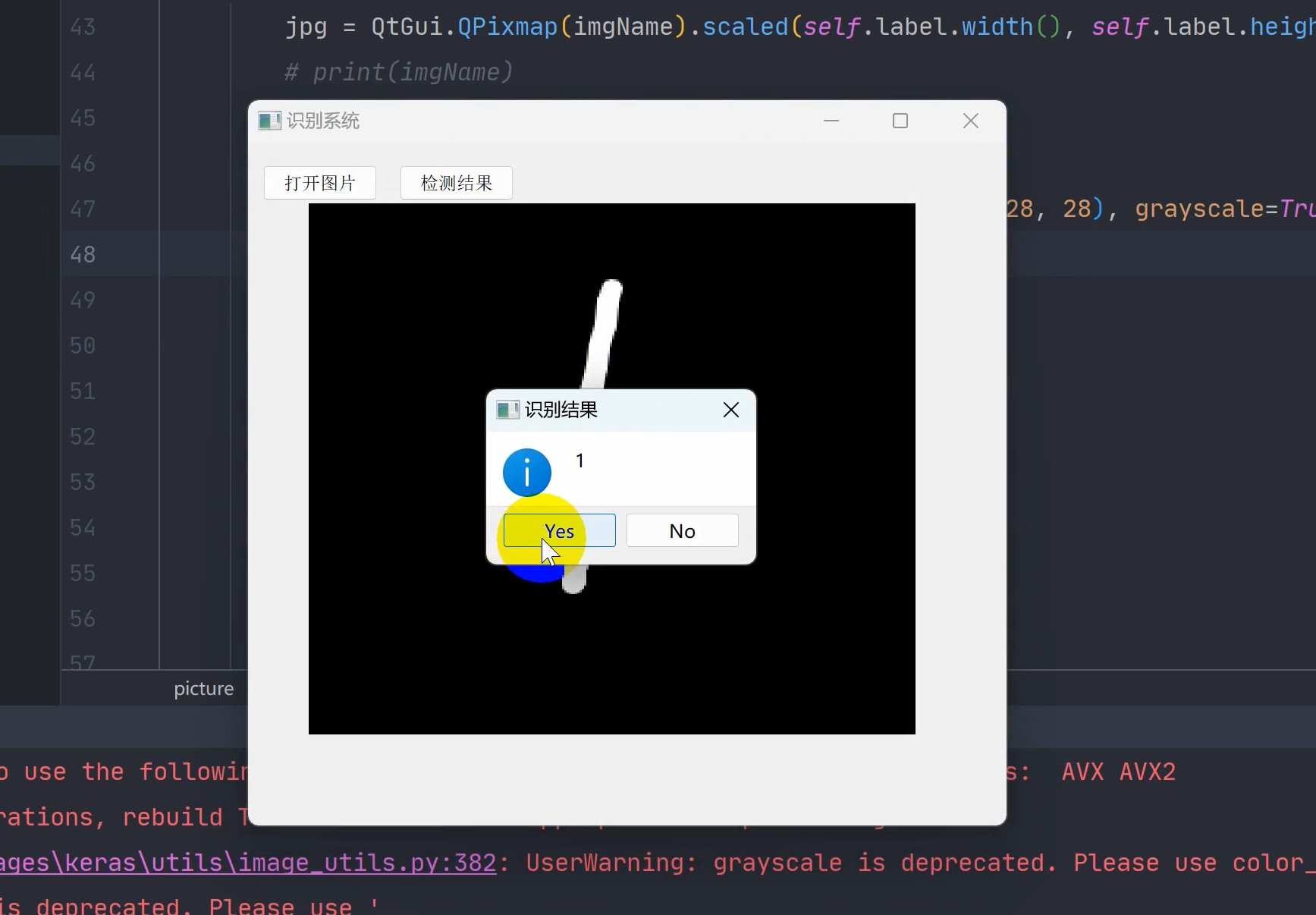
三、演示视频+完整代码
视频+代码:https://www.yuque.com/ziwu/yygu3z/tb1mzqi847daqkru
四、手写数字识别
当涉及手写数字识别系统时,TensorFlow是一个强大的工具,它提供了许多用于构建深度学习模型的功能。以下是一个基本的代码示例,展示了如何使用TensorFlow来构建、训练和测试手写数字识别系统。
首先,我们需要导入所需的库和模块:
pythonCopy codeimport tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
接下来,我们可以加载并预处理手写数字数据集(例如MNIST数据集):
pythonCopy code# 加载MNIST数据集
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
# 将像素值缩放到0到1之间
x_train = x_train.astype("float32") / 255.0
x_test = x_test.astype("float32") / 255.0
# 将标签转换为独热编码(one-hot encoding)
y_train = keras.utils.to_categorical(y_train)
y_test = keras.utils.to_categorical(y_test)
接下来,我们可以定义一个基本的卷积神经网络(CNN)模型来进行手写数字识别:
pythonCopy codemodel = keras.Sequential([
layers.Reshape(target_shape=(28, 28, 1), input_shape=(28, 28)),
layers.Conv2D(filters=32, kernel_size=(3, 3), activation='relu'),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.Flatten(),
layers.Dense(units=128, activation='relu'),
layers.Dense(units=10, activation='softmax')
])
现在,我们可以编译模型并开始训练:
pythonCopy codemodel.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
model.fit(x_train, y_train, batch_size=128, epochs=5, validation_data=(x_test, y_test))
在训练过程中,我们使用Adam优化器和交叉熵损失函数。我们还指定了每个批次的大小(128)和训练周期的数量(5)。通过使用验证集(x_test和y_test)进行验证,我们可以评估模型的性能。
训练完成后,我们可以使用测试集来评估模型的准确性:
pythonCopy codetest_loss, test_acc = model.evaluate(x_test, y_test)
print("Test accuracy:", test_acc)
以上代码提供了一个基本的手写数字识别系统的构建、训练和测试流程。你可以根据需要对模型进行调整和优化,例如增加网络的深度、调整超参数等,以提高准确性。
五、CNN卷积神经网络
卷积神经网络(Convolutional Neural Network,CNN)是一种用于处理具有网格结构数据的深度学习模型。它在计算机视觉任务中取得了显著的成功,特别是在图像分类、目标检测和图像分割等领域。
CNN的核心思想是通过卷积层、池化层和全连接层等组件来提取和学习图像特征,从而实现高效的图像识别和处理。下面是CNN的一些重要组件和特性:
- 卷积层(Convolutional layers):卷积层是CNN的核心组件,它通过应用一系列的滤波器(也称为卷积核)对输入数据进行卷积操作,从而提取图像中的局部特征。卷积操作通过滑动滤波器窗口在输入数据上进行元素级乘法和求和运算。卷积层可以学习到不同的滤波器,从而捕捉到图像的不同特征,如边缘、纹理和形状等。
- 池化层(Pooling layers):池化层用于减小特征图的空间尺寸,并减少模型中的参数数量。常用的池化操作包括最大池化和平均池化,它们通过在局部区域内选择最大或平均值来减小特征图的尺寸。池化层有助于增强模型的平移不变性,并提取出更加鲁棒的特征。
- 激活函数(Activation functions):在卷积层和全连接层之间,激活函数被应用于每个神经元的输出,引入非线性性质。常用的激活函数包括ReLU(Rectified Linear Unit)、sigmoid和tanh等。ReLU是最常用的激活函数,它在正区间上直接输出输入值,并在负区间上输出零,具有较好的收敛性和计算效率。
- 全连接层(Fully connected layers):在CNN的最后几层,可以使用全连接层来进行分类和预测。全连接层将前一层的所有神经元与当前层的每个神经元相连,通过学习权重来建立输入和输出之间的关系。全连接层通常用于将提取的特征映射转换为最终的预测结果。