1.简述

      随着数据量的不断增加和数据维度的不断扩展，如何进行高效的数据降维处理成为了一个热门话题。在数据分析领域，PCA算法作为一种常用的数据降维方法，可以对多个特征进行降维，提高计算效率和降低存储空间需求。本文以波士顿房价数据集为例，探讨如何利用PCA算法对房屋价格进行降维。

什么是主成分分析？

​ PCA（Principal Component Analysis） 是一种常见的数据分析方式，常用于高维数据的降维，可用于提取数据的主要特征分量。PCA通常用于降低大型数据集的维数，方法是数据集中的指标数量变少，并且保留原数据集中指标的大部分信息。总而言之：减少数据指标数量，保留尽可能多的信息。

PCA适用范围

• 在已标注与未标注的数据上都有降维技术
• 主要关注未标注数据上的降维技术，将技术同样也可以应用于已标注的数据。

优缺点

​ PCA优点在于数据降维，便于提取数据的主要特征，使得数据更容易使用，减少计算开销，去除噪音等等。缺点在于不一定需要，有可能损失有用信息，只针对训练集保留主要信息，可能造成过拟合。适用于结构化数据.PCA不仅能将数据压缩，也使得降维之后的数据特征相互独立。

PCA的方法步骤

​ PCA作为一个传统的机器学习算法，可以通过基础的线代知识推导（协方差矩阵计算，计算特征向量，特征值，正交...）。主要涉及的数学方法不在本节过多描述，有兴趣的读者可以参考花书中的线性代数部分，做推导。PCA的步骤主要分为五步；

 标准化连续初始变量的范围（非结构化转成结构化）

​ 此步骤的目的是标准化结构化指标的范围，因为PCA对于初始变量的方差非常敏感，如果初始变量的范围之间存在较大差异，则会造成很大变差，使用标准化可以将数据转换为可比较的尺度。

2.代码

%% I. 清空环境变量   主成分分析
clear all
clc

%% II. 导入数据
load spectra;

%% III. 随机划分训练集与测试集
temp = randperm(size(NIR, 1));
% temp = 1:60;
%%
% 1. 训练集——50个样本
P_train = NIR(temp(1:50),:);
T_train = octane(temp(1:50),:);
%%
% 2. 测试集——10个样本
P_test = NIR(temp(51:end),:);
T_test = octane(temp(51:end),:);

%% IV. 主成分分析
%%
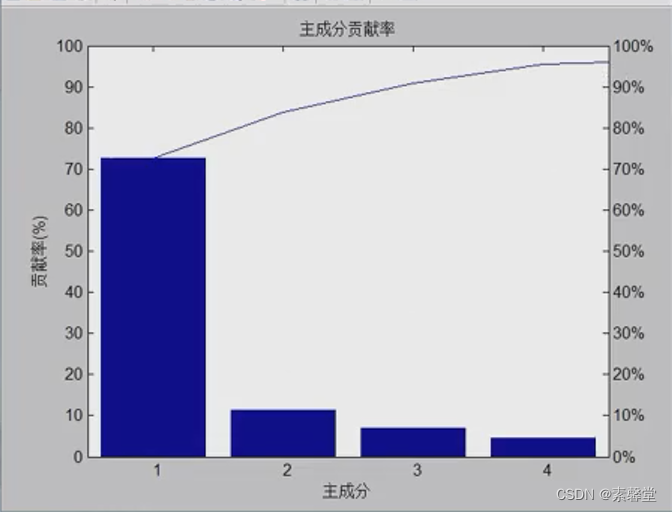
% 1. 主成分贡献率分析     PCAVar   特征值
[PCALoadings,PCAScores,PCAVar] = princomp(NIR);
figure
percent_explained = 100 * PCAVar / sum(PCAVar);
pareto(percent_explained)
xlabel('主成分')
ylabel('贡献率(%)')
title('主成分贡献率')

%%
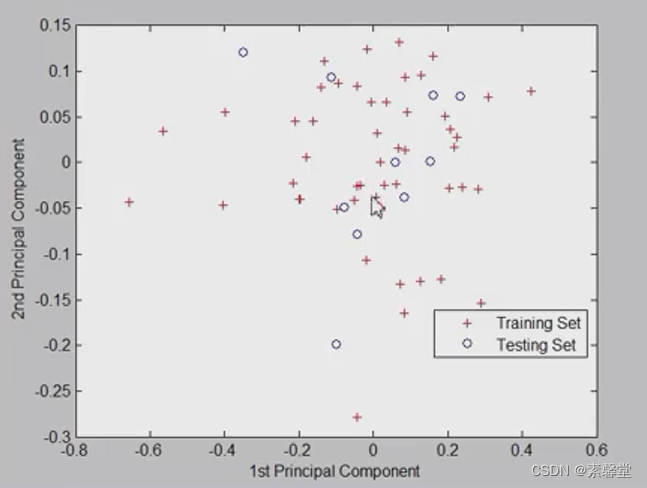
% 2. 第一主成分vs.第二主成分   可以用于训练样本是否好的判断依据
[PCALoadings,PCAScores,PCAVar] = princomp(P_train);
figure
plot(PCAScores(:,1),PCAScores(:,2),'r+')
hold on
[PCALoadings_test,PCAScores_test,PCAVar_test] = princomp(P_test);
plot(PCAScores_test(:,1),PCAScores_test(:,2),'o')
xlabel('1st Principal Component')
ylabel('2nd Principal Component')
legend('Training Set','Testing Set','location','best')

%% V. 主成分回归模型
%%
% 1. 创建模型
k = 4;    %主成分设置为4个
betaPCR = regress(T_train-mean(T_train),PCAScores(:,1:k));    %前四列提取出来建立回归模型
betaPCR = PCALoadings(:,1:k) * betaPCR;
betaPCR = [mean(T_train)-mean(P_train) * betaPCR;betaPCR];
%%
% 2. 预测拟合
N = size(P_test,1);       %大家根据自己情况调整N值和P_test
T_sim = [ones(N,1) P_test] * betaPCR;         

%% VI. 结果分析与绘图
%%
% 1. 相对误差error
error = abs(T_sim - T_test) ./ T_test;
%%
% 2. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2)); 
%%
% 3. 结果对比
result = [T_test T_sim error]

%% 
% 4. 绘图
figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值','location','best')
xlabel('预测样本')
ylabel('辛烷值')
string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};
title(string)

 

3.运行结果