目录
前言
希尔排序
发展历史
基本思想
时间复杂度
🥰我们以一组数字来说操作说明:
gap的选取
动图演示
代码:
总结:
前言
🥰在学数据结构的第一节课就知道了数据结构课程是要管理并且学会操作数据,当然操作数据首先想到的就是数据的排序,排过顺序的数据的使用价值才够大。前面我们学习了顺序表也学习了链表等等,这些就是储存数据的方法,下面我们来看一看希尔排序的特点与效率怎么样。😍
🚩希尔排序是对直接插入排序的优化,在学习之前,没有学过插入排序的大佬们建议先学习插入排序:点这里跳转到插入排序🥰
希尔排序
🍟希尔排序(Shell's Sort)是插入排序(插入排序-C语言实现_硕硕C语言的博客-CSDN博客)的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。
⭕中文名 :希尔排序 ⭕外文名:Shell's Sort
⭕别 名:缩小增量排序 ⭕类 型:插入排序
⭕空间复杂度:O(1) ⭕稳定性:不稳定
发展历史
🍟希尔排序按其设计者希尔(Donald Shell)的名字命名,该算法由希尔在 1959 年所发表的论文“A high-speed sorting procedure” 中所描述。希尔排序是基于插入排序的以下两点性质而提出改进方法的:
⭕插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。但插⭕入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
🍟1961年,IBM 公司的女程序员 Marlene Metzner Norton(玛琳·梅茨纳·诺顿)首次使用FORTRAN语言编程实现了希尔排序算法。在其程序中使用了一种简易有效的方法设置希尔排序所需的增量序列:第一个增量取待排序记录个数的一半,然后逐次减半,最后一个增量为 1。
🍟该算法后来被称为 Shell-Metzner 算法 ,Metzner 本人在2003年的一封电子邮件中说道:“我没有为这种算法做任何事,我的名字不应该出现在算法的名字中。”
基本思想
🚩希尔排序是对插入排序的优化,基本思路是先选定一个整数作为增量,把待排序文件中的所有数据分组,以每个距离的等差数列为一组,对每一组进行排序,然后将增量缩小,继续分组排序,重复上述动作,直到增量缩小为1时,排序完正好有序。
🚩希尔排序原理是每一对分组进行排序后,整个数据就会更接近有序,当增量缩小为1时,就是插入排序,但是现在的数组非常接近有序,移动的数据很少,所以效率非常高,所以希尔排序又叫:缩小增量排序。
🚨每次排序让数组接近有序的过程叫做预排序,最后一次插入是直接插入排序
时间复杂度
🍪希尔排序的时间的时间复杂度为:O( ),希尔排序时间复杂度的下界是n*log2n。
🥝希尔排序没有快速排序算法快 O(n(logn)),因此中等大小规模表现良好,对规模非常大的数据排序不是最优选择。但是比O()复杂度的算法快得多。并且希尔排序非常容易实现,算法代码短而简单。
🍔Shell算法的性能与所选取的分组长度序列有很大关系。只对特定的待排序记录序列,可以准确地估算关键词的比较次数和对象移动次数。想要弄清关键词比较次数和记录移动次数与增量选择之间的关系,并给出完整的数学分析,今仍然是数学难题。
🥰具体我们以一组数字来说操作说明:
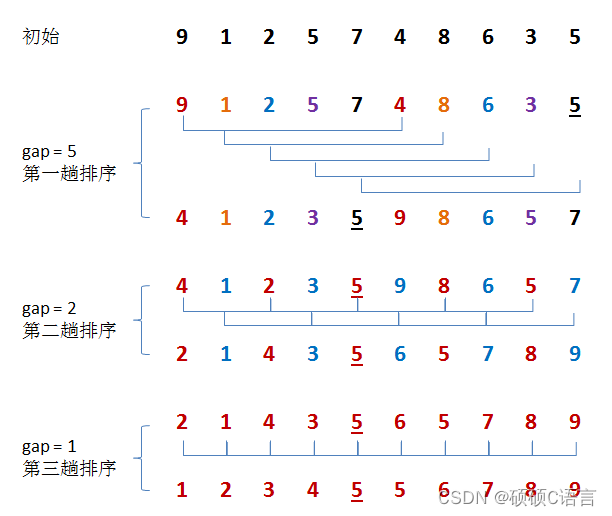
🔴 假设有一组{9, 1, 2, 5, 7, 4, 8, 6, 3, 5}无需序列。
⭕第一趟排序:
🥝设 gap1 = N / 2 = 5,即相隔距离为 5 的元素组成一组,可以分为 5 组。接下来,按照直接插入排序的方法对每个组进行排序。
⭕第二趟排序:
🥝将上次的 gap 缩小一半,即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组,可以分为2组。按照直接插入排序的方法对每个组进行排序。
⭕第三趟排序:
🥝再次把 gap 缩小一半,即gap3 = gap2 / 2 = 1。 这样相隔距离为1的元素组成一组,即只有一组。按照直接插入排序的方法对每个组进行排序。此时,排序已经结束。🚨注:需要注意一下的是,图中有两个相等数值的元素5和5。我们可以清楚的看到,在排序过程中,两个元素位置交换了。
gap的选取
🍁希尔排序的效率取决于增量值gap的选取,时间复杂度并不是一个定值。开始时,gap取值较大,子序列中的元素较少,排序速度快,克服了直接插入排序的缺点;其次,gap值逐渐变小后,虽然子序列的元素逐渐变多,但大多元素已基本有序,所以继承了直接插入排序的优点,能以近线性的速度排好序。
🍁步长的选择是希尔排序的重要部分,只要最终步长为1任何步长序列都可以工作。算法最开始以一定的步长进行排序,然后会继续以一定步长进行排序,最终算法以步长为1进行排序。当步长为1时,算法变为插入排序,这就保证了数据一定会被排序。
🍁最初的建议是折半再折半知道最后的步长为1<也就是插入排序>,虽然这样取可以比O(n2)类的算法(插入排序)更好,但这样仍然有减少平均时间和最差时间的余地。可能希尔排序最重要的地方在于当用较小步长排序后,以前用的较大步长仍然是有序的。比如, 如果一个数列以步长5进行了排序然后再以步长3进行排序,那么该数列不仅是以步长3有序,而且是以步长5有序。如果不是这样,那么算法在迭代过程中会打乱以前的顺序,那就不会以如此短的时间完成排序了。
🍁最优的空间复杂度为开始元素已排序,则空间复杂度为 0;最差的空间复杂度为开始元素为逆排序,则空间复杂度为 O(N);平均的空间复杂度为O(1)希尔排序并不只是相邻元素的比较,有许多跳跃式的比较,难免会出现相同元素之间的相对位置发生变化。比如上面的例子中希尔排序中相等数据5就交换了位置,所以希尔排序是不稳定的算法。
动图演示
代码:
//希尔排序
void ShellSort(int a[], int n)
{
// 1、gap > 1 预排序
// 2、gap == 1 直接插入排序
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1; // +1可以保证最后一次一定是1
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}总结:
🍎希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能,交换不相邻的元素以对数组的局部进行排序,最终用插入排序将局部有序的数组排序。
🍎希尔排序时效分析很难,关键码的比较次数与记录移动次数依赖于增量因子序列d的选取,特定情况下可以准确估算出关键码的比较次数和记录的移动次数。目前还没有人给出选取最好的增量因子序列的方法。增量因子序列可以有各种取法,有取奇数的,也有取质数的,但需要注意:因子中除1外增量没有公因子,且最后一个增量因子必须为1。
🍟后面硕硕也会整理一些快速排序,以及更快的排序方法,谢谢大家的观看。如果发现硕硕有什么错误的地方欢迎到评论区留言。一起加油吧🥰🥰🥰