代码随想录刷题记录day36 整数拆分+不同的二叉搜索树

参考：代码随想录

343. 整数拆分

思想

一个数可以被拆分成2个数或者3个及以上的数。

dp[i]表示拆分i以后，得到的最大的乘积

拆分成两个数 j和i-j,拆分成三个数及以上 j 和dp[i-j]，dp[i-j]表示继续拆分i-j 得到的最大的成绩

那么只要遍历j，就能把所有的拆分情况都给包含进来。

在某一轮遍历中

dp[i]=max(i*(i-j),j*dp[i-j])

由于j是遍历了每一种情况，所以dp[i]还是要取最大值的

代码

public int integerBreak(int n) {
        //dp[i]: 表示把i拆分得到的最大的乘积
        //dp[i] 可以从两个方向计算而来
        // 1. 遍历j dp【i】=j*dp【i-j】 把i拆分成2个以上
        //2.   遍历j dp【i】=j*（i-j） 就把i拆分成两个
        //dp[i]=max(dp【i】=j*dp【i-j】,dp【i】=j*（i-j）)

        //所以递推公式：dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
        //
        //那么在取最大值的时候，为什么还要比较dp[i]呢？
        //
        //因为在递推公式推导的过程中，每次计算dp[i]，取最大的而已。>>>>>???????
        //还要再取一次max  因为j是循环了  j取一个值 只是得到了dp【i】的一种可能

        int[] dp=new int[n+1];
        dp[2]=1;//把2 拆分的最大乘积是1

        //todo 遍历顺序
        //确定遍历顺序，先来看看递归公式：dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
        //
        //dp[i] 是依靠 dp[i - j]的状态，所以遍历i一定是从前向后遍历，先有dp[i - j]再有dp[i]。
        //
        //枚举j的时候，是从1开始的。i是从3开始，这样dp[i - j]就是dp[2]正好可以通过我们初始化的数值求出来。
        //
        //所以遍历顺序为：
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j < i-1; j++) {
                dp[i]=Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j]));
            }
        }
        return dp[n];
    }

96. 不同的二叉搜索树

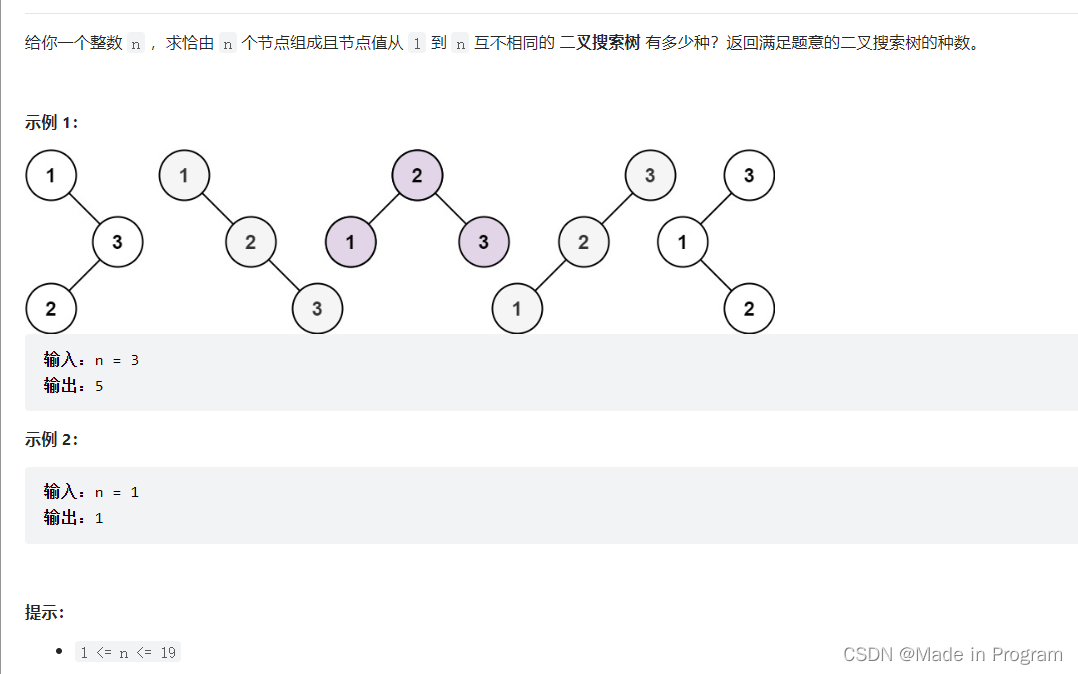
思想

1.dp[i]的含义，表示以1到i为头节点的个数，或者说有i个元素的二叉搜索树的数量

dp[3]=以1为头节点的数量+以2为头节点的数量+以3为头节点的数量

以1为头节点的数量=右子树2个元素的搜索树的数量*左子树0个元素的搜索树的数量=dp[2]*dp[0]

以2为头节点的数量=右子树1个元素的搜索树的数量*左子树1个元素的搜索树的数量=dp[1]*dp[1]

以3为头节点的数量=右子树0个元素的搜索树的数量*左子树2个元素的搜索树的数量=dp[0]*dp[2]

2.递推公式

dp[i]+=dp[i-j]*dp[j-1],其中j从1开始遍历，以j为头节点，那么左子树的节点数量就有j-1个，右子树的节点数量有i-j个

比如i=3，j=1时，左子树0个节点，右子树2个节点

3.初始化

0个节点也算是一种情况，dp[0]=1

4.遍历顺序

节点数为i的状态是依靠i之前的节点数的状态的，所以从前往后遍历

代码

class Solution {
    public int numTrees(int n) {
        //1.dp[i]的含义，表示以1到i为头节点的个数，或者说有i个元素的二叉搜索树的数量
        //dp[3]=以1为头节点的数量+以2为头节点的数量+以3为头节点的数量
        //以1为头节点的数量=右子树2个元素的搜索树的数量*左子树0个元素的搜索树的数量=dp[2]*dp[0]
        //以2为头节点的数量=右子树1个元素的搜索树的数量*左子树1个元素的搜索树的数量=dp[1]*dp[1]
        //以3为头节点的数量=右子树0个元素的搜索树的数量*左子树2个元素的搜索树的数量=dp[0]*dp[2]

        //递推公式 
        //dp[i]+=dp[i-j]*dp[j-1],其中j从1开始遍历，以j为头节点，那么左子树的节点数量就有j-1个，右子树的节点数量有i-j个
        //比如i=3，j=1时，左子树0个节点，右子树2个节点

        int [] dp=new int[n+1];
        //初始化
        dp[0]=1;

        for(int i=1;i<=n;i++){
            for(int j=1;j<=i;j++){
                dp[i]+=dp[i-j]*dp[j-1];
            }
            //System.out.println(dp[i]);
        }

        return dp[n];
    }
}