本次习题所用到的数据,#数据集:ex3data1.mat,参数:ex3weights.mat。在文章开头,下载即可!
逻辑回归解决多分类问题
二分类VS多分类
在机器学习中,分类是一种监督学习任务,其中我们试图预测目标变量的离散值。二分类和多分类是分类问题中两种最常见的形式。
-
二分类问题:
二分类问题是指需要从两个互斥的类别中选择一个类别的问题。也就是说最终的数据的标签只有两个分类,非此即彼。例如- 将电子邮件分类为垃圾邮件或非垃圾邮件
- 将患者分类为患有某种疾病或没有患该疾病等都属于二分类问题。
在二分类问题中,通常使用逻辑回归、支持向量机(SVM)和决策树等模型进行建模。
-
多分类问题:
多分类问题是指需要从多个类别中选择一个类别的问题。例如- 将一张图片分类为苹果、梨子、香蕉或橙子
- 手写数字识别0-9等都属于多分类问题。
在多分类问题中,通常使用softmax回归、决策树等模型进行建模。在深度学习中,常用的多分类算法包括卷积神经网络(CNN)、循环神经网络(RNN)等。
需要注意的是,在二分类问题中,可以使用多种方法来与该问题等效地处理多分类问题。例如,通过对多个二分类模型输出的概率进行组合,可以得到多分类模型。在本质上,多分类问题是二分类问题的一种特殊情况。
作业案例内容
案例:手写数字识别 0-9
注意:提供的原始数据中,y的取值为1-10,y=10表示当前数字为0
案例数据 ex3data1.mat
matlab的一种数据格式。MATLAB是一种数值计算引擎和编程语言,被广泛用于科学计算、工程和技术领域。MATLAB可以读取和处理各种数据格式,其中 .mat 是常见的一种格式。.mat 文件是一种二进制文件格式,可以存储多种类型的数据,包括数值、字符、逻辑和结构体等。
由于我们要处理的案例是10分类问题,使用逻辑回归来解决,处理这些数据,需要建立10个分类器,每个分类器需要判别当前这个数据的内容是否属于其中的一个类别,例如分类器1用来判断为数字1的概率,以此类推

一些用到的知识点
Scipy
导入了Scipy,下面是来自网络搜索的关于Scipy的一些知识点
- Scipy:是一个高级的科学计算库,它与Numpy联系很密切
- Scipy一般都是操控Numpy数组来进行科学计算
- Scipy有很多子模块可以应对不同的应用,例如插值运算、优化算法、图像处理、数学统计等
- scipy.io:数据输入输出
- loadmat :是 SciPy 库中的一个函数,可以用于从 MATLAB .mat 文件中读取数据,将其转换成 Python 对象并返回。一般如下展示
# 通过 loadmat 函数读取了名为 data.mat 的文件中的数据。
# 函数返回的是一个 Python 字典,其中包含了文件中所有变量名及其对应的值。
import scipy.io as sio
sio.loadmat('data.mat')

矩阵相乘
- 矩阵乘积
C=A⋅B,矩阵乘积是两个矩阵之间的运算,它将两个矩阵中的对应元素相乘,并将这些乘积相加得到一个新的矩阵。
对于二维矩阵,矩阵乘积,对于一维矩阵,内积
np.dot(A,B)
np.matmul(a,b)
a @ b
- 数量积
也称点积或内积,是两个向量的对应分量逐一相乘,再将相乘结果相加得到的标量值
np.multiply(A,B) 或 *
数量积是两个向量对应分量的乘积相加,结果是一个标量。而矩阵乘积是利用两个矩阵中的元素进行相乘和相加的操作,结果是另一个矩阵。

1.导包
# 导包
import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio
2.读取数据
data = sio.loadmat('ex3data1.mat')
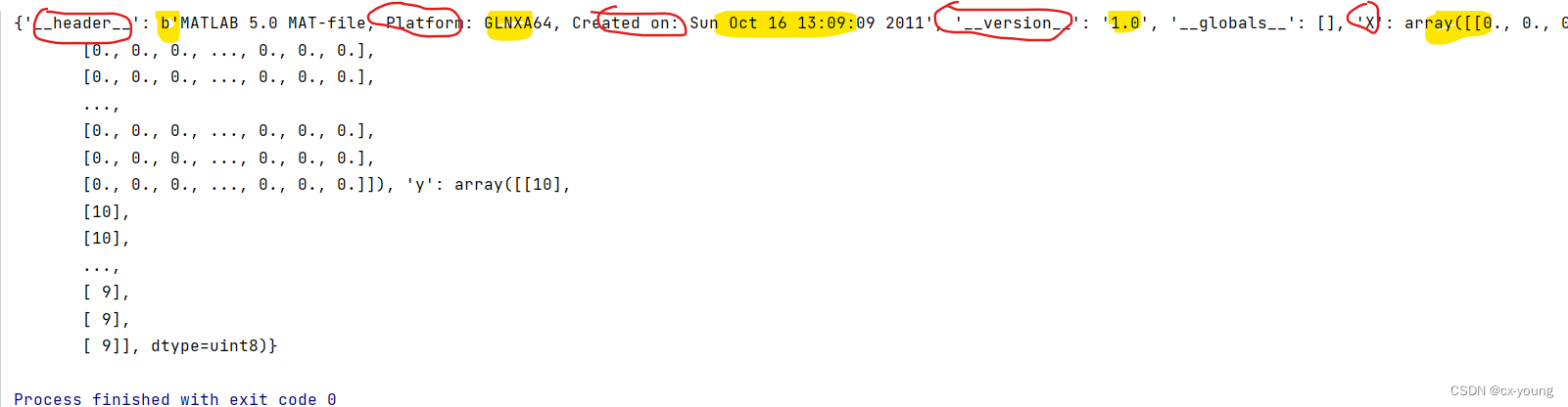
print(data) # 查看数据data,格式
如下图展示,data是字典格式,逗号是把字典项之间进行隔开,冒号前即红色的key,冒号后即黄色的是value
# 查看data的类型 字典类型
print(type(data)) # <class 'dict'>
# 获取data下所有的key的值
print(data.keys()) # dict_keys(['__header__', '__version__', '__globals__', 'X', 'y'])
# 取data中key值为X的数据
raw_X = data['X']
# 取data中key值为y的数据
raw_y = data['y']
# 查看raw_X,raw_y的维度
print(raw_X.shape, raw_y.shape) # (5000, 400) (5000, 1)
# (5000, 400) 意思是5000个训练样例,特征是400维的 由于我们输入的是一张张的图片,
# 其中20×20像素灰度图像的数字,每个像素由一个浮点数表示,该浮
# 点数表示该位置的灰度强度。其实每个训练样例是一个20*20像素的网格被展开成400维的向量。
# 将二维的像素矩阵展平为一维向量。
# (5000, 1)
随机打印一张图片
# 随机的打印一张图片
def plot_an_image(X):
# 从 0 到 4999 中随机选择一个整数
pick_one = np.random.randint(5000)
# 取出这个图片,pick_one表示训练样例所处行,逗号后面的冒号表示取该行的所有列
image = X[pick_one, :]
# 画出该图片
# 使用fig对象来设置整个图形的属性,如图形大小、标题等;
# 而使用ax对象来绘制具体的图形元素,如曲线、散点图等。
# figsize=(1, 1)设置图片尺寸
fig, ax = plt.subplots(figsize=(1, 1))
# imshow Matplotlib的一个函数,把图像数据可视化为20x20像素的灰度图像。
# reshape维度的变化,恢复成(20,20)
# .T转置是为了正着显示
ax.imshow(image.reshape(20, 20).T, cmap='gray_r')
# 不想显示x或y轴的刻度
'''plt.yticks([]) 是Matplotlib库中的一个函数,用于设置y轴刻度。
其中,传入一个空的列表([])作为参数,表示将y轴上的刻度设置为空,
即不显示y轴的任何刻度。以达到更好的可视化效果。'''
plt.xticks([])
plt.yticks([])
plt.show()
plot_an_image(raw_X)
运行结果:

随即打印100张图片
def plot_100_image(X):
# 从0到len(X)-1的整数范围内随机选择100个整数
sample_index = np.random.choice(len(X), 100)
print(sample_index)
images = X[sample_index, :]
print(type(images)) # <class 'numpy.ndarray'>
print(images.ndim) # 2维
print(images.shape) # (100, 400)
# 画出这一百个图片
# sharex=True 指定子图共享x轴 使用相同的x轴刻度和范围
fig, ax = plt.subplots(nrows=10, ncols=10, figsize=(8, 8), sharex=True, sharey=True)
# 显示图像
for r in range(10):
for c in range(10):
# imshow函数将该位置上的图像数据可视化为20x20像素的灰度图像。
# 10 * r + c计算当前子图所对应的图像位置
# images[10 * r + c],这是因为images中的图像被扁平化表示为了一维行向量,而不是按照二维图像进行排列的。
# 因此,我们需要通过索引计算来获取图像数据的位置,而不是直接使用行列索引。
# 对于一维数组,只能使用行索引来获取对应位置上的元素,所以需要使用10 * r + c来获取所需的图像位置。
ax[r, c].imshow(images[10 * r + c].reshape(20, 20).T, cmap='gray_r')
# 不显示xy轴的刻度
plt.xticks([])
plt.yticks([])
plt.show()
plot_100_image(raw_X)
运行结果:

3.损失函数和梯度向量
# 以前是选择损失函数,使用梯度下降函数去最小化损失函数,本次非也
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# theta在此要放到第一位,因为分类器那里用到的函数theta是作为要优化的参数,其他的参数是args
def costFunction(theta, X, y, lamda):
A = sigmoid(X @ theta)
first = y * np.log(A)
second = (1 - y) * np.log(1 - A)
# reg = np.sum(np.power(theta[1:], 2)) * (lamda / (2 * len(X)))
reg = theta[1:] @ theta[1:] * (lamda / (2 * len(X)))
return -np.sum(first + second) / len(X) + reg
# 梯度下降不需要整个迭代过程了
# 只需要梯度向量
def gradient_reg(theta, X, y, lamda):
reg = theta[1:] * (lamda / len(X))
# 向 reg 数组的第一行插入一个值为 0 的元素。
reg = np.insert(reg, 0, values=0, axis=0)
# wj = wj - a * 梯度向量 它是一个 n×1 的列向量,其中 n 是参数向量 θ 的长度。
first = (X.T @ (sigmoid(X @ theta) - y)) / len(X)
return first + reg
4.数据处理
# 数据处理
# 将输入数据 X 矩阵中的第一列插入一个值为 1 的向量
# 这个向量代表偏置项(bias term),也就是偏移量或截距
# 在每个样本的特征向量前面添加一个 1,表示该特征向量中的偏置项取值为 1
# 添加偏置项1,可以将模型中的截距项权重独立出来,方便模型的求解和表达。
# 同时,添加偏置项也可以使得模型对数据集的拟合能力更强,提高模型的泛化能力。
X = np.insert(raw_X, 0, values=1, axis=1)
# 对y进行降维 算准确率的时候比较方便
y = raw_y.flatten()
print(X.shape) # (5000, 401)
print(y.shape) # (5000,)
5.多分类算法
# 多类分类算法 一对多策略思想
# 输入:
# 1.训练数据集X,形状为(m,n)m表示样本个数,n表示特征向量
# 2.训练数据集对应的标签y 形如(m,),其中yi属于{1,2,...,K}表示第i个样本所属的类别
# 3.正则化系数lamda,用于防止过拟合
# 4.样本类别数K
# 输出:
# 每个类别对应的模型参数theta
def one_vs_all(X, y, lamda, K):
# 获取特征数量n
n = X.shape[1]
# 初始化一个 K x n 的模型参数矩阵,表示K个类别对应的模型参数,其中n是特征数量
theta_all = np.zeros((K, n))
# for循环遍历每一个类别i属于{1,2,...,K}
for i in range(1, K + 1):
# 对于每个类别i,初始化一个n维的参数theta_i
theta_i = np.zeros(n, )
# 对于当前类别i,使用TNC算法训练逻辑回归模型,得到对应的theta_i
# TNC 算法是一种优化算法,用来寻找损失函数的最小值
res = minimize(fun=costFunction, # 损失函数,用于计算损失值
x0=theta_i, # 初始参数theta_i
args=(X, y == i, lamda), # args:其他参数,包括训练集X,样本标签y == i和正则化系数lamda
method='TNC', # 优化算法,此处使用的TNC算法
jac=gradient_reg) # jac:梯度函数,用于计算梯度值
# 将得到的theta_i存放到模型参数矩阵的第i-1行(因为数组下标从0开始)
theta_all[i - 1, :] = res.x
# 返回模型参数矩阵
return theta_all
lamda = 1
K = 10
theta_final = one_vs_all(X, y, lamda, K)
print(theta_final)
theta_final:

6.预测
# 预测
# X 测试样本集,形状为 (m,n),其中 m 表示样本个数,n 表示特征数量
# theta_final 模型参数矩阵,形状是(K,n),K是样本类别数,即在训练过程中所得到的参数矩阵
def predict(X, theta_final):
# X:(5000,401) theta_final(10,401)所以要转置 最后m x K的矩阵h是(5000,10)的矩阵
h = sigmoid(X @ theta_final.T)
# print(h.shape) # (5000, 10)
# axis=1意味着按行求最大值的下标,
# 即将每个样本的预测概率(即h中的每一行)和它们对应的类别(即h中的每一列)进行比较
# 找到概率最大的那个类别所在的列下标
# 假设有3个测试样本,他属于4个类别的概率为:
# h = [[0.2, 0.1, 0.5, 0.2],
# [0.6, 0.1, 0.2, 0.1],
# [0.3, 0.3, 0.2, 0.2]]那么np.argmax(h, axis=1)将返回一个长度为3的一维数组,即(3,)其中的元素分别2,0,0
# np.argmax(h, axis=1)返回结果是一个一维数组,记录了每个行向量中最大值所在的索引,因此输出的数组形状应该是一个长度为 m 的一维数组
h_argmax = np.argmax(h, axis=1)
print(h_argmax.shape) # 本题是(5000,)
# np.argmax() 返回的索引是从 0 开始的,而在逻辑回归模型的实现中,类别编号是从 1 开始的,
# 因此我们需要将它们加上 1,使得 h_argmax 表示每个测试样本所属的实际类别
return h_argmax + 1
y_pred = predict(X, theta_final)
acc = np.mean(y == y_pred)
print(acc) # 0.9446
神经网络实现前向传播
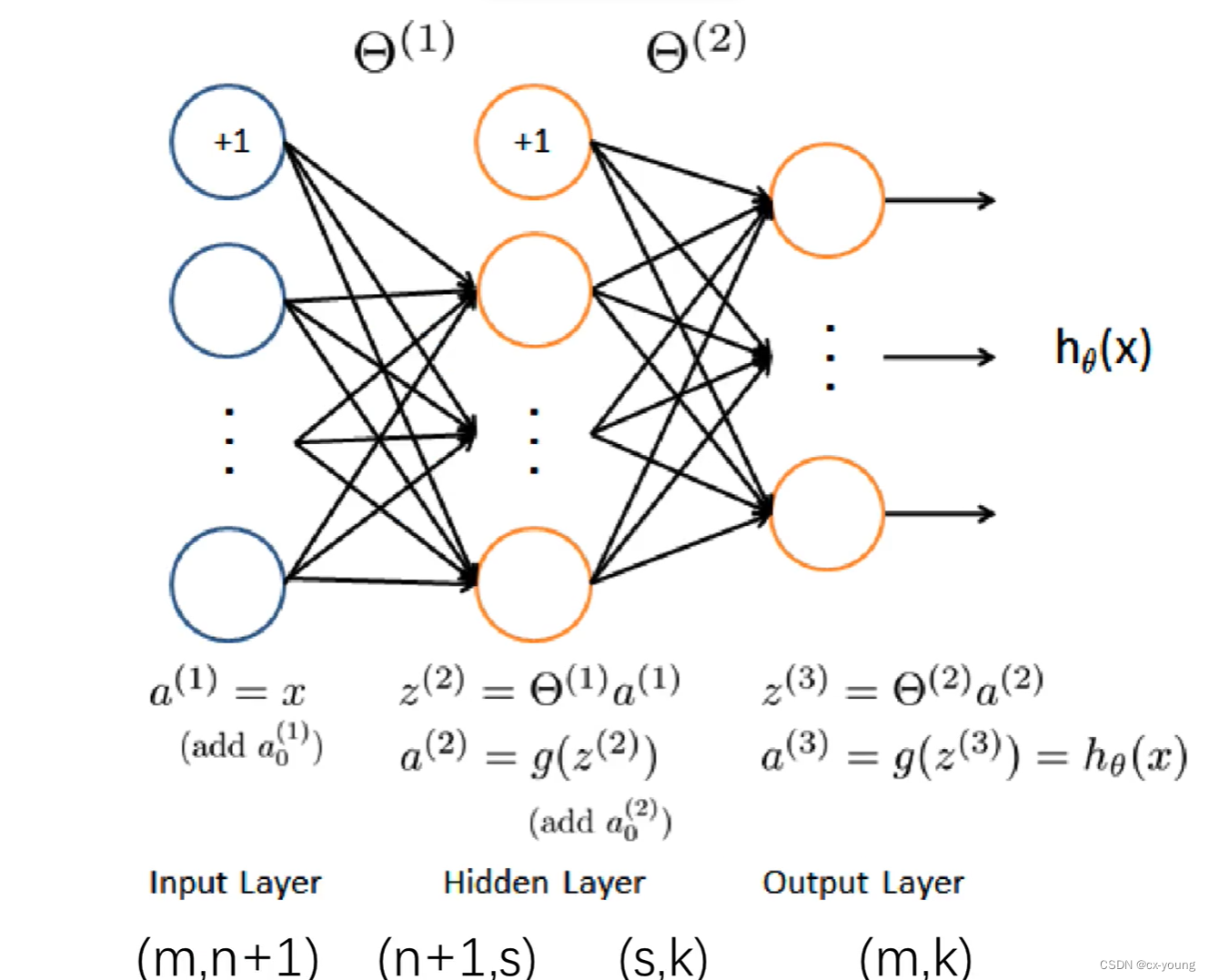
神经网络多分类问题。
本案例的主要目的是为了了解神经网络的传递过程,即了解神经网络如何从输入层传递到最后一层,并进行输出的,参数权重是已经训练好的,拿来用就行,并没有很复杂的推导过程,如果想知道怎样推导的,继续学下去。
图片来自网络
a(1)是输入层,(m,n+1):+1是因为偏置项,也就是本来n个特征,加了一个特征
权重参数θ1(n+1,s),s是隐藏层的单元个数,也要加偏置项
g是激活函数,θ2(s,k) k最终输出类别
a(3) 最终预测值
1.导包
# 数据集:ex3data1.mat
# 参数:ex3weights.mat
import numpy as np
import scipy.io as sio
2.读取数据
data = sio.loadmat('ex3data1.mat')
raw_X = data['X']
raw_y = data['y']
# 插入偏置项
# 即在特征矩阵raw_X的第一列(即axis=1)插入一个元素值为1的列向量,这个元素通常被称为偏置项,用来对应线性回归模型中的截距
X = np.insert(raw_X, 0, values=1, axis=1)
print(X.shape) # (5000, 401)
y = raw_y.flatten()
print(y.shape) # (5000,)
# 获取权重参数theta
theta = sio.loadmat('ex3weights.mat')
print(theta.keys()) # dict_keys(['__header__', '__version__', '__globals__', 'Theta1', 'Theta2'])
theta1 = theta['Theta1'] # 输入层到隐藏层的权重参数
theta2 = theta['Theta2'] # 隐藏层到输出层的权重参数
# 查看维度
print(theta1.shape, theta2.shape) # theta1:(25, 401) (n+1,s)s是隐藏层的单元个数,也要加偏置项 theta2:(10, 26)(s, k)
3.实现前向传播
# 激活函数
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# 输入层 对输入数据X进行预处理,将其插入偏置项1后的X赋值给a1
a1 = X
print(X.shape) # (5000, 401)(m,n+1)
# 通过第一层(隐藏层)的权重矩阵theta1 将输入数据映射到隐藏层进行计算
# 得到隐藏层的输入值z2和经过激活函数处理的激活值a2
z2 = X @ theta1.T
# 激活函数使用的sigmoid函数,它将z2映射到[0,1]区间内
a2 = sigmoid(z2) # 激活函数
print(a2.shape) # (5000, 25)
# 将偏置项1插入到a2中,得到新的矩阵a2
a2 = np.insert(a2, 0, values=1, axis=1)
print(a2.shape) # (5000, 26)
# 根据第二层(输出层)的权重矩阵theta2,将经过第一层隐藏层的输出值a2映射到输出层进行计算
z3 = a2 @ theta2.T
# 得到输出层的输入z3和经过激活函数处理的激活值a3
a3 = sigmoid(z3) # 最终预测值
print(a3.shape) # (5000, 10)
4.查看准确率
# 根据模型的输出a3,通过np.argmax(a3, axis=1)函数,找到每个样本在10个类别中概率最大的预测标签
y_pred = np.argmax(a3, axis=1)
y_pred = y_pred + 1
# 计算准确率
# 将预测标签的平均值与实际标签进行比较,如果相同则认为预测准确
acc = np.mean(y_pred == y)
print(acc) # 0.9752
感谢https://www.bilibili.com/video/BV1mt411p7kG?p=1&vd_source=b3d1b016bccb61f5e11858b0407cc54e