目录
- 3D Transformations(三维变换)
- Viewing transformation(观测变换)
- View/Camera Transformation(视图变换)
- What is view transformation(什么是视图变换)?
- How to perform view transformation?(如何进行视图变换呢?)
- Projection Transformation(投影变换)
- Orthographic Projection(正交投影)
- 变换矩阵
- Perspective Projection(透视投影)
- 参考资源
3D Transformations(三维变换)
延续上节课的内容:
使用齐次坐标进行表示三维的点或者向量:
- 3D point = ( x , y , z ) T (x,y , z)^T (x,y,z)T
- 3D vector = ( x , y , z ) T (x, y, z)^T (x,y,z)T
新的内容:
在三维空间中,分别绕
x
x
x,
y
y
y,
z
z
z轴旋转操作:
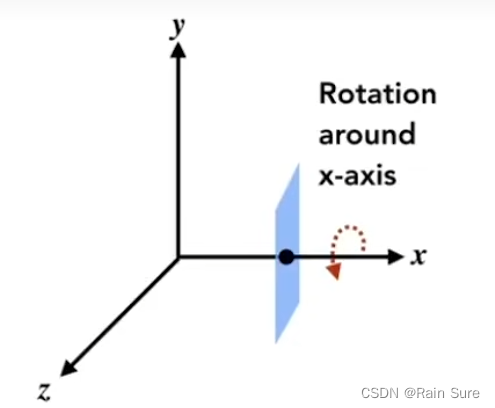
R
x
(
α
)
=
(
1
0
0
0
0
cos
α
−
sin
α
0
0
sin
α
cos
α
0
0
0
0
1
)
\mathbf{R}_{x}(\alpha)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)
Rx(α)=
10000cosαsinα00−sinαcosα00001
R y ( α ) = ( cos α 0 sin α 0 0 1 0 0 − sin α 0 cos α 0 0 0 0 1 ) \mathbf{R}_{y}(\alpha)=\left(\begin{array}{cccc} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 &0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) Ry(α)= cosα0−sinα00100sinα0cosα00001
R z ( α ) = ( cos α − sin α 0 0 sin α cos α 0 0 0 sin α 1 0 0 0 0 1 ) \mathbf{R}_{z}(\alpha)=\left(\begin{array}{cccc} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & \sin \alpha & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) Rz(α)= cosαsinα00−sinαcosαsinα000100001
任意的三维的旋转都可以写成分别绕
x
x
x轴,绕
y
y
y轴,绕
z
z
z轴的组合:
R
x
y
z
(
α
,
β
,
γ
)
=
R
x
(
α
)
R
y
(
β
)
R
z
(
γ
)
\mathbf{R}_{xyz}(\alpha, \beta, \gamma) = \mathbf{R}_{x}(\alpha)\mathbf{R}_{y}(\beta)\mathbf{R}_{z}(\gamma)
Rxyz(α,β,γ)=Rx(α)Ry(β)Rz(γ)
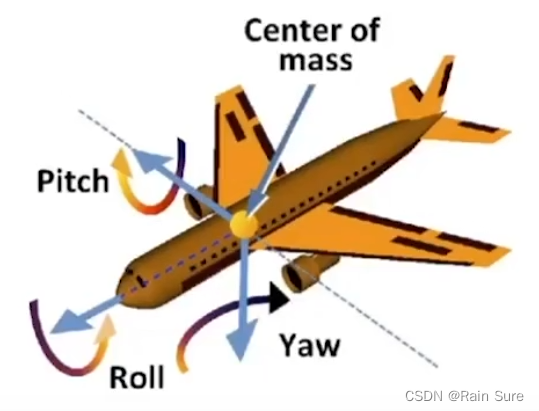
这三个角又被称为欧拉角(Euler angles)。
常用于飞行模拟器:滚转,俯仰,偏航。
罗德里格旋转公式(Rodrigues’ Rotation Formula):
绕旋转轴 n ⃗ \vec{n} n旋转角度 α \alpha α,默认轴的起点在原点上。
R ( n , α ) = cos ( α ) I + ( 1 − cos ( α ) ) n n T + sin ( α ) ( 0 − n z n y n z 0 − n x − n y n x 0 ) ⏟ N \mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc} 0 & -n_{z} & n_{y} \\ n_{z} & 0 & -n_{x} \\ -n_{y} & n_{x} & 0 \end{array}\right)}_{\mathbf{N}} R(n,α)=cos(α)I+(1−cos(α))nnT+sin(α)N 0nz−ny−nz0nxny−nx0
Viewing transformation(观测变换)
View/Camera Transformation(视图变换)
What is view transformation(什么是视图变换)?
思考一下,如何拍一张照片?
- 找到一个合适的位置然后摆一个Pos(model transformation),这一步是模型变换
- 找一个好的角度来摆放相加(view transformation),这一步就是视图变换。
- 拍照,这一步是投影变换。
模型、视图、投影变换,简称MVP变换。
How to perform view transformation?(如何进行视图变换呢?)
首先,要确定相机,主要有三个参数:
- 位置: e ⃗ \vec{e} e
- 视线方向: g ^ \hat{g} g^
- 向上的方向: t ^ \hat{t} t^
当相机和物体同步移动时,拍出来的照片完全相同。
所以,我们通常将相机位置进行固定:
- 相机位于原点,向上的方向是 y y y轴,视线方向是 − z -z −z方向。
- 并且将其它物体随着相机移动。
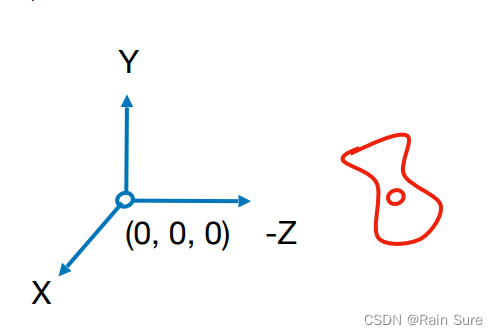
需要进行的改变:
- 将 e ⃗ \vec{e} e移动到原点。
- 将 g ⃗ \vec{g} g旋转到 − Z ⃗ -\vec{Z} −Z。
- 将 t ⃗ \vec{t} t旋转到 Y Y Y。
- 将 ( g ⃗ × t ⃗ ) (\vec{g}\times \vec{t} ) (g×t)旋转到 X X X。
先考虑平移,再考虑旋转:
-
首先,移动到原点:
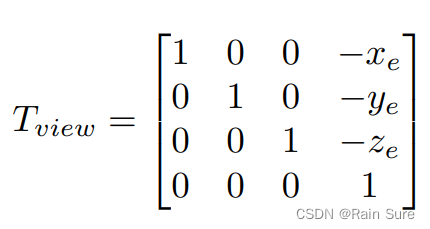 c
c -
旋转:
直接旋转的变换矩阵不好写,但是反过来考虑很好写,所以我们可以先将逆矩阵写出来,再求一次逆就可以得到变换矩阵了。
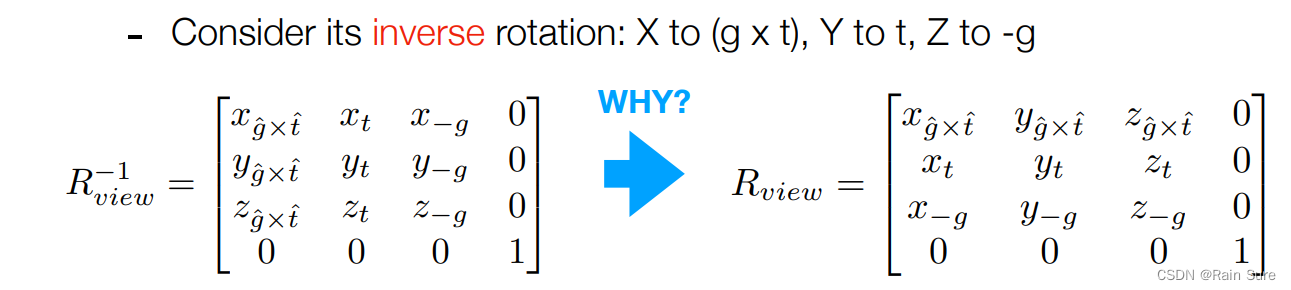
因为旋转矩阵是正交矩阵,所以直接求转置就可以得到逆矩阵了。
最终的变换矩阵就可以得到了:
M
v
i
e
w
=
R
v
i
e
w
T
v
i
e
w
M_{view} = R_{view}T_{view}
Mview=RviewTview
Projection Transformation(投影变换)
计算机图形学中的投影:
- 3D to 2D
- 正交投影
- 透视投影
这两种投影的本质区别就是是否具有近大远小的特征。
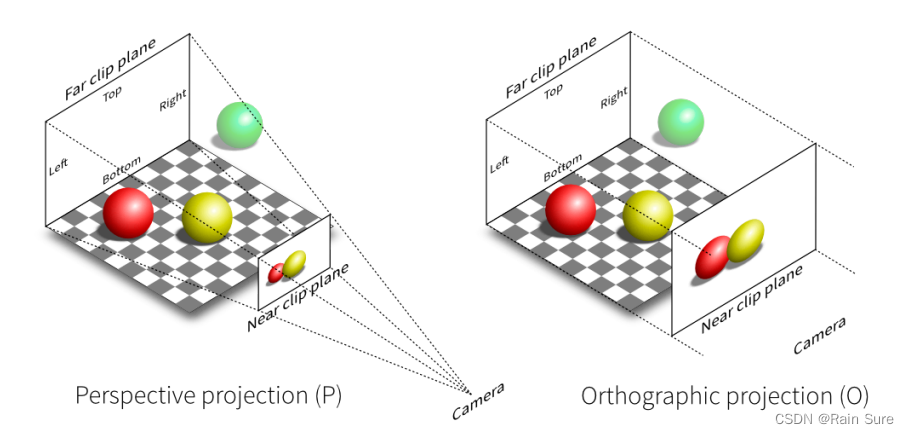
Orthographic Projection(正交投影)
一种简单的理解方式:
- 将相机摆放在原点,朝 − Z -Z −Z方向看,向上方向为 Y Y Y。
- 扔掉 Z Z Z坐标。
- 将结果矩阵平移和缩放到 [ − 1 , 1 ] 2 [-1, 1]^2 [−1,1]2中。
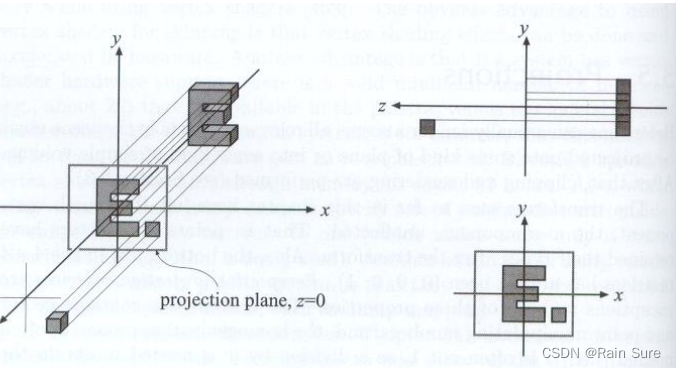
一种正式一点的做法:
我们希望将一个立方体
[
l
,
r
]
×
[
b
,
t
]
×
[
f
,
n
]
[l, r] \times [b, t] \times [f, n]
[l,r]×[b,t]×[f,n]映射到一个标准的立方体上去
[
−
1
,
1
]
3
[-1, 1]^3
[−1,1]3。
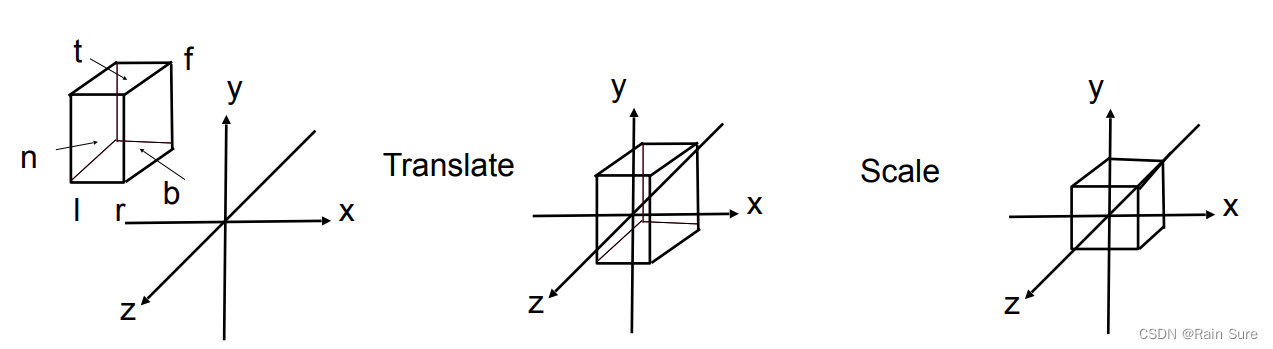
变换矩阵
首先,将中心移动到原点,再进行缩放将宽度变为2。
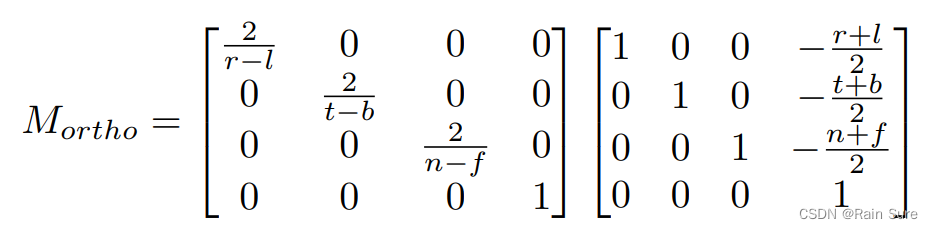
Perspective Projection(透视投影)
在计算机图形学、艺术、视觉系统中最常见的投影。
近大远小。
平行线将不在平行,收敛到一点。
如何进行透视投影呢?
- 先挤成一个长方体;
- 再对长方体做一次正交投影。
第一步的过程可以使用一个变换矩阵来描述:
M
p
e
r
s
p
−
>
o
r
t
h
o
M_{persp -> ortho}
Mpersp−>ortho;
第二步再使用一个正交投影变换矩阵来进行变换:
M
o
r
t
h
o
M_{ortho}
Mortho;
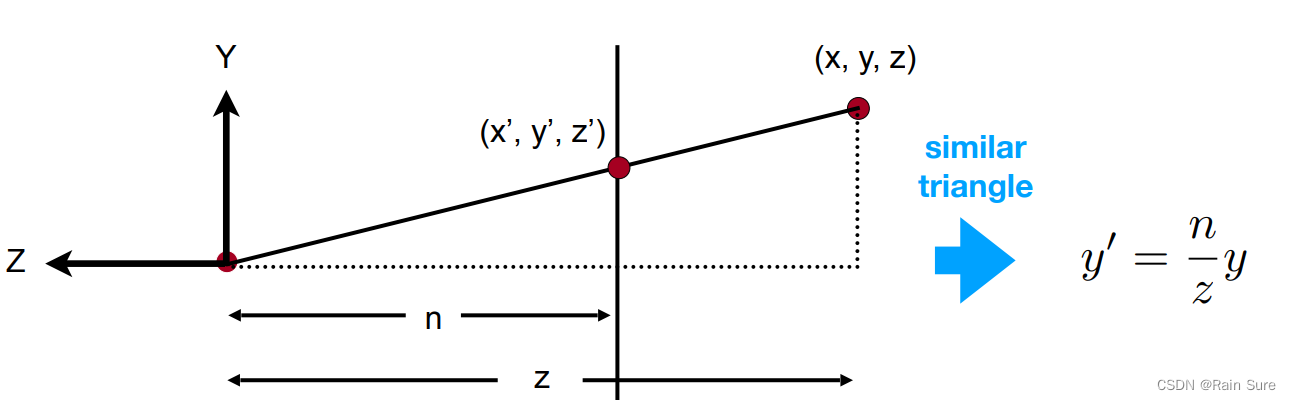
根据相似三角形,容易得到
y
′
=
n
z
y
y \prime = \frac{n}{z} y
y′=zny,
x
′
=
n
z
x
x \prime = \frac{n}{z} x
x′=znx;
在齐次坐标下:
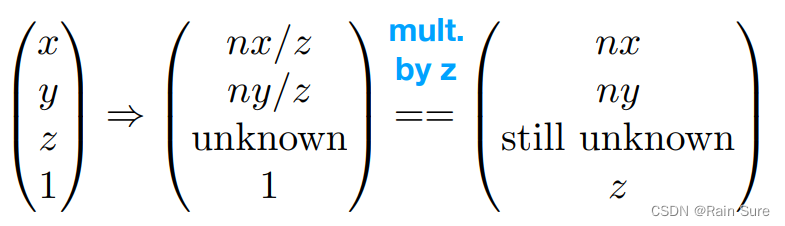
通过,已知的三个信息,我们可以推出变换矩阵的部分信息:
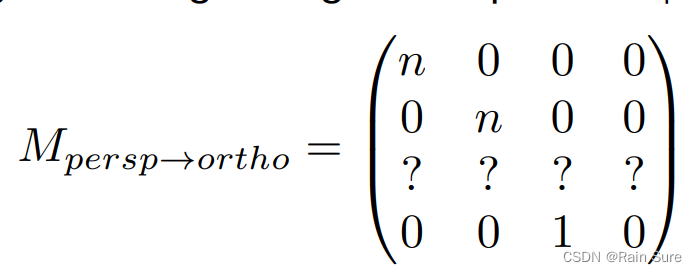
两个重要条件:
- 近平面上的任何点坐标不会发生任何变化。
- 远平面的点的 z z z坐标不会发生任何变化。

因此,变换矩阵的第三行一定是
(
0
,
0
,
A
,
B
)
(0, 0, A, B)
(0,0,A,B)的形式。
(
0
,
0
,
f
)
(0, 0, f)
(0,0,f)这个点经过挤压后,仍然位于
(
0
,
0
,
f
)
(0, 0, f)
(0,0,f)。
因此,可以得到如下方程:
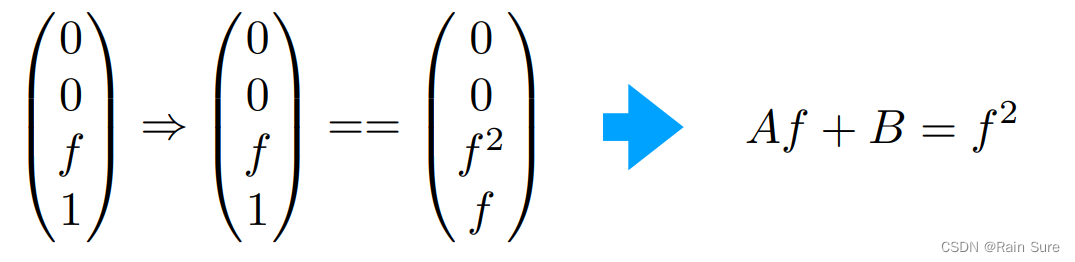
通过两个方程,就可以得到
A
A
A和
B
B
B的值:

综上,变换矩阵
M
p
e
r
s
p
−
>
o
r
t
h
o
M_{persp -> ortho}
Mpersp−>ortho就得到了。
参考资源
GAMES101 Lecture 04