参考：

0x3f：从集合论到位运算，常见位运算技巧分类总结！https://leetcode.cn/circle/discuss/CaOJ45/

状态压缩DP详细讲解 https://zhuanlan.zhihu.com/p/599427567

【动态规划学习】状压/子集 DP https://leetcode.cn/circle/article/CD6iai/

位运算和状态压缩DP

集合与位运算

0x3f：从集合论到位运算，常见位运算技巧分类总结！https://leetcode.cn/circle/discuss/CaOJ45/

集合可以用二进制表示，二进制从低到高第 i 位为 1 表示 i 在集合中，为 0 表示 i 不在集合中。例如集合 {0,2,3} 可以用二进制数 1101 表示；反过来，二进制数 1101 就对应着集合 {0,2,3}。

利用位运算「并行计算」的特点，我们可以高效地做一些和集合有关的运算。按照常见的应用场景，可以分为以下四类：

集合与集合
集合与元素
遍历集合
枚举集合

一、集合与集合

其中 & 表示按位与，∣ 表示按位或，⊕ 表示按位异或，∼ 表示按位取反。

其中「对称差」指仅在其中一个集合的元素。

术语	集合	位运算	举例	举例
交集	A ∩ B	a & b	{0,2,3} ∩ {0,1,2}= {0,2}	1101 & 0111= 0101
并集	A ∪ B	a ∣ b	{0,2,3}∪ {0,1,2}= {0,1,2,3}	1101 ∣ 0111= 1111
对称差	A Δ B	a ⊕ b	{0,2,3} Δ {0,1,2}= {1,3}	1101 ⊕ 0111= 1010
差	A ∖ B	a & ∼b	{0,2,3} ∖ {1,2}= {0,3}	1101 & 1001= 1001
差（子集）	A ∖ B (B⊆A)	a ⊕ b	{0,2,3} ∖ {0,2}= {3}	1101 ⊕ 0101= 1000
包含于	A ⊆ B	a & b = a a ∣ b = b	{0,2} ⊆ {0,2,3}	0101 & 1101=0101 0101 ∣ 1101=1101

二、集合与元素

通常会用到移位运算。

其中 << 表示左移，>> 表示右移。

注：左移 i 位相当于乘 2^i，右移 i 位相当于除 2^i。

术语	集合	位运算	举例	举例
空集	∅	0
单元素集合	{i}	1 << i	{2}	1 << 2
全集	U={0,1,2,⋯n−1}	(1 << n)−1	{0,1,2,3}	(1 << 4)−1
补集	$_uS$ =U∖S	∼s 或者 ((1 << n)−1)⊕s
属于	i ∈ S	(s >> i) & 1=1	2∈{0,2,3}	(1101 >> 2) & 1=1
不属于	i ∉ S	(s >> i) & 1=0	1∉{0,2,3}	(1101 >> 1) & 1=0
添加元素	S ∪ {i}	s ∣ (1 << i)	{0,3}∪{2}	1001 ∣ (1 << 2)
删除元素	S ∖ {i}	s & ∼(1 << i)	{0,2,3}∖{2}	1101&∼(1 << 2)
删除元素（一定在集合中）	S ∖ {i}（i∈S）	s ⊕ (1 << i)	{0,2,3}∖{2}	1101⊕(1 << 2)
删除最小元素		s & (s−1)		见下

      s = 101100
    s-1 = 101011 // 最低位的 1 变成 0，同时 1 右边的 0 都取反，变成 1
s&(s-1) = 101000

此外，某些数字可以借助标准库提供的函数算出：

术语	Java
集合大小（元素个数）	`Integer.bitcount(s)`
二进制长度（减一得到集合中的最大元素）	`32-Integer.numberOfLeadingZeros(s)`
集合中的最小元素	`Integer.numberOfTrailingZeros(s)`

特别地，只包含最小元素的子集，即二进制最低 1 及其后面的 0，也叫 lowbit，可以用 s & -s 算出。举例说明：

     s = 101100
    ~s = 010011
(~s)+1 = 010100 // 根据补码的定义，这就是 -s   最低 1 左侧取反，右侧不变
s & -s = 000100 // lowbit

三、遍历集合

设元素范围从 0 到 n−1，挨个判断元素是否在集合 s 中：

for (int i = 0; i < n; i++) {
    if (((s >> i) & 1) == 1) { // i 在 s 中
        // 处理 i 的逻辑
    }
}

四、枚举集合

设元素范围从 0 到 n−1，从空集 ∅ 枚举到全集 U：

for (int s = 0; s < (1 << n); s++) {
    // 处理 s 的逻辑
}

设集合为 s，从大到小枚举 s 的所有非空子集 sub：

for (int sub = s; sub > 0; sub = (sub - 1) & s) {
    // 处理 sub 的逻辑
}

如果要从大到小枚举 s 的所有子集 sub（从 s 枚举到空集 ∅），可以这样写：

int sub = s;
do {
    // 处理 sub 的逻辑
    sub = (sub - 1) & s;
} while (sub != s);

注：还可以枚举全集 U 的所有大小恰好为 k 的子集，这一技巧叫做 Gosper’s Hack https://www.bilibili.com/video/BV1na41137jv/

// 枚举全集 U 的所有大小恰好为 k 的子集
for(int s = 0; s < (1 << n); s++){
    if(Integer.bitCount(s) == k){
        // 处理 sub 的逻辑
    }
}

状态压缩DP与最短哈密顿(Hamilton)路径问题

状态压缩DP：

https://zhuanlan.zhihu.com/p/599427567

在讲状压dp之前，我们应该清楚dp是解决多阶段决策最优化问题的一种思想方法，即利用各个阶段之间的关系，逐个求解，最终求得全局最优解。

我们通常需要确认原问题与子问题、动态规划状态、边界状态、状态转移方程。

动态规划多阶段一个重要的特性就是无后效性，即“未来与过去无关”。无后效性就是对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的发展。换句话说，当前的状态是此前历史的一个完整总结，此前的历史只能通过当前的状态去影响过程未来的演变。

对于动态规划，如何定义状态是至关重要的，因为状态决定了阶段的划分，阶段的划分保证了无后效性。

状态压缩DP其实是一种暴力的算法，因为它需要遍历每个状态，而每个状态是多个事件的集合，也就是以集合为状态，一个集合就是一个状态。集合问题一般是指数复杂度的NP问题，所以状态压缩DP的复杂度仍然是指数的，只能用于小规模问题的求解。

为了方便地同时表示一个状态的多个事件，状态一般用二进制数来表示。一个数就能表示一个状态，通常一个状态数据就是一个一串0和1组成的二进制数，每一位二进制数只有两种状态，比如说硬币的正反两面，10枚硬币的结果就可以用10位二进制数完全表示出来，每一个10位二进制数就表示了其中一种结果。

使用二进制数表示状态不仅缩小了数据存储空间，还能利用二进制数的位运算很方便地进行状态转移。

【动态规划学习】状压/子集 DP https://leetcode.cn/circle/article/CD6iai/

1、状态压缩 是 DP 的一个小技巧，一般应用在集合问题中（状压 DP 又叫 子集 DP(DP on Subsets)）。当 DP 状态 是集合时，把集合的组合或排列用一个 二进制整数 表示，这个二进制整数的 0/1 组合表示集合的一个子集，从而把对 DP 状态 的处理转换为二进制的位操作，让代码变得简洁易写（注：相对集合操作而言），同时提高算法效率。从二进制操作简化集合处理的角度看，状态压缩 也是一种 DP 优化方法。

注：DP 优化的方法有很多，其中 状态压缩 是对 DP 状态表示 的优化~

2. 状压DP 经典问题 —— 最短哈密顿(Hamilton)路径问题

状态压缩 DP 常常用 Hamilton（旅行商）问题作为引子。

最短 Hamilton 路径 - AcWing

问题描述：给定一个有权无向图，包括 $n$ 个点，标记 $0 \sim n - 1$ ，以及连接 $n$ 个点的边，求从起点 $0$ 到终点 $n - 1$ 的最短路径。要求必须经过所有点，而且只经过一次。 $1 \leq n \leq 20$ 。

先尝试暴力解法，枚举 n 个点的全排列。共有 n! 个全排列，一个全排列就是一条路径，计算每个全排列的路径长度，需要做 n 次加法。在所有路径中找最短路径，总的时间复杂度为 $O (n \times n!)$ 。

时间复杂度分析：10! ≈ 3x10^6，当 n = 14时，14! > 10! × 10^4

使用DP求解Hamilton问题

如果用状态压缩 DP 求解，能把时间复杂度降低到 $O(n^2\times2^n)$ 。

状态定义： 设 S 为图的一个子集，用 dp[S][j]表示集合 S 内最短的Hamilton问题，即从起点 0 出发，经过 S 中的所有点，到达终点 j 的最短路径 (集合 S 中包含点) 。然后根据 DP 的思路，让 S 从最小的子集逐步扩展到整个图，最后得到的 dp[N][n-1] 就是答案，N 表示包含图上所有点的集合。

状态转移： 如何求 dp[S][j]? 可以从小问题 S - j 递推到大问题 S。

其中，S - j表示从集合 S 中去掉，即不包含 j 点的集合

如何从 S - j递推到 S? 设为 S - j 中的一个点，把 0~ j 的路径分为两部分: 0->1... ->k 和 (k +1) ->...-> j。以 k 为变量，枚举 s-j 中的所有点，找出最短路，状态转移方程为:
$dp[S][j] = min({dp[S - j][k] + dist(k, j)}),k∈(S-j)$

集合 S 初始时只包含起点 0，然后逐步将图中的点包含进来，直到最后包含所有点。

#include<bits/stdc++.h>
using namespace std;
int n, dp[1 << 20][21];
int dist[21][21];
int main(){
    // 初始化为最大值
    memset(dp, 0x3f, sizeof(dp));
    cin >> n;
    // 输入图
    for (int i = 0; i < n; i ++)    
        for (int j = 0; j < n; j ++)
            // 输入点之间的距离
            cin >> dist[i][j];
    
    // 开始：集合中只有点 0，起点和终点都是 0
    dp[1][0] = 0;
    // 从小集合扩展到大集合，集合用 S 的二进制表示（遍历集合）         
    for (int S = 1; S < (1 << n); S ++) 
        // 枚举点 j
        for (int j = 0; j < n; j ++)
            // (1) 这个判断与下面的 (2) 同时起作用
            if ((S >> j) & 1)
                // 枚举到达 j 的点 k，k 属于集合 S - j
                for (int k = 0; k < n; k ++)
                    // (2) k 属于集合 S - j，S - j 用 (1) 保证
                    if ((S ^ (1 << j)) >> k & 1)
                    // 把 (1) 和 (2) 写在一起更容易理解，但是效率低一些
                    // if (((S >> j) & 1) && ((S ^ (1 << j)) >> k & 1))
                        dp[S][j] = min(dp[S][j], dp[S ^ (1 << j)][k] + dist[k][j]);
    // 输出：路径包含了所有的点，终点是 n - 1
    cout << dp[(1 << n) - 1][n - 1];
    return 0;
}

位运算与状压DP题单

1、集合论与位运算：

78. 子集
77. 组合
46. 全排列

2、奇偶性判断：

按位异或：①当x是偶数时，x+1 = x ^ 1；②当x是奇数时，x-1 = x^1

按位与：①当x时偶数时，x & 1 = 0；②当x是奇数时，x & 1 = 1

540. 有序数组中的单一元素

3、常见位运算题目

**异或运算本质：消除所有出现次数为偶数的元素。**出现次数为偶数次的数最终都会被异或掉变成0。最后只保留出现次数为奇数次的数。

136. 只出现一次的数字
2401. 最长优雅子数组

按位或：

2411. 按位或最大的最小子数组长度

然后是一些状态压缩 DP。这类题目通常和排列/子集有关，可以先从暴力回溯开始思考，再过渡到记忆化搜索和递推。

1494. 并行课程 II
2741. 特别的排列
1879. 两个数组最小的异或值之和
1125. 最小的必要团队，题解

2172. 数组的最大与和？
1986. 完成任务的最少工作时间段
LCP 53. 守护太空城，题解
2305. 公平分发饼干，题解

更多题目，可以在题库中同时选上「动态规划」和「位运算」这两个标签：链接。

子集状压DP练习题

1494. 并行课程 II

难度困难188

给你一个整数 n 表示某所大学里课程的数目，编号为 1 到 n ，数组 relations 中， relations[i] = [xi, yi] 表示一个先修课的关系，也就是课程 xi 必须在课程 yi 之前上。同时你还有一个整数 k 。

在一个学期中，你最多可以同时上 k 门课，前提是这些课的先修课在之前的学期里已经上过了。

请你返回上完所有课最少需要多少个学期。题目保证一定存在一种上完所有课的方式。

示例 1：

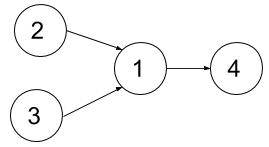
输入：n = 4, relations = [[2,1],[3,1],[1,4]], k = 2
输出：3 
解释：上图展示了题目输入的图。在第一个学期中，我们可以上课程 2 和课程 3 。然后第二个学期上课程 1 ，第三个学期上课程 4 。

示例 2：

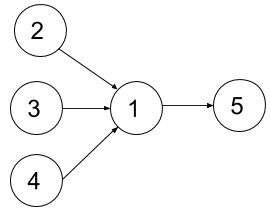
输入：n = 5, relations = [[2,1],[3,1],[4,1],[1,5]], k = 2
输出：4 
解释：上图展示了题目输入的图。一个最优方案是：第一学期上课程 2 和 3，第二学期上课程 4 ，第三学期上课程 1 ，第四学期上课程 5 。

示例 3：

输入：n = 11, relations = [], k = 2
输出：6

提示：

1 <= n <= 15
1 <= k <= n
0 <= relations.length <= n * (n-1) / 2
relations[i].length == 2
1 <= xi, yi <= n
xi != yi
所有先修关系都是不同的，也就是说 relations[i] != relations[j] 。
题目输入的图是个有向无环图。

题解：https://leetcode.cn/problems/parallel-courses-ii/solution/zi-ji-zhuang-ya-dpcong-ji-yi-hua-sou-suo-oxwd/

一、记忆化搜索：

代码实现时，由于先学课程 1，再学课程 2，或者先学课程 2，再学课程 1，都会递归到「学完课程 1 和 2」的状态上。一叶知秋，整个递归中有大量重复递归调用（递归入参相同）。由于递归函数没有副作用，同样的入参无论计算多少次，算出来的结果都是一样的，因此可以用记忆化搜索来优化。

从 i1 出发，求为 1 的位的子集，开始这些为 1 的位全是 1，之后每次减去 1，再与 i1做与运算，得到的 1 所在的位仍然在最初的 i1 所在的位的集合中，只是某些位变为了 0，由于每次只减去 1，所以肯定可以遍历 11111…111 ~ 00000…000 的所有状态，即得到为 1 的位的子集。

class Solution {
    // 定义dfs(i)表示上完集合 i 中的课程，最少需要多少个学期
    // 考虑枚举 i 的大小不超过 k 的非空子集 j，作为一个学期内需要学完的课程
    //          这里 j 中所有元素的先修课必须在 i 的补集中
    // 用一个学期上完 j 中的课程，则剩余课程为i/j ，继续递归计算 dfs(i/j)，所有情况取最小值
    // 递归边界 dfs(空集) = 0
    // 递归入口 dfs(全集)
    int[] pre1, memo;
    int k, u;
    public int minNumberOfSemesters(int n, int[][] relations, int k) {
        this.k = k;
        pre1 = new int[n];
        for(int[] r : relations){
            // r[1] 的先修课程集合，下标改从 0 开始
            pre1[r[1] - 1] |= 1 << (r[0] - 1);
        }
        u = (1 << n) - 1; // 全集
        memo = new int[1 << n];
        Arrays.fill(memo, -1); // -1表示还没计算过
        return dfs(u);
    }

    public int dfs(int i){
        if(i == 0) return 0; // 空集
        if(memo[i] != -1) return memo[i]; // 之前计算过了
        int i1 = 0, ci = u ^ i; // i1 是当前可以学习的课程集合，ci 是 i 的补集(已经学过的课程)
        for(int j = 0; j < pre1.length; j++){
            // pre1[j] 在 i 的补集中，可以学（否则这学期一定不能学）
            if(((i >> j) & 1) == 1 && (pre1[j] | ci) == ci)
                i1 |= 1 << j;
        }
        if(Integer.bitCount(i1) <= k){ // 如果个数小于k，则可以全部学习，不用再枚举子集
            return memo[i] = dfs(i ^ i1) + 1; // dfs(i) = dfs(i \ i1) + 1
        }
        // 可以学的课程超过k个，需要枚举大小为 k 的子集
        int res = Integer.MAX_VALUE;
    
        for(int j = i1; j > 0; j = (j-1) & i1){ // 枚举 i1 的子集 j
            if(Integer.bitCount(j) == k)
                res = Math.min(res, dfs(i ^ j) + 1);
        }
        return memo[i] = res;
    }
}

记忆化搜索转递推

class Solution {
    public int minNumberOfSemesters(int n, int[][] relations, int k) {
        int[] pre1 = new int[n];
        for(int[] r : relations)
            // r[1] 的先修课程集合，下标改从 0 开始
            pre1[r[1] - 1] |= 1 << (r[0] - 1);
        int u = (1 << n) - 1; // 全集
        // 定义f(i)表示上完集合 i 中的课程，最少需要多少个学期
        int[] f = new int[1 << n];
        f[0] = 0;
        for(int i = 1; i < (1 << n); i++){
            int i1 = 0, ci = u ^ i; // i1 是当前可以学习的课程集合，ci 是 i 的补集(已经学过的课程)
            for(int j = 0; j < n; j++)
                // pre1[j] 在 i 的补集中，可以学（否则这学期一定不能学）
                if(((i >> j) & 1) == 1 && (pre1[j] | ci) == ci)
                    i1 |= 1 << j;
            if(Integer.bitCount(i1) <= k){ // 如果个数小于k，则可以全部学习，不用再枚举子集
                f[i] = f[i ^ i1] + 1;
                continue;
            }
            f[i] = Integer.MAX_VALUE;
            for(int j = i1; j > 0; j = (j-1) & i1){ // 枚举 i1 的子集 j
                if(Integer.bitCount(j) == k)
                    f[i] = Math.min(f[i], f[i ^ j] + 1);
            }
        }
        return f[u];
    }
}

2741. 特别的排列

难度中等12

给你一个下标从 0 开始的整数数组 nums ，它包含 n 个 互不相同 的正整数。如果 nums 的一个排列满足以下条件，我们称它是一个特别的排列：

对于 0 <= i < n - 1 的下标 i ，要么 nums[i] % nums[i+1] == 0 ，要么 nums[i+1] % nums[i] == 0 。

请你返回特别排列的总数目，由于答案可能很大，请将它对 109 + 7 取余后返回。

示例 1：

输入：nums = [2,3,6]
输出：2
解释：[3,6,2] 和 [2,6,3] 是 nums 两个特别的排列。

示例 2：

输入：nums = [1,4,3]
输出：2
解释：[3,1,4] 和 [4,1,3] 是 nums 两个特别的排列。

提示：

2 <= nums.length <= 14
1 <= nums[i] <= 109

题解：https://leetcode.cn/problems/special-permutations/solution/zhuang-ya-dp-by-endlesscheng-4jkr/

关键点：

1、为什么可以这个东西可以用记忆化搜索进行优化？

【先选 2 再选 1 然后递归到 4】和【先选 1 再选 2 然后递归到4】都会递归到dfs(*,4)，参数相同，是一个重复的子问题，可以用记忆化搜索解决 O(n!) -> O(2^n)

2、状态压缩DP = ①排列型的回溯、②记忆化搜索=>递推、③集合=>位运算

记忆化搜索

class Solution {
    // 定义dfs(i, j) 表示当前可以选的下标集合为 i, 上一个选的数的下标是j,
    // 转移：从i中选一个下标k
    // 如果 nums[i] % nums[j] == 0 or nums[j] % nums[i] == 0 
    // 则 dfs(i, j) += sum(dfs(i\{k}, k) for k in i)
    // 递归边界：dfs(空集【0】, j) = 1 // 递归到i是空集，说明找到了一个特别的排列
    // 递归入口：dfs(U\{j}, j)
    // 答案： sum(dfs(U\{j}, j) for j in range(n))
    // 时间复杂度 = O(状态个数) * O(单个状态的计算时间) <- 【动态规划的时间复杂度】
    // 			= O(n * 2^n) * O(n)
    private static final int MOD = (int) 1e9 + 7;
    int n;
    int[][] cache;
    int[] nums;
    public int specialPerm(int[] nums) {
        n = nums.length;
        this.nums = nums;
        // cache[i][j] : i是集合的所有情况 2^i个，j表示上一次选的数 n个
        cache = new int[1 << n][n];
        for(int i = 0; i < (1 << n); i++)
            Arrays.fill(cache[i], -1);
        int ans = 0;
        int u = (1 << n) - 1; // 全集
        for(int i = 0; i < n; i++){ // 初始状态下每个数都可以选
            ans = (ans + dfs(u ^ (1 << i), i)) % MOD;
        }
        return ans % MOD;
    }

    public int dfs(int i, int j){
        if(i == 0) return 1;
        if(cache[i][j] >= 0) return cache[i][j];
        int res = 0;
        // 遍历集合
        for(int k = 0; k < n; k++){
            // 判断元素k是否在集合i中(是否可以选)
            if(((i >> k) & 1) == 1){
                if(nums[j] % nums[k] == 0 || nums[k] % nums[j] == 0){ // 题目要求
                    res = (res + dfs(i ^ (1 << k), k)) % MOD;
                }
            }
        }
        return cache[i][j] = res % MOD;
    }
}

转成递推

class Solution {
    private static final int MOD = (int) 1e9 + 7;
    public int specialPerm(int[] nums) {
        int n = nums.length;
        // 定义f[i][j] 表示当前可以选的下标集合为 i, 上一个选的数的下标是j,
        int[][] f = new int[1 << n][n];
        for(int i = 0; i < n; i++)
            f[0][i] = 1;
        // 递归dfs(i,j) ,递推就得循环计算i和j
        // i 从小到大遍历（遍历所有状态集合）
        for(int i = 0; i < (1 << n); i++){
            // 遍历每个元素
            for(int j = 0; j < n; j++){ 
                for(int k = 0; k < n; k++){
                    if(((i >> k) & 1) == 1 && (nums[j] % nums[k] == 0 || nums[k] % nums[j] == 0))
                        f[i][j] = (f[i][j] + f[i ^ (1 << k)][k]) % MOD;
                }
            }
        }
        int ans = 0;
        for(int i = 0; i < n; i++){
            ans = (ans + f[((1<<n)-1)^(1<<i)][i]) % MOD;
        }
        return ans;
    }
}

996. 正方形数组的数目（相似）

难度困难109

给定一个非负整数数组 A，如果该数组每对相邻元素之和是一个完全平方数，则称这一数组为正方形数组。

返回 A 的正方形排列的数目。两个排列 A1 和 A2 不同的充要条件是存在某个索引 i，使得 A1[i] != A2[i]。

示例 1：

输入：[1,17,8]
输出：2
解释：
[1,8,17] 和 [17,8,1] 都是有效的排列。

示例 2：

输入：[2,2,2]
输出：1

提示：

1 <= A.length <= 12
0 <= A[i] <= 1e9

class Solution {
    int[] nums;
    int n;
    int[][] cache;
    public int numSquarefulPerms(int[] nums) {
        this.nums = nums;
        n = nums.length;
        int u = (1 << n) - 1;
        cache = new int[1 << n][n];
        for(int i = 0; i < (1 << n); i++)
            Arrays.fill(cache[i], -1);
        int res = 0;
        for(int i = 0; i < n; i++){
            res += dfs(u ^ (1 << i), i);
        }
        // 去重 : dp 算出来的结果有很多重复的，需要去重，这里用的是乘法原理去重，
	    // 例如1，1，2，2，2，3中全排列去重，两个1交换位置会多算一次（共2次），
        //      三个2交换位置会多算5次（共6次），最后结果除以每个重复数次数的阶乘。
        Map<Integer, Integer> map = new HashMap<>();
        for(int num : nums) map.put(num, map.getOrDefault(num, 0) + 1);
        for(Map.Entry<Integer, Integer> entry : map.entrySet()){
            res /= getFactorial(entry.getValue());
        }
        return res;
    }

    // 定义dfs(i, j) 表示当前可以选的下标集合为 i, 上一个选的数的下标是j,
    public int dfs(int i, int j){
        if(i == 0) return 1;
        if(cache[i][j] >= 0) return cache[i][j];
        int res = 0;
        for(int k = 0; k < n; k++){
            if(((i >> k) & 1) == 1 && isSqrt(nums[j] + nums[k])){
                res += dfs(i ^ (1 << k), k);
            }
        }
        return cache[i][j] = res;
    }

    public boolean isSqrt(int x){
        int i = (int)Math.sqrt(x);
        return i * i == x;
    }

    public int getFactorial(int x){
        int cnt = 1;
        for(int i = 1; i <= x; i++){
            cnt *= i;
        }
        return cnt;
    }
}

记忆化搜索转递推

class Solution {
    public int numSquarefulPerms(int[] nums) {
        int n = nums.length;
        int[][] f = new int[1 << n][n];
        for(int i = 0; i < n; i++)
            f[0][i] = 1;

        for(int i = 0; i < (1 << n); i++){
            for(int j = 0; j < n; j++){
                for(int k = 0; k < n; k++){
                    if(((i >> k) & 1) == 1 && isSqrt(nums[j] + nums[k]))
                        f[i][j] += f[i ^ (1 << k)][k];
                }
            }
        }
        int res = 0;
        for(int i = 0; i < n; i++) res += f[((1<<n)-1) ^ (1<<i)][i];
        Map<Integer, Integer> map = new HashMap<>();
        for(int num : nums) map.put(num, map.getOrDefault(num, 0) + 1);
        for(Map.Entry<Integer, Integer> entry : map.entrySet()){
            res /= getFactorial(entry.getValue());
        }
        return res;
    }

    public boolean isSqrt(int x){
        int i = (int)Math.sqrt(x);
        return i * i == x;
    }

    public int getFactorial(int x){
        int cnt = 1;
        for(int i = 1; i <= x; i++){
            cnt *= i;
        }
        return cnt;
    }
}

1879. 两个数组最小的异或值之和

难度困难36

给你两个整数数组 nums1 和 nums2 ，它们长度都为 n 。

两个数组的 异或值之和 为 (nums1[0] XOR nums2[0]) + (nums1[1] XOR nums2[1]) + ... + (nums1[n - 1] XOR nums2[n - 1]) （下标从 0 开始）。

比方说，[1,2,3] 和 [3,2,1] 的 异或值之和 等于 (1 XOR 3) + (2 XOR 2) + (3 XOR 1) = 2 + 0 + 2 = 4 。

请你将 nums2 中的元素重新排列，使得 异或值之和 最小。

请你返回重新排列之后的 异或值之和 。

示例 1：

输入：nums1 = [1,2], nums2 = [2,3]
输出：2
解释：将 nums2 重新排列得到 [3,2] 。
异或值之和为 (1 XOR 3) + (2 XOR 2) = 2 + 0 = 2 。

示例 2：

输入：nums1 = [1,0,3], nums2 = [5,3,4]
输出：8
解释：将 nums2 重新排列得到 [5,4,3] 。
异或值之和为 (1 XOR 5) + (0 XOR 4) + (3 XOR 3) = 4 + 4 + 0 = 8 。

提示：

n == nums1.length
n == nums2.length
1 <= n <= 14
0 <= nums1[i], nums2[i] <= 107

https://leetcode.cn/problems/minimum-xor-sum-of-two-arrays/solution/python-zhuang-tai-ya-suo-ji-yi-hua-sou-s-ih5w/

状态压缩 + 记忆化搜索

依次固定 nums1 中的待异或的元素，用 i 表示

搜索 nums2 中还未使用过的元素，方法是用 mask 表示，如果 mask 的第 j 位是 0 ，那 nums2[j] 未被使用过，把它与 nums1[i] 异或，然后继续 dfs

class Solution {
    int[][] cache;
    int[] nums1, nums2;
    public int minimumXORSum(int[] nums1, int[] nums2) {
        this.nums1 = nums1;
        this.nums2 = nums2;
        int n = nums1.length;
        cache = new int[n][1 << n];
        for(int i = 0; i < n; i++)
            Arrays.fill(cache[i], -1);
        return dfs(0, 0);
    }
	// 定义dfs(i,mask)表示，当前已经匹配了i个数，匹配的数在集合mask中，得到的最小异或值之和
    public int dfs(int i, int mask){
        if(i == nums2.length)
            return 0; // 递归终点: i == len(num)，说明num1和nums2中的每个数都异或过了
        if(cache[i][mask] >= 0) return cache[i][mask];
        int res = Integer.MAX_VALUE;
        for(int j = 0; j < nums2.length; j++){
            if(((1 << j) & mask) == 0){ // 如果 nums2[j] 未被使用过
                res = Math.min(res, (nums1[i] ^ nums2[j]) + dfs(i+1, mask | (1 << j)));
            }
        }
        return cache[i][mask] = res;
    }
}

状压DP

数据范围1-14优先考虑状压。

https://leetcode.cn/problems/minimum-xor-sum-of-two-arrays/solution/1879-liang-ge-shu-zu-zui-xiao-de-yi-huo-gats9/

class Solution {
    // 两个数组的最小异或值之和取决于两个数组的其中 n−1 对整数的异或值之和与剩余一对整数的异或值之和，
    // 因此可以使用动态规划计算两个数组的最小异或值之和。
    public int minimumXORSum(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int[] dp = new int[1 << n];
        // 二进制整数 i 表示数组 nums2 的前缀包含的数字的下标集合，将二进制整数 i 中的 1 的个数记为 count，
        // 则 dp[i] 表示数组 nums1 的前 count 个整数与
        //              数组 nums2 的特定 count 个整数（这些整数的下标集合由i表示）的最小异或值之和。
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0; // i=0 时，前缀为空，异或值之和一定为0
        for(int i = 1; i < (1 << n); i++){ // i 表示数组nums2的特定排列的前 count 个整数的集合。
            //则数组 nums 2的该特定排列的前 prevCount 个整数的集合是 i - 2^j
            int prevCount = Integer.bitCount(i) - 1;
            for(int j = 0; j < n; j++){
                if(((1 << j) & i) != 0){
                    dp[i] = Math.min(dp[i], dp[i - (1 << j)] + (nums1[prevCount] ^ nums2[j]));
                }
            }
        }
        return dp[(1 << n) - 1];
    }
}

1125. 最小的必要团队

难度困难177

作为项目经理，你规划了一份需求的技能清单 req_skills，并打算从备选人员名单 people 中选出些人组成一个「必要团队」（编号为 i 的备选人员 people[i] 含有一份该备选人员掌握的技能列表）。

所谓「必要团队」，就是在这个团队中，对于所需求的技能列表 req_skills 中列出的每项技能，团队中至少有一名成员已经掌握。可以用每个人的编号来表示团队中的成员：

例如，团队 team = [0, 1, 3] 表示掌握技能分别为 people[0]，people[1]，和 people[3] 的备选人员。

请你返回任一规模最小的必要团队，团队成员用人员编号表示。你可以按 任意顺序 返回答案，题目数据保证答案存在。

示例 1：

输入：req_skills = ["java","nodejs","reactjs"], people = [["java"],["nodejs"],["nodejs","reactjs"]]
输出：[0,2]

示例 2：

输入：req_skills = ["algorithms","math","java","reactjs","csharp","aws"], people = [["algorithms","math","java"],["algorithms","math","reactjs"],["java","csharp","aws"],["reactjs","csharp"],["csharp","math"],["aws","java"]]
输出：[1,2]

提示：

1 <= req_skills.length <= 16
1 <= req_skills[i].length <= 16
req_skills[i] 由小写英文字母组成
req_skills 中的所有字符串 互不相同
1 <= people.length <= 60
0 <= people[i].length <= 16
1 <= people[i][j].length <= 16
people[i][j] 由小写英文字母组成
people[i] 中的所有字符串 互不相同
people[i] 中的每个技能是 req_skills 中的技能
题目数据保证「必要团队」一定存在

题解：https://leetcode.cn/problems/smallest-sufficient-team/solution/zhuang-ya-0-1-bei-bao-cha-biao-fa-vs-shu-qode/

class Solution {
    // 把people堪称物品（集合），reqskills看成背包容量（目标集合），本题就是集合版的0-1背包问题
    // 状态压缩：为了方便计算，把reqskill的每个字符串映射到下标上，然后把每个people[i]映射转换成数字集合，再压缩成二进制数
    // 本题用到的位运算技巧：
    //     1.将元素x变为集合{x} : 1 << x
    //     2.判断元素x是否在集合A中 ： ((A >> x) & 1) == 1
    //     3.计算两个集合 A,B 的并集 A : A | B
    //     4.A\B在集合A中去掉集合B的元素 : A & ~B
    //     5.全集U : (1 << n) - 1
    private long all;
    private int[] mask; // mask[i] 记录 people[i] 拥有的技能
    private long[][] cache;
    public int[] smallestSufficientTeam(String[] req_skills, List<List<String>> people) {
        Map<String, Integer> sid = new HashMap<>();
        int m = req_skills.length;
        for(int i = 0; i < m; i++)
            sid.put(req_skills[i], i); // 将技能字符串映射到下标
        int n = people.size();
        mask = new int[n];
        for(int i = 0; i < n; i++){ // 把每个 people[i] 压缩成一个二进制数 mask[i]
            for(String s : people.get(i)){
                mask[i] |= (1 << sid.get(s));
            }
        }
        int u = 1 << m; // 需要的技能 全集
        cache = new long[n][u];
        for(int i = 0; i < n; i++){
            Arrays.fill(cache[i], -1);
        }
        all = (1L << n) - 1;
        long res = dfs(n-1, u-1);
        int[] ans = new int[Long.bitCount(res)];
        for(int i = 0, j = 0; i < n; i++){
            if(((res >> i) & 1) == 1)
                ans[j++] = i; // 所有在res中的下标
        }
        return ans;
    }

    // 定义dfs(i, j) 表示从前i个集合中选一些集合，并集包含j，至少需要选择的集合个数
    // 转移：
    //      不选第i个集合：dfs(i, j) = dfs(i-1, j)
    //      选第i个集合： dfs(i, j) = dfs(i-1, j \ people[i]) + 1
    //  两者取最小值
    // 递归边界： people集合i < 0 返回全集 ； 需要的技能集合j = 空集，返回空集
    // 递归入口：dfs(people集合, 需要的技能集合)
    public long dfs(int i, int j){
        if(j == 0) return 0; // 背包已装满
        if(i < 0) return all; // 没法装满背包，返回全集，这样下面比较集合大小会取更小的
        if(cache[i][j] >= 0) return cache[i][j];
        long res1 = dfs(i-1, j); // 不选mask[i]
        long res2 = dfs(i-1, j & ~mask[i]) | (1L << i); // 选 mask[i]
        return cache[i][j] = Long.bitCount(res1) < Long.bitCount(res2) ? res1 : res2;
    }
}

位运算练习题

78. 子集

难度中等2063

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

题解：假设nums=[1,2,3,4]，二进制的0可以写成0000，代表一个数也不取，1=0001表示去第一个数也就是[1]，2=0010，表示取第二个数[2]，3=0011表示取1和2位[1,2]，4=0100表示[3]…15=1111表示[1,2,3,4]

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        int n = nums.length;
        // 枚举集合（从空集到全集）
        for(int s = 0; s < (1 << n); s++){
            List<Integer> sub = new ArrayList<>();
            // 遍历集合
            for(int j = 0; j < n; j++){
                if(((s >> j) & 1) == 1) 
                    sub.add(nums[j]);
            }
            res.add(sub);
        }
        return res;
    }
}

77. 组合

难度中等1402

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

1 <= n <= 20
1 <= k <= n

方法二：Gosper’s Hack枚举所有大小为k的子集

class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        // Gosper's Hack
        for(int s = 0; s < (1 << n); s++){
            if(Integer.bitCount(s) == k){
                List<Integer> sub = new ArrayList<>();
                // 遍历集合
                for(int i = 0; i < n; i++){
                    if(((s >> i) & 1) == 1)
                        sub.add(i+1);
                }
                res.add(sub);
            }
        }
        return res;
    }
}

46. 全排列

难度中等2578

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同

回溯 + visit数组解法

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> cur = new ArrayList<>();
    boolean[] visit;
    public List<List<Integer>> permute(int[] nums) {
        visit = new boolean[nums.length];
        dfs(0, nums);
        return res;
    }

    public void dfs(int i, int[] nums){
        if(i == nums.length){
            res.add(new ArrayList<>(cur));
            return;
        }
        for(int k = 0; k < nums.length; k++){
            if(visit[k] == false){
                visit[k] = true;
                cur.add(nums[k]);
                dfs(i+1, nums);
                cur.remove(cur.size()-1);
                visit[k] = false;
            }
        }
    }

}

使用二进制枚举代替visit数组

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> cur = new ArrayList<>();
    int mask;
    public List<List<Integer>> permute(int[] nums) {
        mask = 0;
        dfs(0, nums);
        return res;
    }

    public void dfs(int i, int[] nums){
        if(i == nums.length){
            res.add(new ArrayList<>(cur));
            return;
        }
        for(int k = 0; k < nums.length; k++){
            if(((mask >> k) & 1) == 0){ // 没访问过
                mask |= (1 << k);
                cur.add(nums[k]);
                dfs(i+1, nums);
                cur.remove(cur.size()-1);
                mask ^= (1 << k);
            }
        }
    }
}