学习基础
神经网络的学习。这里所说的“学习”是指从训练数据中自动获取最优权重参数的过程。
神经网络的特征就是可以从数据中学习。所谓“从数据中学习”,是指可以由数据自动决定权重参数的值。
数据驱动
数据是机器学习的命根子。从数据中寻找答案、从数据中发现模式
机器学习的方法则极力避免人为介人,尝试从收集数据中发现答案(模式)。神经网络或深度学习则比以往的机器学习更加避免人为介人。
在实现数字“5”的识别问题中,神经网络直接学习图像本身,而在神经网络中,图像中包含的重要特征量也都是由机器来学习的。这里所说的“特征量”是指可以输入数据(输人图像)中准确地提取本质数据(重要的数据)的转换器。
深度学习有时也称为端到端机器学习。这里所说的端到端是指从一端到另一端的意思从**原始数据(输入)中获得目标结果(输出)**的意思。
训练数据和测试数据
机器学习中,一般将数据分为训练数据和测试数据两部分
首先,使用训练数据进行学习,寻找最优的参数
然后,使用测试数据评价训练得到的模型的实际能力。
之所以要将数据分为训练数据和测试数据,是因为追求的是模型的泛化能力。因此训练数据也可以称为监督数据
泛化能力是指处理未被观察过的数据(不包含在训练数据中的能力)。获得泛化能力是机器学习的最终目标。如果系统只能正确识别已有的训练数据,那有可能是只学习到了训练数据中的个人习惯写法。这样会导致可以顺利地处理某个数据集,但无法处理其他数据集的情况。此外,只对某个数据集过度拟合的状态称为过拟合(over fitting)。在机器学习中要尽量避免过拟合
损失函数
神经网络以某个指标为线索寻找最优权重参数。神经网络的学习中所用的指标称为损失函数。这个损失函数可以使用任意函数但一般用均方误差和交叉熵误差
损失函数是表示神经网络性能的“恶劣程度”的指标,即当前的神经网络对监督数据在多大程度上不拟合,在多大程度上不一致。如果给损失函数乘上一个负值,就可以解释为“在多大程度上不坏”, 即“性能有多好”。
均方误差
均方误差如下式所示:
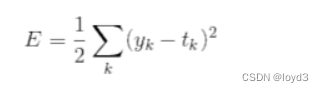
yk表示神经网络的输出,tk表示监督数据, k表示数据的维数
在手写数字识别的例子中,yk, tk是由如下10个元素构成的数据
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> t = [0,0,1,0,0,0,0,0,0,0]
神经网络的输出y时softmax函数的输出,softmax函数的输出可以理解为概率。t是监督数据,将正确解标签设为1,其他均设为0。这种将正确的标签表示为1,其他标签表示为0的表示方法称为one-hot表示。
用Python的实现如下:
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
交叉熵误差
交叉熵误差如下式所示:
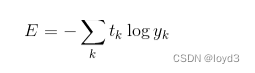
tk还是用one-hot表示
实际上上面式子只计算对应正确解标签的输出的自然对数。(错误解是0)
交叉熵误差的值是由正确解标签所对应的输出结果决定的
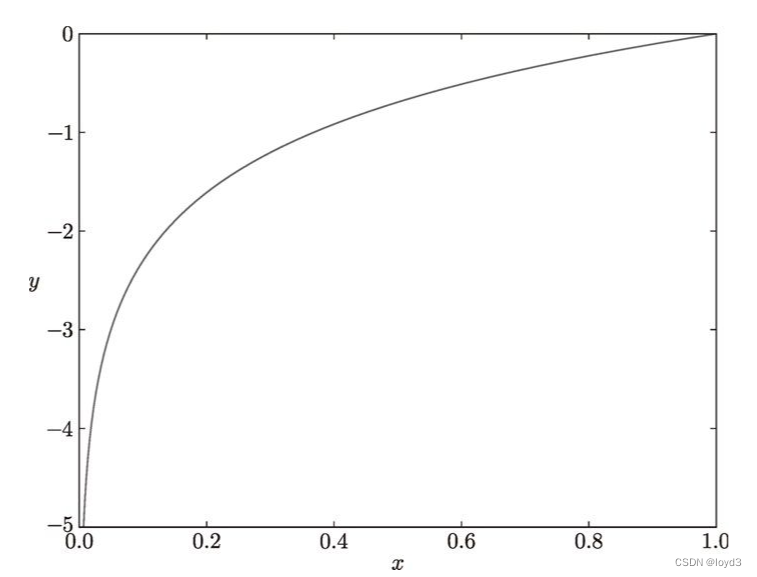
如图所示,x等于1时,y为0;随着x向0靠近,y逐渐变小,正确解标签对应的输出越大,公式的值越接近0; 当输出为1时,交叉熵误差为0。如果正确解标签对应的输出较小,则公式的值较大(误差越大)。
Python的实现如下
def cross_entropy_error(y,t):
delta=le-7
return -np.sum(t*np.log(y + delta))
这里加上了微小值delta,是因为当出现np.log(0)时,np.log(0)会变成负无穷大-inf,这样导致后面无法计算,为了避免出现这样的情况,所以添加这个微小值
为何要设定损失函数
这里有一个问题就是既然目标是为了获得精度尽可能高的神经网络,为什么不把识别精度作为指标,而要导入损失函数?
对于这一疑问,可以根据“导数”在神经网络学习中的作用来回答。在神经网络的学习中,寻找最优参数(权重和偏置)时,要寻找使损失函数的值尽可能小的参数。为了找到使损失函数的值尽可小的地方,需要计算参数的导数(确切地讲是梯度),然后以这个导数为指引逐步更新参数的值。
假设有一个神经网络,现在我们来关注这个神经网络中的某一个权重数。此时,对该权重参数的损失函数求导,表示的是“如果稍微改变这个权重参数的值,损失函数的值会如何变化”。如果导数的值为负,通过使该权重参数向正方向改变,可以减小损失函数的值;反过来,如果导数的值为正,则通过使该权重参数向负方向改变,可以减小损失函数的值。不过导数的值为0时,无论权重参数向哪个方向变化,损失函数的值都不会改时该权重参数的更新会停在此处。
之所以不能用识别精度作为指标,是因为这样一来绝大多数地方的导数都会变为0,导致参数无法更新。
为什么用识别精度作为指标时,参数的导数在绝大多数地方都会变为0?
那么看一个具体的例子:
假设某个神经网络正确识别出了100笔训练数据中的32笔,此时识别精度为32%。如果以识别精为指标,即使稍微改变权重参数的值,识别精度也仍将保持在32%,不会出现变化。也就是说,仅仅微调参数,是无法改善识别精度的。即便识别精度有所改善,它的值也不会像32.0123…%这样连续变化,而是变为33%,34%这样的不连续的、离散的值。
而如果把损失函数作为指标,则当前损函数的值可以表示为0.92543···这样的值。并且,如果稍微改变一下参数值,对应的损失函数也会像0.93432···这样发生连续性的变化。
识别精度对微小的参数变化基本上没有什么反应,即便有反应,它的值是不连续地、突然地变化。
作为激活函数的阶跃函数也有同样的情况。出于相同的原因,如果使用阶跃函数作为激活函数,神经网络的学习将无法进行。