【续上篇主成分分析】
因子分析常用于通过可观测变量推断出其背后的公共因子(也称为隐变量),样本在公共因子上的取值变化影响其在可观测变量上的取值,因为一般公共因子的个数小于可观测变量的数目,所以因子分析也可以用来降维。
对于下面三张表在主成分分析中已有详细的介绍,其中第三张表是因子载荷阵,是用标准化的主成分(公共因子)近似表示标准化原始变量的系数矩阵。如果用F1、F2表示各公共因子,以X1为例,可得:
![]()
| 表1 公因子方差 | ||
| 初始 | 提取 | |
| VAR1 | 1.000 | .836 |
| VAR2 | 1.000 | .842 |
| VAR3 | 1.000 | .856 |
| VAR4 | 1.000 | .807 |
| VAR5 | 1.000 | .990 |
| VAR6 | 1.000 | .989 |
| VAR7 | 1.000 | .765 |
| VAR8 | 1.000 | .841 |
| VAR9 | 1.000 | .945 |
| VAR10 | 1.000 | .622 |
| VAR11 | 1.000 | .739 |
| VAR12 | 1.000 | .904 |
| 提取方法:主成分分析法。 | ||
表2 方差分析表
| 成分 | 初始特征值 | 提取载荷平方和 | 旋转载荷平方和 | ||||
| 总计 | 方差百分比 | 累积 % | 总计 | 方差百分比 | 累积 % | 总计 | |
| 1 | 4.031 | 33.591 | 33.591 | 4.031 | 33.591 | 33.591 | 3.957 |
| 2 | 3.930 | 32.746 | 66.337 | 3.930 | 32.746 | 66.337 | 3.914 |
| 3 | 2.175 | 18.122 | 84.459 | 2.175 | 18.122 | 84.459 | 2.264 |
| 4 | .973 | 8.108 | 92.567 | ||||
| 5 | .513 | 4.278 | 96.845 | ||||
| 6 | .210 | 1.749 | 98.594 | ||||
| 7 | .104 | .864 | 99.458 | ||||
| 8 | .041 | .338 | 99.795 | ||||
| 9 | .024 | .202 | 99.998 | ||||
| 10 | .000 | .002 | 100.000 | ||||
| 11 | 5.402E-7 | 4.501E-6 | 100.000 | ||||
| 12 | -1.167E-16 | -9.728E-16 | 100.000 | ||||
| 表3 成分矩阵a | |||
| 成分 | |||
| 1 | 2 | 3 | |
| VAR1 | -.102 | -.030 | .908 |
| VAR2 | .836 | .084 | .368 |
| VAR3 | .782 | .353 | .345 |
| VAR4 | -.423 | -.070 | .790 |
| VAR5 | -.032 | -.991 | -.086 |
| VAR6 | .048 | .992 | .055 |
| VAR7 | -.632 | .604 | -.036 |
| VAR8 | -.550 | -.732 | .060 |
| VAR9 | .889 | .390 | -.040 |
| VAR10 | -.132 | .433 | -.646 |
| VAR11 | -.648 | .547 | .141 |
| VAR12 | .773 | -.536 | -.135 |
| 提取方法:主成分分析法。a | |||
| a. 提取了 3 个成分。 | |||
| 表4 成分得分系数矩阵 | |||
| 成分 | |||
| 1 | 2 | 3 | |
| VAR1 | -.025 | -.008 | .418 |
| VAR2 | .208 | .021 | .169 |
| VAR3 | .194 | .090 | .159 |
| VAR4 | -.105 | -.018 | .363 |
| VAR5 | -.008 | -.252 | -.040 |
| VAR6 | .012 | .252 | .025 |
| VAR7 | -.157 | .154 | -.016 |
| VAR8 | -.136 | -.186 | .028 |
| VAR9 | .221 | .099 | -.018 |
| VAR10 | -.033 | .110 | -.297 |
| VAR11 | -.161 | .139 | .065 |
| VAR12 | .192 | -.136 | -.062 |
| 提取方法:主成分分析法。 | |||
表4是因子得分系数矩阵,是用标准化原始变量表示标准化主成分(公共因子)的系数矩阵。由该得分系数矩阵可得两个公共因子关于标准化原始变量的线性表达式分别为:
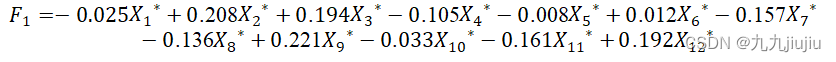
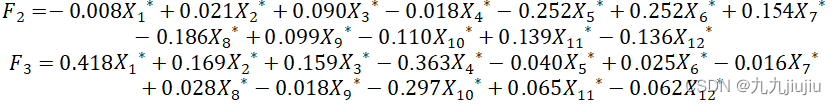
此外,由主成分法求解公共因子时,因子得分系数与因子载荷之间存在密切联系。如表中因子得分系数矩阵中的第一个元素为-0.025,它等于因子载荷阵的第一个元素-0.102除以第一主成分的方差4.031。之所以是除以方差而非标准差,是因为公共因子是标准化的主成分。同理,有-0.008=-0.03/3.93。由于用主成分法做因子分析中计算因子载荷阵和主成分分析中计算主成分的系数矩阵的方法本质上是一致的,两者的结果可以互相推导得到。因此,有些研究者也使用采用主成分法做因子分析得到的结果进行主成分分析。
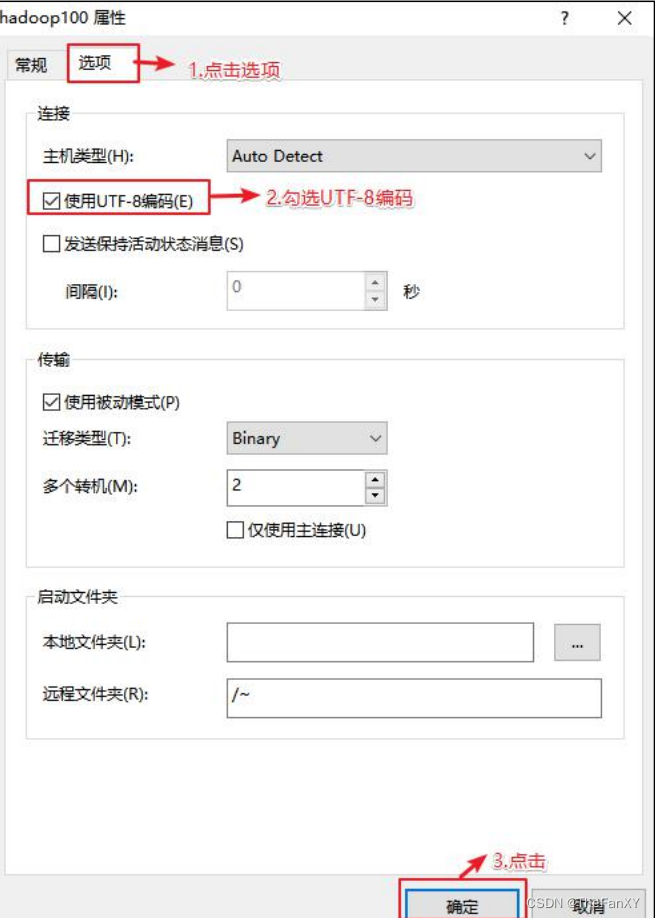
在进行因子分析之前,先了解变量之间的相关性,以判断是否适合对数据做因子分析。对此,进入“因子分析”对话框后,点击“描述”按钮,打开相应的对话框,在“统计”框架中可以选择“单变量”,将会输出每个变量的均值、方差等统计量的值。在下面“相关矩阵”框架中,选中“系数”选项以输出原始变量的相关阵,选中“显著水平”以输出原始变量各相关系数的显著性水平,选中 KMO and Bartlett ' s test of sphericity 以进行 KMO 检验和 Bartlett 球形检验。点击“确定”运行,可得到关于自变量相关性的检验结果,见输出结果。
其中, KMO 检验用于检查变量间的相关性和偏相关性, KMO 统计量的取值在0~1之间。 KMO 统计量的取值越接近于1,表明变量间的相关性越强,偏相关性越弱,因子分析的效果越好。实际分析中,当 KMO 统计量在0.7以上时,认为做因子分析的效果比较好;当 KMO 统计量在0.5以下时,不适合做因子分析,应考虑重新选取变量或者采用其他分析方法。如果变量间相互独立,则无法从中提取公因子,也就无法应用因子分析法。 Bartlett 球形检验的原假是相关阵为单位阵。如果拒绝原假设,则说明各变量间具有相关性,因子分析有效;如果不拒绝原假设,则说明变量间相互独立,不适合做因子分析。
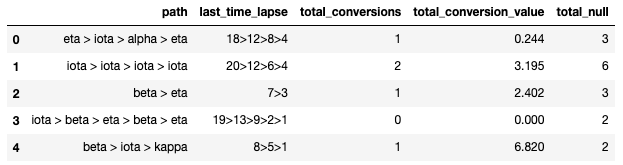
| 表5 相关性矩阵a | ||||||||||||
| VAR1 | VAR2 | VAR3 | VAR4 | VAR5 | VAR6 | VAR7 | VAR8 | VAR9 | VAR10 | VAR11 | VAR12 | |
| VAR1 | 1 | 0.244 | 0.18 | 0.807 | -0.023 | -0.009 | 0.023 | 0.107 | -0.118 | -0.359 | 0.097 | -0.155 |
| VAR2 | 0.244 | 1 | 0.861 | -0.195 | -0.138 | 0.145 | -0.548 | -0.39 | 0.686 | -0.294 | -0.35 | 0.461 |
| VAR3 | 0.18 | 0.861 | 1 | -0.185 | -0.402 | 0.408 | -0.367 | -0.557 | 0.751 | -0.195 | -0.167 | 0.281 |
| VAR4 | 0.807 | -0.195 | -0.185 | 1 | 0.027 | -0.067 | 0.318 | 0.179 | -0.351 | -0.403 | 0.176 | -0.277 |
| VAR5 | -0.023 | -0.138 | -0.402 | 0.027 | 1 | -0.999 | -0.546 | 0.726 | -0.416 | -0.331 | -0.566 | 0.523 |
| VAR6 | -0.009 | 0.145 | 0.408 | -0.067 | -0.999 | 1 | 0.532 | -0.731 | 0.429 | 0.346 | 0.558 | -0.511 |
| VAR7 | 0.023 | -0.548 | -0.367 | 0.318 | -0.546 | 0.532 | 1 | -0.253 | -0.299 | 0.357 | 0.523 | -0.728 |
| VAR8 | 0.107 | -0.39 | -0.557 | 0.179 | 0.726 | -0.731 | -0.253 | 1 | -0.847 | -0.292 | 0.137 | -0.15 |
| VAR9 | -0.118 | 0.686 | 0.751 | -0.351 | -0.416 | 0.429 | -0.299 | -0.847 | 1 | 0.092 | -0.422 | 0.548 |
| VAR10 | -0.359 | -0.294 | -0.195 | -0.403 | -0.331 | 0.346 | 0.357 | -0.292 | 0.092 | 1 | 0.131 | -0.217 |
| VAR11 | 0.097 | -0.35 | -0.167 | 0.176 | -0.566 | 0.558 | 0.523 | 0.137 | -0.422 | 0.131 | 1 | -0.908 |
| VAR12 | -0.155 | 0.461 | 0.281 | -0.277 | 0.523 | -0.511 | -0.728 | -0.15 | 0.548 | -0.217 | -0.908 | 1 |
| a. 此矩阵不是正定矩阵。 | ||||||||||||
由上面第一张表的结果可以看到,12个变量之间部分变量存在较强的相关关系,适合进行主成分分析。另外,得到初始载荷矩阵与公共因子后,为了解释方便,往往需要对因子进行旋转,因此在上述设置的基础上,在主对话框中点击右侧的“旋转”按钮,在“方法”框架中可以看到 SPSS 给出了多种旋转方法。可以选择的方法有 Varimax (方差最大正交旋转)、 Direct Oblimin (直接斜交旋转)、 Quartimax (四次方最大正交旋转)、 Equamax (等量最大正交旋转)及 Promax (最优斜交旋转)。系统默认为不进行旋转,此处选择方差最大正交旋转,“显示”框架中“旋转结果”选项处于活动状态,选中该选项以输出旋转结果。点击“确定”运行,得到输出结果。
| 表6 旋转后的成分矩阵a | |||
| 成分 | |||
| 1 | 2 | 3 | |
| VAR1 | .101 | .095 | .904 |
| VAR2 | -.405 | .789 | .234 |
| VAR3 | -.159 | .895 | .171 |
| VAR4 | .251 | -.207 | .837 |
| VAR5 | -.780 | -.610 | .100 |
| VAR6 | .768 | .617 | -.133 |
| VAR7 | .857 | -.163 | -.063 |
| VAR8 | -.254 | -.841 | .263 |
| VAR9 | -.221 | .919 | -.225 |
| VAR10 | .380 | .006 | -.691 |
| VAR11 | .834 | -.170 | .122 |
| VAR12 | -.899 | .277 | -.134 |
| 提取方法:主成分分析法。 旋转方法:凯撒正态化最大方差法。a | |||
| a. 旋转在 5 次迭代后已收敛。 | |||
| 表7 成分转换矩阵 | |||
| 成分 | 1 | 2 | 3 |
| 1 | -.596 | .793 | -.130 |
| 2 | .800 | .572 | -.182 |
| 3 | .070 | .212 | .975 |
| 提取方法:主成分分析法。 旋转方法:凯撒正态化最大方差法。 | |||
| 表8 成分得分系数矩阵 | |||
| 成分 | |||
| 1 | 2 | 3 | |
| VAR1 | .038 | .064 | .412 |
| VAR2 | -.095 | .213 | .134 |
| VAR3 | -.033 | .239 | .113 |
| VAR4 | .074 | -.016 | .371 |
| VAR5 | -.200 | -.159 | .008 |
| VAR6 | .196 | .159 | -.023 |
| VAR7 | .215 | -.040 | -.024 |
| VAR8 | -.066 | -.209 | .079 |
| VAR9 | -.053 | .228 | -.065 |
| VAR10 | .087 | -.026 | -.305 |
| VAR11 | .212 | -.034 | .059 |
| VAR12 | -.228 | .061 | -.061 |
| 提取方法:主成分分析法。 旋转方法:凯撒正态化最大方差法。 | |||

由输出结果可以看到,旋转后公共因子解释原始数据的能力没有提高,但因子载荷矩阵及因子得分系数矩阵都发生了变化,因子载荷矩阵中的元素更倾向于0。有时为了使公共因子的实际意义更容易解释,往往需要放弃公共因子之间互不相关的约束而进行斜交旋转,最常用的斜交旋转方法为 Promax 方法,可得到输出结果。
| 模式矩阵a | |||
| 成分 | |||
| 1 | 2 | 3 | |
| VAR1 | .160 | .170 | .930 |
| VAR2 | -.401 | .829 | .278 |
| VAR3 | -.158 | .923 | .233 |
| VAR4 | .311 | -.146 | .847 |
| VAR5 | -.770 | -.583 | .019 |
| VAR6 | .757 | .588 | -.052 |
| VAR7 | .860 | -.197 | -.035 |
| VAR8 | -.228 | -.819 | .192 |
| VAR9 | -.247 | .916 | -.170 |
| VAR10 | .336 | -.065 | -.683 |
| VAR11 | .848 | -.187 | .151 |
| VAR12 | -.916 | .297 | -.159 |
| 提取方法:主成分分析法。 旋转方法:凯撒正态化最优斜交法。 | |||
| a. 旋转在 5 次迭代后已收敛。 | |||
| 结构矩阵 | |||
| 成分 | |||
| 1 | 2 | 3 | |
| VAR1 | .059 | .029 | .884 |
| VAR2 | -.389 | .763 | .192 |
| VAR3 | -.136 | .877 | .104 |
| VAR4 | .202 | -.265 | .833 |
| VAR5 | -.804 | -.628 | .204 |
| VAR6 | .795 | .637 | -.237 |
| VAR7 | .853 | -.144 | -.106 |
| VAR8 | -.296 | -.863 | .351 |
| VAR9 | -.177 | .930 | -.288 |
| VAR10 | .414 | .064 | -.713 |
| VAR11 | .820 | -.166 | .080 |
| VAR12 | -.881 | .272 | -.097 |
| 提取方法:主成分分析法。 旋转方法:凯撒正态化最优斜交法。 | |||
| 成分相关性矩阵 | |||
| 成分 | 1 | 2 | 3 |
| 1 | 1.000 | .054 | -.119 |
| 2 | .054 | 1.000 | -.161 |
| 3 | -.119 | -.161 | 1.000 |
| 提取方法:主成分分析法。 旋转方法:凯撒正态化最优斜交法。 | |||
可以看到与正交旋转不同,斜交旋转的输出结果中没有Rotated Component Matrix,而代之以 Pattern Matrix 和 Structure Matrix 。这里,Pattern Matrix 即因于载荷矩阵,而 Structure Matrix 为公共因子与标准化原始变量的相关阵。也就是说,在斜交旋转中,因子载荷系数不再等于公共因子与标准化原始变量的相关系数。
由 Pattern Matrix 可知,变量X5、X6、X7、X11、X12在第一公共因子上的载荷均较大,因此第一公共因子主要反映第二、三产业就业结构、产业劳动生产率;变量X2、X3、X8、X9在第二公共因子上的载荷较大,则第二公共因子主要反映第二、三从业人员、产业产出结构;变量X1、X4、X10在第三公共因子上的载荷较大,则第三公共因子主要反映第一产业相关情况。总之,三个公共因子均较未旋转前更容易解释。