1. 前言

归并排序算法是采用
分治法的一个经典案例
它和数据结构中的二叉树有异曲同工之妙
我们将从如何合并两个有序数组
到如何递归自身达到有序两个方面
给大家介绍归并排序的递归版本

在这里插入图片描述

准备好,大家上车开启归并之旅
(注意:本章排序都按升序讲解)

2. 归并排序基本思路

我们先创建一个无序数组:

int a[]={10,6,7,1,3,9,4,2};

基本思路:

拆分过程:

要使数组整体有序就要将
左半部分和右半部分变为有序
后进行单次归并排序
将数组拆分为两个部分A和B
要使A数组有序就要将
A也拆分为两个部分
使左/右半部分都有序
一直拆分直到数组只有一个元素

画图理解:

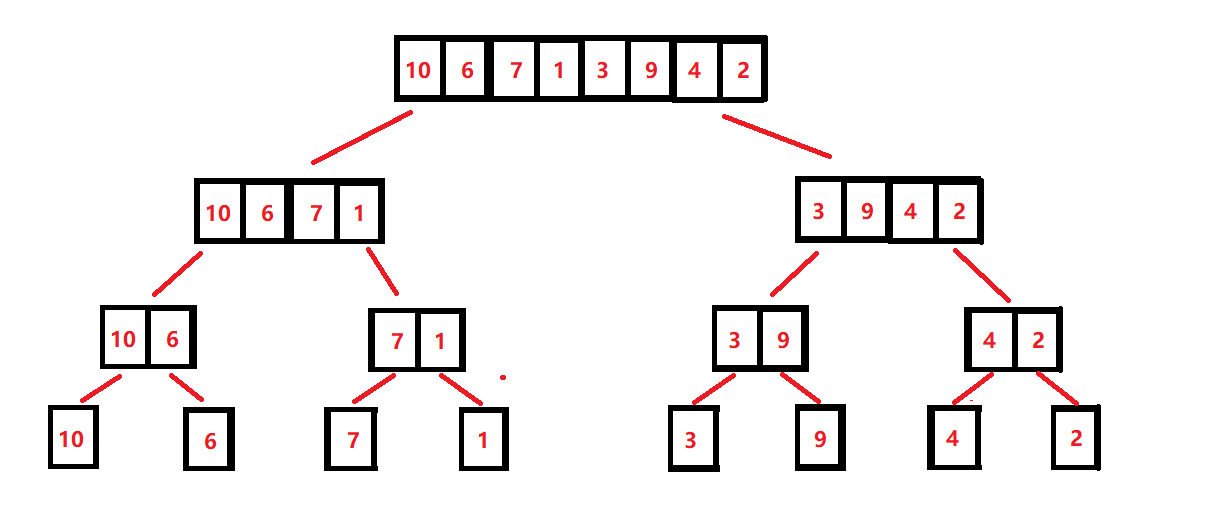
在这里插入图片描述

合并过程:

从左往右将6,10合并为有序
将7,1合并为有序后6,10,7,1再合并
数组的左半部分有序后.走右边
将3,9合并为有序后将4,2合并为有序
再将3.9.4.2合并为有序
至此左右子区间都有序
再将左右子区间归并为有序
使数组整体有序

画图理解:

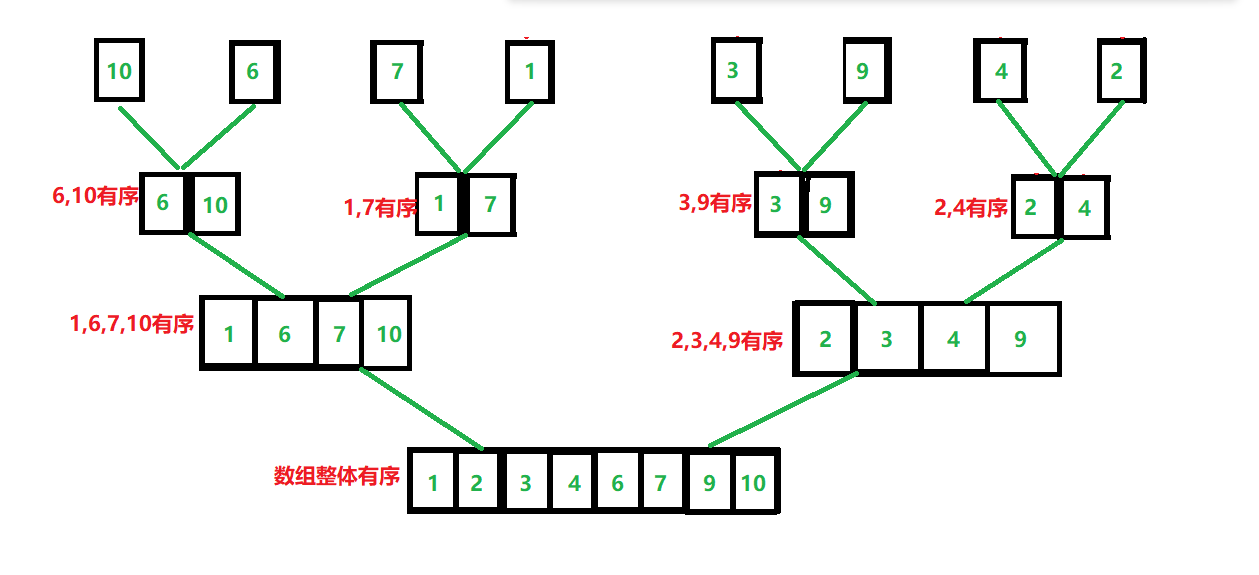
在这里插入图片描述

这里给大家放出一个动图
帮助大家理解这个过程:

归并排序

3. 对合并两个有序数组的思考

我们由易到难,定义两个有序数组:

int a[]={1,2,3};
int b[]={2,5,6};

方法:

定义两个指针A和B
分别指向两个数组的第一个元素
定义一个数组C接收这两个数组的数据
A和B指向的值谁小,谁就放在C中第一个位置
然后对应的指针(A或B)往后走一步
直到走完其中一个数组后停下来

画图理解:

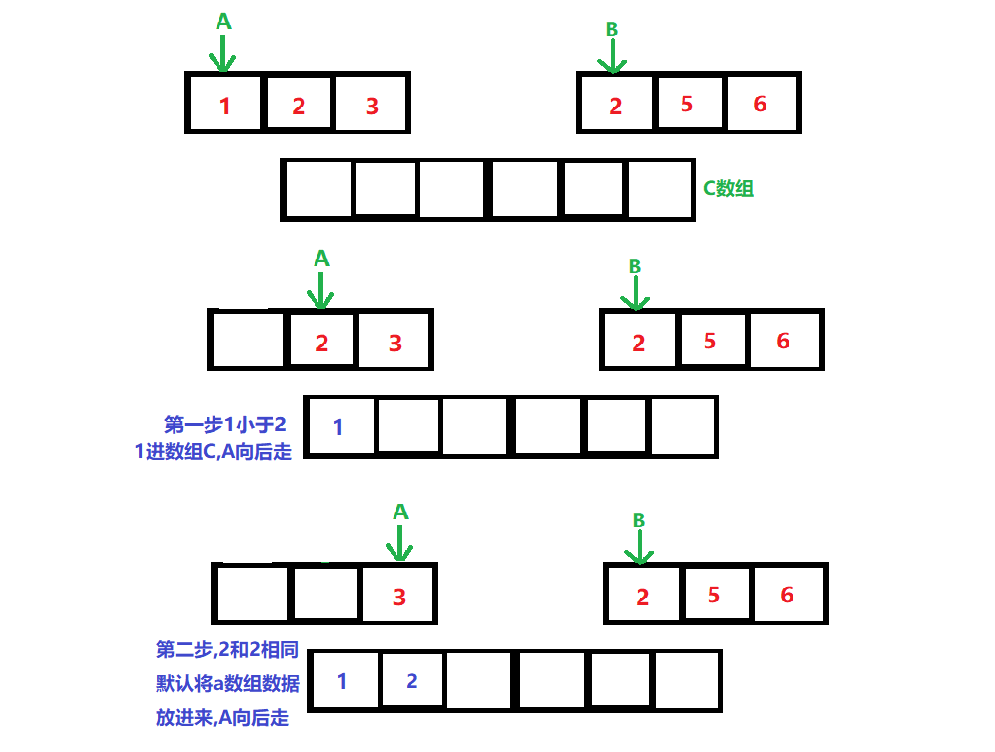
在这里插入图片描述

像这样往后一直走
这里我给出力扣平台的动图视频
帮助大家理解:

合并两个有序数组

4. 合并两个有序数组代码实现

我们刚刚说明了
合并两个有序数组
在原数组中不好操作
所以我们定义一个临时数组tmp
来接收排序好的顺序,最后再拷贝回原数组

while (begin1 < end1 && begin2 < end2)//begin指针指向两个有序数组的第一个元素.end为数组有效范围
	{
		if (a[begin1] < a[begin2])//谁小谁就先进tmp数组
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	while (begin1 < end1)//当其中一个数组走完后.将另外一个数组所有内容直接放进tmp数组
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 < end2)//数组1先走完就将数组2剩下全部内容放进去
	{
		tmp[i++] = a[begin2++];
	}
	//将tmp数组的内容拷贝回a数组
	for (int j = left; j < right; j++)
	{
		a[j] = tmp[j];
	}
}

5. 归并排序递归版代码实现

由于每次都需要二分数组
而且需要为临时数组tmp开辟空间
在原函数上直接递归就不太方便
所以我们设计一个主函数和一个递归函数
方便我们编写代码

主函数:

//归并排序
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);//为临时数组tmp开辟空间
	if (tmp == NULL)
	{
		printf("动态开辟失败");
		exit(-1);
	}
	_MergeSort(a, 0, n - 1, tmp);//_MergeSort为递归函数.传参进行递归过程
	free(tmp);
	tmp = NULL;
}

递归函数:

//归并排序的子程序
void _MergeSort(int* a, int left, int right, int* tmp)
{
	if (left >= right)
	{
		return;
	}
	int mid = (left + right) / 2;
	_MergeSort(a, left, mid, tmp);//进了函数一直递归,直到数组元素为1个后开始归并排序
	_MergeSort(a, mid + 1, right, tmp);//先递归左边再递归右边

	int begin1 = left;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = right;
	int i = left;
	while (begin1 < end1 && begin2 < end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	while (begin1 < end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 < end2)
	{
		tmp[i++] = a[begin2++];
	}
	//将tmp数组的内容拷贝回a数组
	for (int j = left; j < right; j++)
	{
		a[j] = tmp[j];
	}

}