有理函数积分,一共分为三步:
①有理函数拆分
②求待定系数
③积分
一、有理函数拆分
有理函数拆分就是需要把被积函数拆开成若干项简单真分式相加。
(真分式:分子最高次幂<分母最高次幂)
简单真分式,指的是
1
(
x
−
A
)
p
\frac{1}{(x-A)^p}
(x−A)p1和
1
(
x
2
+
M
x
+
N
)
q
\frac{1}{(x^2+Mx+N)^q}
(x2+Mx+N)q1类型的分式,其中,
x
2
+
M
x
+
N
x^2+Mx+N
x2+Mx+N在实数范围内不能因式分解。
有理函数拆分步骤
1.确保有理函数是真分式,如果有理函数不是真分式,需要把它拆分成多项式和真分式之和。假设
R
(
x
)
P
(
x
)
=
R
1
(
x
)
+
r
(
x
)
P
(
x
)
\frac{R(x)}{P(x)}=R_1(x)+\frac{r(x)}{P(x)}
P(x)R(x)=R1(x)+P(x)r(x),其中
r
(
x
)
P
(
x
)
\frac{r(x)}{P(x)}
P(x)r(x)为真分式,然后继续对
r
(
x
)
P
(
x
)
\frac{r(x)}{P(x)}
P(x)r(x)进行拆分。
2.在实数范围内分母因式分解彻底,设为
r
(
x
)
P
(
x
)
=
r
(
x
)
(
x
−
A
)
p
(
x
2
+
M
x
+
N
)
q
\frac{r(x)}{P(x)}=\frac{r(x)}{(x-A)^p(x^2+Mx+N)^q}
P(x)r(x)=(x−A)p(x2+Mx+N)qr(x)
3.拆分.
r
(
x
)
(
x
−
A
)
p
(
x
2
+
M
x
+
N
)
q
\frac{r(x)}{(x-A)^p(x^2+Mx+N)^q}
(x−A)p(x2+Mx+N)qr(x)
=
a
1
x
−
A
+
a
2
(
x
−
A
)
2
+
.
.
.
+
a
p
(
x
−
A
)
p
+
b
1
x
+
c
1
x
2
+
M
x
+
N
+
b
2
x
+
c
2
(
x
2
+
M
x
+
N
)
2
+
.
.
.
+
b
q
x
+
c
q
(
x
2
+
M
x
+
N
)
q
=\frac{a_1}{x-A}+\frac{a_2}{(x-A)^2}+...+\frac{a_p}{(x-A)^p}+\frac{b_1x+c_1}{x^2+Mx+N}+\frac{b_2x+c_2}{(x^2+Mx+N)^2}+...+\frac{b_qx+c_q}{(x^2+Mx+N)^q}
=x−Aa1+(x−A)2a2+...+(x−A)pap+x2+Mx+Nb1x+c1+(x2+Mx+N)2b2x+c2+...+(x2+Mx+N)qbqx+cq
下面举两个简单的例子:

下面再举两个例子:


二、求待定系数
有理函数会拆分了,接下来需要把待定系数求出来,主要有如下几个方法:
①构造方程组法.通分化简,相同次幂的系数相同,构造方程组,解出待定系数。
②留数法.等式两边同时乘以某个因子,再令该因子为零,解出待定系数。
③极限法.如果已经求得几个待定系数,可以用对x取极限的方法求得剩余待定系数。
④特殊值法.如果已经求得几个待定系数,可以用对x取特殊值的方法求得剩余待定系数。
我们从易到难,进行举例。

将此真分式拆分成:

我们可以利用构造方程组法,将等式右边进行通分,根据待定系数法求出a,b,c。
但显然这个方法有点繁琐,所以我们用留数法。
什么是留数法呢?
以上述为例,先将等式两边同时乘以(x-1),然后右边就得到了a+==(x-1)(含b,c因子)==这时,直接令x=1,等式右边就只是留下了a,进而解出a。
同理,解出b和c。

解出a,b和c之后,就可以很快做出来这道题目了。

接下来我们看这道题目。

首先还是要进行拆分,这是一个真分式,而且分母也已经是最简形式了。

拆分之后,接下来我们需要解出a,b,c。
同样,我们使用留数法。
对于a,我们等式两边同时乘以x,然后令x=0,解出a。
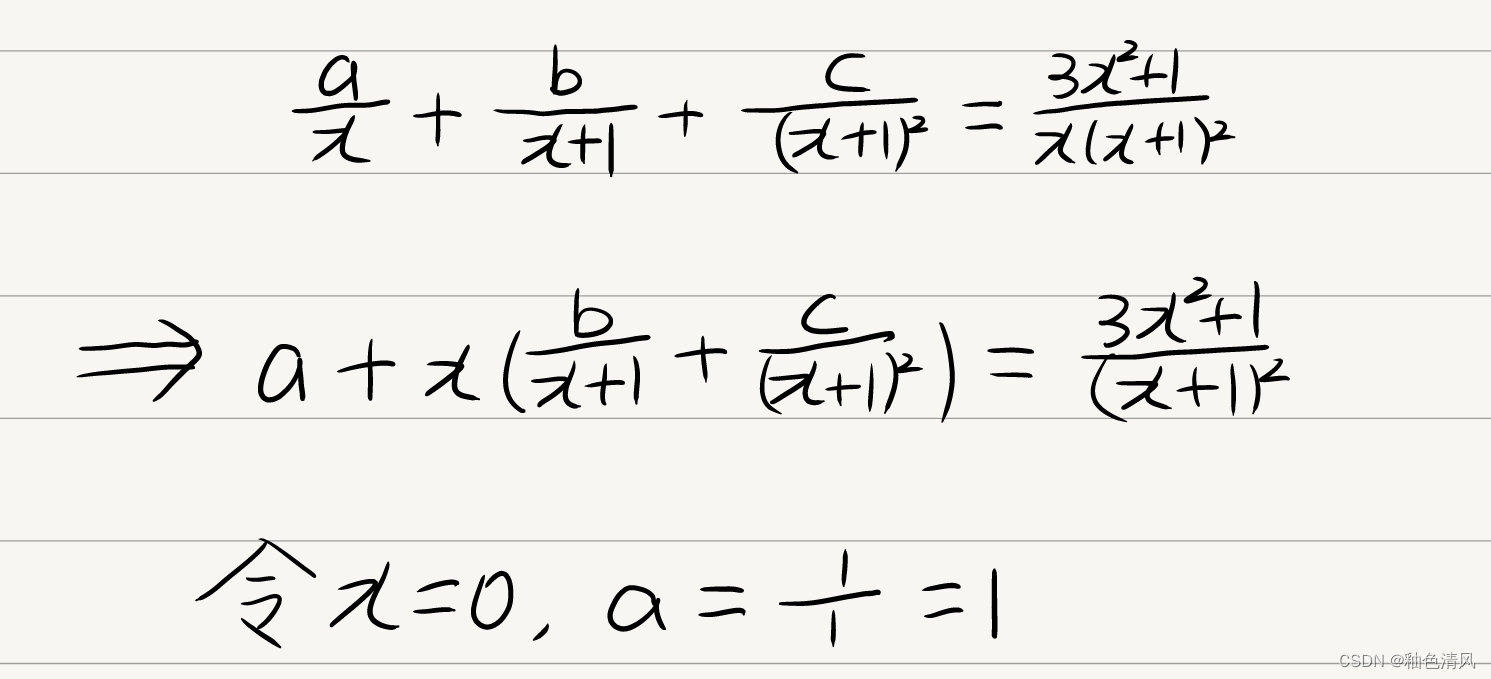
我们如同上述,解出b,等式两边同时乘以(x+1)

但是此时这样做就有问题了!等式右边会出现无穷大的情况。
为什么会出现这种情况呢,这是因为有
c
(
x
+
1
2
)
\frac{c}{(x+1^2)}
(x+12)c。
遇到这类情况我们一般要先解决分母次数更高的那一项。对于这道题,即先解出c。

这时,只剩下b这个未知数了,我们可以利用特殊值法,将x=1代入等式,解出b。

在这里,我们也可以使用取极限法,如下。

接下来,我们看下一个例子。

首先初步判断,这是一个假分式,我们需要将其进行拆分成一个x的多项式+一个真分式。

对于x的积分,我们是清楚的,主要要解决第二项这个真分式。
注意到它的分母是可以进一步化简的,因此:
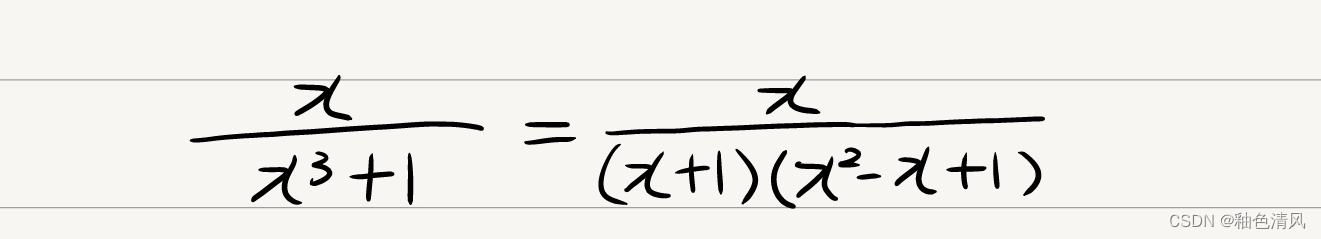
然后,我们要进行下一步的拆分。

拆分之后,我们需要解出a,b,c。
对于a来说,根据留数法,是很容易解出来的。

但是对于bx+c,我们能否根据留数法解出来呢?注意到,
x
2
−
x
+
1
x^2-x+1
x2−x+1是恒大于0的。它无法使得出它之外的其他项(即有a的那一项)变为0的。
这时我们使用极限法。

解出a,b对于c我们可以根据特殊值法解出c。

总结:
①若因子
1
(
x
−
A
)
p
\frac{1}{(x-A)^p}
(x−A)p1最高次幂的系数,p=1,可以直接用留数法。
②若因子
1
(
x
−
A
)
p
\frac{1}{(x-A)^p}
(x−A)p1其他次幂的系数,p=2,可以通过特殊值法或者极限法求得。
③因子
1
(
x
2
+
M
x
+
N
)
q
\frac{1}{(x^2+Mx+N)^q}
(x2+Mx+N)q1一般用特殊值法和极限法求得待定系数。
三、积分
求解出待定系数,然后就可以积分了。
以上述的例2和例3为例,完成上述例子。
例2:

例三: