1. 差分进化算法简介
（以下描述，均不是学术用语，仅供大家快乐的阅读）
差分进化算法（Differential Evolution Algorithm，DE）是一种基于群体的进化算法，它模拟了群体中的个体的合作与竞争的过程。算法原理简单，控制参数少，只有交叉概率和缩放比例因子，鲁棒性强，易于实现。
差分进化算法中，每一个个体的基因表示待求问题的一个候选解。每次迭代将先进行变异操作，选择一个或多个个体的基因作为基，然后选择不同的个体的差分来构成差分基因，最后将作为基的基因与差分基因相加来得出新的个体。交叉操作将新的个体将于父代的对应个体交叉，然后进行选择操作，比较交叉后的个体与父代的对应个体，选择较优的个体保留至下一代。在迭代完成之后将选择种群中最优个体的基因作为解。
差分进化算法可以算是我所使用过的优化算法中大魔王级别的算法，虽然它每个方面都没有强到离谱，但是综合起来的效果好于大多数算法。它就像一个每个科目都能考到90分（百分制）的学生，虽然没门课都不是最优秀的，但是论综合，论总分，它有极大的概率是第一名。
（两位（正经）魔王，一位宇宙帝王，一位蚁王，蚁王更符合差分进化算法，因为他可以不断的吞食其他个体并吸收他们的能力从而不断变强，是不是和优化算法很像？富坚老贼还是狠）
在我研究优化算法的小路上，我的目标就是找到一个能打败大魔王或是能在大多数方面压制魔王的算法。
2. 算法流程
这次的主角就选魔王军吧（或者蚁王军，为了与蚁群算法区别还是叫魔王军吧），个体则称之为魔王兵。
魔王兵的能力取决于它们的基因，它们可以根据环境或者需要改变自己的基因使得自己更加强大，更方便的处理问题，问题的维度与基因维度相同。
表示第i个魔王兵在进化了第t次后的基因，该个体有D位基因。
与遗传算法同为进化算法的差分进化算法，它们的操作（算子）也都非常相似的，都是交叉，变异和选择，流程也几乎一样（遗传算法先交叉后变异，差分进化算法先变异后交叉）。
2.1变异
说到差分进化算法中的变异，我就想到一句论语“三人行，必有我师焉。择其善者而从之，其不善者而改之。”，其实这句论语已经向我们说明了差分进化算法的整个流程：
“三人行，必有我师焉”——变异，交叉。
“择其善者而从之，其不善者而改之”——选择。
差分进化算法中，当一个魔王兵变异时，它会先找来3个小伙伴，当然是随机找来3个小伙伴，避免同化。在一个小伙伴的基因上加上另外两个小伙伴基因之差作为自己的目标基因。其变异公式如下：
表示第i个魔王兵找到了编号为r1、r2和r3的三个魔王兵，当然了i、r1、r2、r3为互不相同的整数，F为缩放比例因子，通常 ，一般取F=0.5。
为第i个魔王兵交叉后的目标基因图纸，不过这是个半成品，再经过交叉后，目标基因图纸才算完成。
其实现在我们已经有了5个基因图纸了
，接下来将进行交叉操作。由于变异操作，差分进化算法的种群中个体数至少为4，即魔王军中至少有4个小兵。
2.2交叉
交叉操作中，魔王兵i会将目标基因图纸
进行加工得到
，加工过程如下：
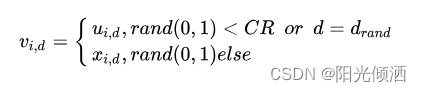
其中 。 为交叉概率，其值越大，发生交叉的概率越大，一般取 。
为{1,2,…,D}中的随机整数，其作用是保证交叉操作中至少有一维基因来自变异操作产生的基因，不能让交叉操作的努力白费。
从公式上可以看出交叉操作实际上是从变异操作得出的基因图纸上选择至少一位基因来替换自己的等位基因，得到最终的基因图纸。
2.3选择
选择操作相对简单，魔王兵i拿到了最终的基因图纸
，大喊一声，进化吧，魔王兵i的基因改变了。它拿出了能力测量器fitness function,如果发现自己变强了，那么就将基因 保留到下一代，否则它选择放弃进化，让自己还原成
。
3. 实验初步
实验又来啦，还是那个实验
，简单、易算、好画图。
实验1：参数如下
| 参数 | 值 |
| 问题维度(维度) | 2 |
| 小兵数量(种群数) | 20 |
| 进化次数(最大迭代次数) | 50 |
| CR（交叉率） | 0.3 |
| F（放缩因子） | 0.5 |
| 取值范围 | （-100，100） |
| 实验次数 | 10 |
图中可以看出在第20代时，群体已经非常集中了，在来看看最终得出的结果。
| 值 | |
| 最优值 | 1.0917867028293985E-8 |
| 最差值 | 2.9361020954274757E-6 |
| 平均值 | 5.847453820715603E-7 |
这结果真是好到令人发指，恶魔在心中低语“把其他的优化算法都丢掉吧”。不过别往心里去，任何算法都有优缺点，天下没有免费的午餐，要想获得某种能力必须付出至少相应的代价。
实验2：
将交叉率CR设为0,即每次交叉只选择保留一位变异基因。
| 参数 | 值 |
| 问题维度(维度) | 2 |
| 小兵数量(种群数) | 20 |
| 进化次数(最大迭代次数) | 50 |
| CR（交叉率） | 0.0 |
| F（放缩因子） | 0.5 |
| 取值范围 | （-100，100） |
| 实验次数 | 10 |
看看了看图，感觉跟实验1中相比没有什么变化，那我们再来看看结果。
| 值 | |
| 最优值 | 2.922699066690564E-10 |
| 最差值 | 1.5170095944418442E-7 |
| 平均值 | 1.9533094363773728E-8 |
结果总体来说比实验1好了一个数量级。为什么呢？个人感觉应该是每次只改变一位基因的局部搜索能力比改变多位基因更强。下面我们将交叉率CR设为1来看看是否是这样。
实验3：
将交叉率CR设为1,即每次交叉只选择保留一位原有基因。
| 参数 | 值 |
| 问题维度(维度) | 2 |
| 小兵数量(种群数) | 20 |
| 进化次数(最大迭代次数) | 50 |
| CR（交叉率） | 1.0 |
| F（放缩因子） | 0.5 |
| 取值范围 | （-100，100） |
| 实验次数 | 10 |
实验3的图与实验1和实验2相比好像也没什么差别,只是收敛速度好像快了那么一点点。再来看看结果。
| 值 | |
| 最优值 | 1.247729854010192E-10 |
| 最差值 | 2.3424955950460443E-8 |
| 平均值 | 4.089766498652818E-9 |
发现结果比实验2的结果还要好？那说明了实验2我得出的结论是可能是错误的，交叉率在该问题上对差分进化算法的影响不大，它们结果的差异可能只是运气的差异，毕竟是概率算法。
实验4：
将变异放缩因子设为0，即变异只与一个个体有关。
| 参数 | 值 |
| 问题维度(维度) | 2 |
| 小兵数量(种群数) | 20 |
| 进化次数(最大迭代次数) | 50 |
| CR（交叉率） | 0.3 |
| F（放缩因子） | 0.0 |
| 取值范围 | （-100，100） |
| 实验次数 | 10 |
收敛速度依然很快，不过怎么感觉结果不对，而且个体收敛的路径好像遗传算法，当F=0，时，差分进化算法退化为了没有变异、选择操作的遗传算法，结果一定不会太好。
| 值 | |
| 最优值 | 0.453120676982517 |
| 最差值 | 286.3408283178992 |
| 平均值 | 106.1719276191775 |
果然如此。下面我们再看看F=2时的实验。
实验5：
将变异放缩因子设为2。
| 参数 | 值 |
| 问题维度(维度) | 2 |
| 小兵数量(种群数) | 20 |
| 进化次数(最大迭代次数) | 50 |
| CR（交叉率） | 0.3 |
| F（放缩因子） | 2.0 |
| 取值范围 | （-100，100） |
| 实验次数 | 10 |
实验5的图可以明显看出，群体的收敛速度要慢了许多，到第50代时，种群还未完全收敛于一点，那么在50代时其结果也不会很好，毕竟算法还未收敛就停止进化了。
| 参数 | 值 |
| 最优值 | 0.003982238947037151 |
| 最差值 | 1.1517176365886543 |
| 平均值 | 0.23692008026134745 |
结果不算很好但也算相对稳定。
通过上面5个实验，我们大致了解了差分进化算法的两个参数的作用。
交叉率CR，影响基因取自变异基因的比例，由于至少要保留一位自己的基因和变异的基因导致CR在该问题上对算法性能的影响不大（这个问题比较简单，维度较低，影响不大）。
变异放缩因子F，影响群体的收敛速度，F越大收敛速度越慢，F绝对值越小收敛速度越快，当F=0是群体之间只会交换基因，不会变异基因。
4. 探究与改进
差分进化算法大魔王已经如此强大了，那么还有什么可以改进的呢？当然有下面一一道来。
方案1.将3人行修改为5人行，以及推广到2n+1人行。
实验6：
将3人行修改为5人行，变异公式如下：
| 参数 | 值 |
| 问题维度(维度) | 2 |
| 小兵数量(种群数) | 20 |
| 进化次数(最大迭代次数) | 50 |
| CR（交叉率） | 0.3 |
| F1（放缩因子） | 0.5 |
| F2（放缩因子） | 0.5 |
| 取值范围 | （-100，100） |
| 实验次数 | 10 |
五人行的实验图看起来好像与之前并没有太大的变化，我们再来看看结果。
| 参数 | 值 |
| 最优值 | 1.7892717650452213E-8 |
| 最差值 | 4.573249741855863E-6 |
| 平均值 | 1.0415260793972972E-6 |
结果没有明显提升，反而感觉比之前的结果差了。反思一下五人行的优缺点，优点，取值范围更大，缺点，情况太多，减慢搜索速度。
上图为（这里的公式不显示？）的情况，其中ABCD为平行四边形AD=DE，U可以取到AE上的任一点。
上图为 
（这里的公式不显示？）的情况，其中ABCD为平行四边形AD=DE，AFGH为平行四边形，AIJE为平行四边形，AH=HI, U可以取到平行四边形AIJE上的任一点。
对于交叉操作来所，“五人行”的选择更多，搜索能力应该更强，但这个问题的适应度函数过于简单，可能无法发挥其优势，所以此时“五人行”的结果差于“三人行”的结果。
方案2，变异放缩因子随机化
第3节中我们可以明显看出变异放缩因子F对差分进化算法的影响明显大于交叉率CR,F能影响算法的收敛速度。注意到差分进化算法没有跳出局部最优的操作，如果算法收敛太快容易陷入局部最优，而收敛太慢又会影响求解速度。因此我向随机化F来均衡一下算法的收敛速度。
实验7：
F取值为（0,2）内的随机数。
| 参数 | 值 |
| 问题维度(维度) | 2 |
| 小兵数量(种群数) | 20 |
| 进化次数(最大迭代次数) | 50 |
| CR（交叉率） | 0.3 |
| F（放缩因子） | (0,2) |
| 取值范围 | （-100，100） |
| 实验次数 | 10 |
可以看出算法的收敛速度比之前的变慢了一点，再看看结果。
| 参数 | 值 |
| 最优值 | 1.002461804484959E-8 |
| 最差值 | 1.5000010808013516E-4 |
| 平均值 | 2.5148494598068475E-5 |
比之前差。
探究过程中失败是难免的，F为（0,2）内的随机数，那么F的期望为1，其收敛速度变慢导致结果变差也是难免，毕竟最大迭代次数只有50，而且适应度函数过于简单。
方案3：为差分进化算法新增跳出局部最优的操作。
这个方案没有试验，差分进化算法是否需要该操作还是未知数？差分进化算法有着优秀的搜索能力，那么跳出局部最优能力是否需要呢？一个攻击能力超强的战士是否需要加强防御能力呢？
其实我认为还是必要的，因为现在我们需要用优化算法去解决的实际问题大多是动态的而不是实验中的静态还是，在处理动态问题时，一点跳出局部最优能力能够让优化算法快速做出反应而不是再缓慢的进化。只是如何给差分进化算法优雅的添加跳出局部最优性能的方案还没有想到。
5. 总结
差分进化算法的学习在此也告一段落。差分进化算法很强大，也很简单、简洁，算法的描述都充满了美感，不愧是大魔王。不过这里并不是结束，这只是个开始，终将找到打败大魔王的方法，让新的魔王诞生。
由于差分进化算法足够强，而文中实验的问题较为简单导致算法的改进甚至越改越差（其实我也不知道改的如何，需要大量实验验证）。在遥远的将来，也会有更加复杂的问题来检验魔王的能力，总之，后会无期。
