Lattice Planner相关背景和更正式的公式推导可以直接参考其原始论文《Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenét Frame》（ICRA 2010），本文侧重于Lattic planner理论和代码的结合。

1. Lattice Planner基本流程

Lattice Planner算法（含轨迹跟踪算法）的基本流程如下所示：

1. 在笛卡尔坐标系中获取车辆的全局规划路径点（包括起始点和终点）的坐标，如有必要可以按照固定距离重新采样，并进一步计算其角度和曲率的信息；
2. 将上述全局路径作为在Frenet坐标系中进行局部规划的参考线（即坐标轴），转化至Frenet坐标系后获取自车当前在Frenet坐标系下的坐标；
3. 基于上述信息，进行局部轨迹采样，其中构成轨迹需要横纵向解耦，即需要Frenet坐标系中横向（$d,\dot{d},\ddot{d}$等，也可以用符号$l$表示横向），纵向（$s,\dot{s},\ddot{s}$等）和时间尺度（$t$）的信息。横向上基于状态空间（即离散化采点两倍最大道路宽度），局部轨迹的预测时间（例如后续2s-3s的轨迹并进行离散化采点）进行采样，纵向上基于速度和时间序列进行采样，并根据区间起始点终止点的边界条件分别构造横向（五次多项式）和纵向（四次多项式）轨迹；
4. 将上述轨迹重新转化为笛卡尔坐标系，并重新计算角度和曲率等信息，利用预先设定的损失函数、车辆约束条件（最大速度，最大加速度等）、避障所需障碍物信息筛选出最优的局部轨迹；
5. 控制部分：横向根据LQR控制器进行位姿跟踪，纵向根据PID控制器进行速度跟踪；

2. 重要模块所涉及的相关理论知识

2.1. Frenet与笛卡尔坐标系相互转化

显式转化：利用公式

显示的Frenet与笛卡尔坐标系的相互转化公式推导很复杂，这里可以参考up老王的视频进一步学习（其主要思路是利用向量法进行推导），本文只贴出视频中二者的转换公式结论：

直角坐标系转化为Frenet坐标系

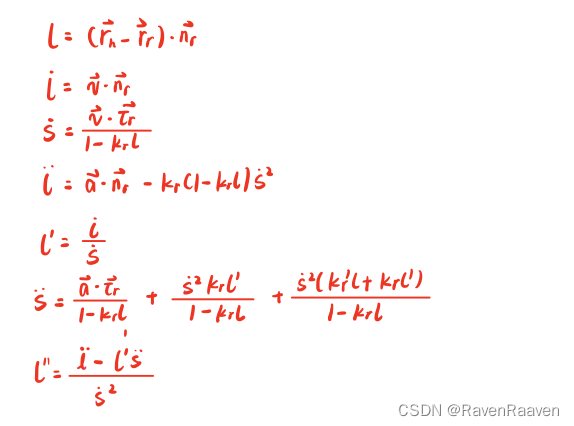
Frenet坐标系转化为直角坐标系（仅包括转化所需要的输入输出）

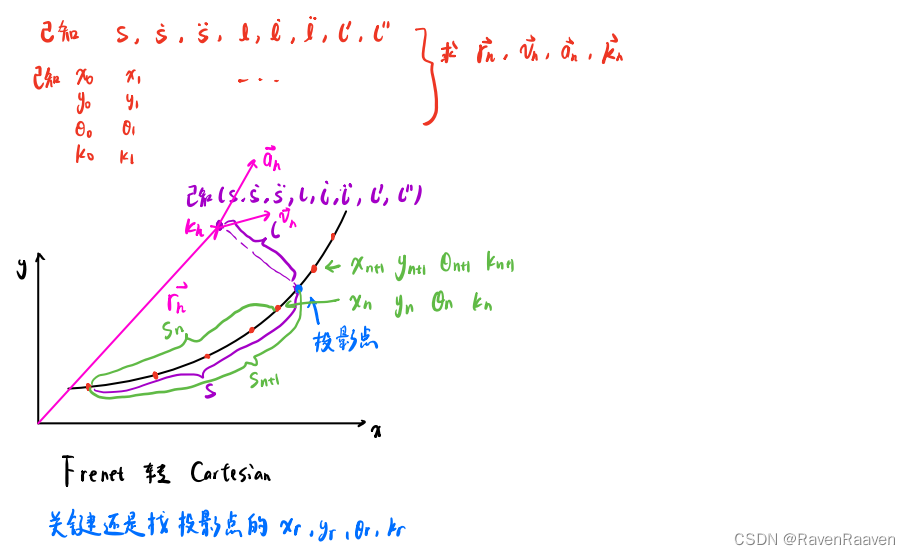
利用三次样条曲线（Cubic Spline）进行隐式求解

本文所介绍的代码实现版本中使用cubic spline进行隐式的坐标转换。本节先对cubic spline中使用natural spline边界条件的方法进行详细推导，内容参考该博客。具体如何实现cubic spline进行Frenet与笛卡尔坐标系的转换见代码实现部分。
用cubic spline进行Frenet到笛卡尔坐标系转化的思路是：分别将笛卡尔坐标系中的$x,y$坐标信息当作为关于Frenet坐标系中$s$（即每个坐标对应的行驶距离）的函数，即$x=f(s),y=g(s)$，$f(\cdot ),g(\cdot )$为不同参数下构造出的cubic spline，后续Frenet转化为Cartesian的过程则使用上述函数进行插值求解。上图以笛卡尔坐标系下坐标轴$x$为例，展示了该方向的离散点。离散化后的自变量区间为$[(s_0,s_1),(s_1,s_2),\dots ,(s_{n-1},s_n)]$，总共$n$个区间，$4n$个参数，$4n$个边界条件。第$i$个区间对应的cubic spline函数记为$S_i(s)$，其本身、一二阶导数公式如下：
$$\{\begin{array}{l}{S}_i(s)=a_i+b_i(s-s_i)+c_i(s-s_i{)}^2+d_i(s-s_i{)}^3\\ S_i^{\prime }(s)=b_i+2c_i(s-s_i)+3d_i(s-s_i{)}^2\\ S_i^{\prime \prime }(s)=2c_i+6d_i(s-s_i)\end{array}$$
所需要的边界条件包括：

1. 所有点满足区间的边界插值点条件，除去端点中间$n-1$个点对应$2(n-1)$个条件，加上2个端点总共$2n$个条件，公式为：$S_i(s_i)=x_i,(i=0,1,\dots ,n-1)$和$S_i(s_{i+1})=x_{i+1},(i=0,1,\dots ,n-1)$；
2. $n-1$个内部点的一阶导数应该是连续的，即$S_i^{\prime }(s_{i+1})=S_{i+1}^{\prime }(s_{i+1}),(i=0,1,\dots ,n-2)$，总共$n-1$个条件；
3. $n-1$个内部点的二阶导数连续，即$S_i^{\prime \prime }(s_{i+1})=S_{i+1}^{\prime \prime }(s_{i+1}),(i=0,1,\dots ,n-2)$，总共$n-1$个条件；
4. 上述总共是$4n-2$个条件，剩下的2个条件有三种方式，本文采用其中的natural spline方式，即$S_0^{\prime \prime }(s_0)=0,S_{n-1}(s_n)=0$；

将上述边界条件带入cubic spline函数和其导数的公式中，进行求解：

• 对于边界条件1的第一个条件，可得$S_i(s_i)=a_i=x_i$；
• 对于边界条件1的第二个条件，令$h_i=s_{i+1}-s_i$，$S_i(s_{i+1})=a_i+b_i{h}_i+c_i{h}_i^2+d_i{h}_i^3=x_{i+1}$
• 对于上述边界条件2，等式左边为$S_i^{\prime }(s_{i+1})=b_i+2c_i{h}_i+3d_i{h}_i^2$，等式右边的$S_{i+1}^{\prime }(s)=b_i+2c_i(s-s_{i+1})+3d_i(s-s_{i+1}{)}^2$，因此代入$s_{i+1}$可得：$S_{i+1}^{\prime }(s_{i+1})=b_{i+1}$，整个边界条件2构成的公式为：$b_i+2c_i{h}_i+3d_i{h}_i^2=b_{i+1}$；
• 同理，对于边界条件3可得公式：$2c_i+6d_i{h}_i=2c_{i+1}$；
• 根据natural spline的条件可得$c_0=0,c_n=0$；

整理一下上述公式：
$$\{\begin{array}{ll}{a}_i=x_i& (1)\\ b_i{h}_i+c_i{h}_i^2+d_i{h}_i^3=x_{i+1}-x_i& (2)\\ b_i+2c_i{h}_i+3d_i{h}_i^2=b_{i+1}& (3)\\ c_i+3d_i{h}_i=c_{i+1}& (4)\end{array}$$

接下来先将参数$b_i,d_i$转化成与$c_i$相关的公式，先整理上述公式$(4)$的$d_i$，再得到$b_i,c_i$之间的关系，可得：
$$\{\begin{array}{l}{d}_i=\frac{c_{i+1}-c_i}{3h_i}\\ b_i=\frac{x_{i+1}-x_i}{h_i}-c_i{h}_i-\frac{h_i}{3}(c_{i+1}-c_i)\end{array}$$

再将所得公式代入上述公式$(3)$可得：
$$h_i{c}_i+2(h_i+h_{i+1})c_{i+1}+h_{i+1}{c}_{i+2}=3\left(\frac{x_{i+2}-x_{i+1}}{h_{i+1}}-\frac{x_{i+1}-x_i}{h_i}\right),i=0,1,\dots ,n-2$$
此时算上natural spline的条件$c_0=0,c_n=0$可以得到所有$n$个关于$c$的方程：
$$\{\begin{array}{l}{c}_0=0,\\ h_0{c}_0+2(h_0+h_1)c_1+h_1{c}_2=3\left(\frac{x_2-x_1}{h_1}-\frac{x_1-x_0}{h_0}\right),\\ h_1{c}_1+2(h_1+h_2)c_2+h_2{c}_3=3\left(\frac{x_3-x_2}{h_2}-\frac{x_2-x_1}{h_1}\right),\\ \dots \\ h_{n-2}{c}_{n-2}+2(h_{n-2}+h_{n-1})c_{n-1}+h_{n-1}{c}_n=3\left(\frac{x_n-x_{n-1}}{h_{n-1}}-\frac{x_{n-1}-x_{n-2}}{h_{n-2}}\right),\\ c_n=0\end{array}$$
整理成矩阵的形式为：

$$\left[\begin{array}{cccccc}1& 0& 0& & \cdots & 0\\ h_0& 2(h_0+h_1)& h_1& 0& & \\ 0& h_1& 2(h_1+h_2)& h_2& 0& \\ 0& 0& h_2& 2(h_2+h_3)& h_3& ⋮\\ ⋮& & \ddots & \ddots & \ddots & \\ & & & & & \\ 0& \cdots & 0& h_{n-2}& 2(h_{n-2}+h_{n-1})& h_{n-1}\\ 0& 0& 0& \cdots & \cdots & 1\end{array}\right]\cdot \left[\begin{array}{c}{c}_0\\ c_1\\ c_2\\ ⋮\\ c_{n-1}\\ c_n\end{array}\right]=3\left[\begin{array}{c}0\\ \frac{x_2-x_1}{h_1}-\frac{x_1-x_0}{h_0}\\ \frac{x_3-x_2}{h_2}-\frac{x_2-x_1}{h_1}\\ ⋮\\ \frac{x_n-x_{n-1}}{h_{n-1}}-\frac{x_{n-1}-x_{n-2}}{h_{n-2}}\\ 0\end{array}\right]=0$$

因此所有参数都可以由$c_i$推导出：
$$\{\begin{array}{l}{a}_i=x_i\\ b_i=\frac{x_{i+1}-x_i}{h_i}-c_i{h}_i-\frac{h_i}{3}(c_{i+1}-c_i)\\ d_i=\frac{c_{i+1}-c_i}{3h_i}\end{array}$$

2.2 局部轨迹采样（横向与纵向）

2.2.1 横向采样

总体思路：横向采样可以在状态空间或控制空间进行采样，本文介绍在状态空间中，即利用结构化道路的最大宽度，进行横向采样的方法。采样点示意图如下所示：

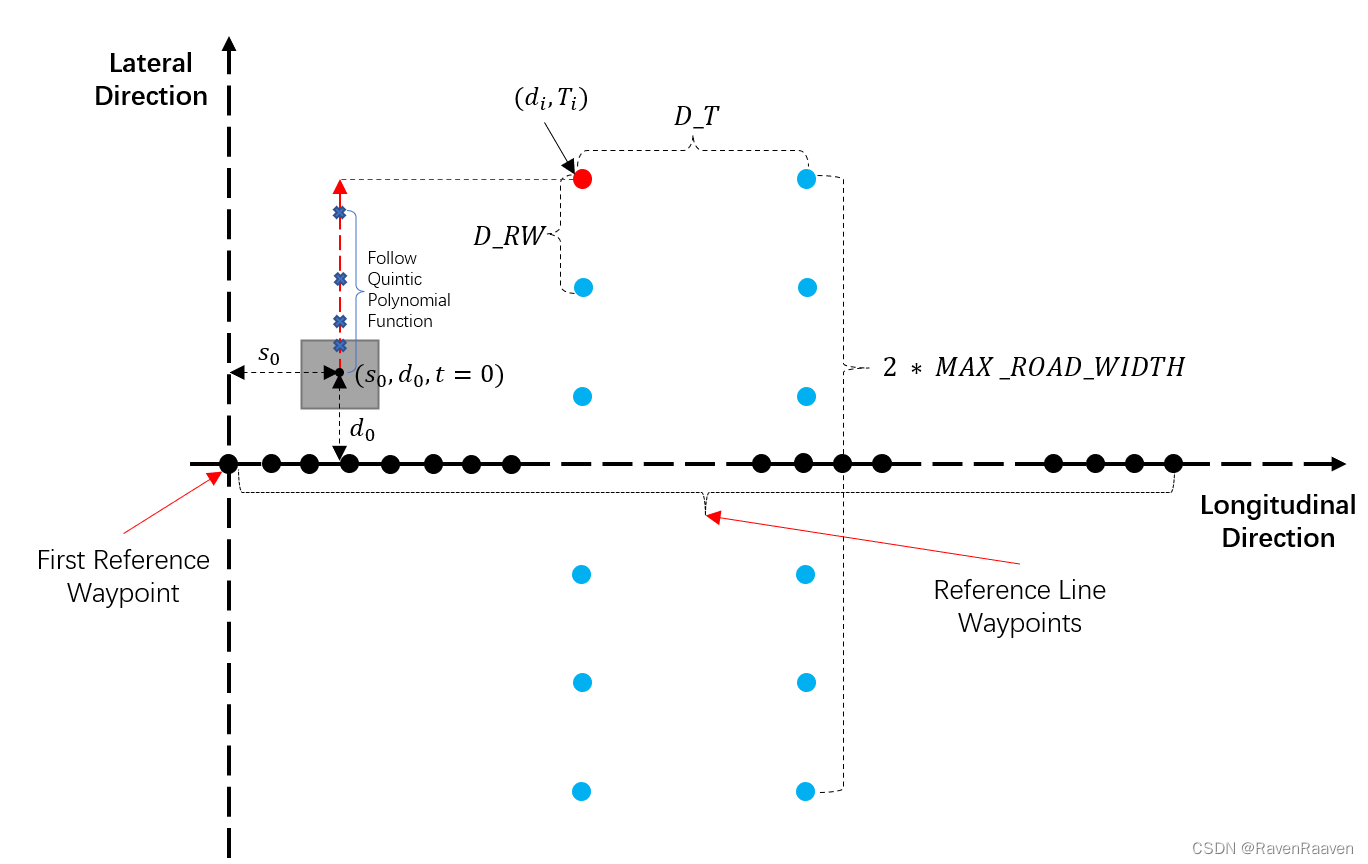
根据已有的采样点，还需要将点与点之间连接起来构成横向轨迹，采用的方法是给定边界条件后根据五次多项式进行连接，五次多项式的公式和一二阶导数公式如下：

$$\{\begin{array}{l}d(t)=a_5{t}^5+a_4{t}^4+a_3{t}^3+a_2{t}^2+a_{1}t+a_0\\ \dot{d}(t)=5a_5{t}^4+4a_4{t}^3+3a_3{t}^2+2a_{2}t+a_1\\ \ddot{d}(t)=20a_5{t}^3+12a_4{t}^2+6a_{3}t+2a_2\end{array}$$

求解五次多项式系数的思路是通过边界条件求解方程中的参数（6个边界条件组成6个方程组以求解6个参数），区间$[0,T_i]$的起始点、终止点边界条件分别有三个，包括位置、速度、加速度条件，分别记为$d(0)=x_s,\dot{d}(0)=v_s,\ddot{d}(0)=a_s$和$d(T_i)=x_e,\dot{d}(T_i)=v_e,\ddot{d}(T_i)=a_e$，整理可得：
$$\{\begin{array}{l}d(0)=x_s=a_0,\\ \dot{d}(0)=v_s=a_1,\\ \ddot{d}(0)=a_s=2a_2\to a_2=\frac{a_s}{2}\\ d(T_i)=a_5{T}_i^5+a_4{T}_i^4+a_3{T}_i^3+a_2{T}_i^2+a_1{T}_i+a_0=x_e,\\ \dot{d}(T_i)=5a_5{T}_i^4+4a_4{T}_i^3+3a_3{T}_i^2+2a_2{T}_i+a_1=v_e,\\ \ddot{d}(T_i)=20a_5{T}_i^3+12a_4{T}_i^2+6a_3{T}_i+2a_2=a_e\end{array}$$

整理成矩阵形式：
$$\left[\begin{array}{ccc}{T}_i^3& T_i^4& T_i^5\\ 3T_i^2& 4T_i^3& 5T_i^4\\ 6T_i& 12T_i^2& 20T_i^3\end{array}\right]\cdot \left[\begin{array}{c}{a}_3\\ a_4\\ a_5\end{array}\right]=\left[\begin{array}{c}{x}_e-a_0-a_1{T}_i-a_2{T}_i^2\\ v_e-a_1-2a_2{T}_i\\ a_e-2a_2\end{array}\right]$$

最终用eigen库求解得到对应的参数即可。

2.2.2 纵向采样

总体思路：纵向采样与横向采样类似，只不过是依据给定的目标速度进行采样，点与点之间的连接方式则采用四次多项式。四次多项式的公式和一二阶导数公式如下：

$$\{\begin{array}{l}s(t)=a_4{t}^4+a_3{t}^3+a_2{t}^2+a_{1}t+a_0\\ \dot{s}(t)=4a_4{t}^3+3a_3{t}^2+2a_{2}t+a_1\\ \ddot{s}(t)=12a_4{t}^2+6a_{3}t+2a_2\end{array}$$

求解四次多项式系数的思路与上述五次多项式相同，用5个边界条件组成的5个方程组以求解5个参数，区间$[0,T_i]$的起始点边界条件分别有三个，包括位置、速度、加速度条件，分别记为$s(0)=x_s,\dot{s}(0)=v_s,\ddot{s}(0)=a_s$，终止点的边界条件只需要两个：$\dot{s}(T_i)=v_e,\ddot{s}(T_i)=a_e$，整理可得：
$$\{\begin{array}{l}s(0)=x_s=a_0,\\ \dot{s}(0)=v_s=a_1,\\ \ddot{s}(0)=a_s=2a_2\to a_2=\frac{a_s}{2}\\ \dot{s}(T_i)=4a_4{T}_i^3+3a_3{T}_i^2+2a_2{T}_i+a_1=v_e,\\ \ddot{s}(T_i)=12a_4{T}_i^2+6a_3{T}_i+2a_2=a_e\end{array}$$

整理成矩阵形式：
$$\left[\begin{array}{cc}3T_i^2& 4T_i^3\\ 6T_i& 12T_i^2\end{array}\right]\cdot \left[\begin{array}{c}{a}_3\\ a_4\end{array}\right]=\left[\begin{array}{c}{v}_e-a_1-2a_2{T}_i\\ a_e-2a_2\end{array}\right]$$

最终用eigen库求解得到对应的参数即可。

2.3 筛选最优局部轨迹

筛选最优局部轨迹依靠最小化损失函数，并判断轨迹是否满足约束条件（车辆的最大速度、最大加速度、最大曲率）与避障条件，其中损失函数构造包括三个部分，代码实现中的损失函数形式为：
$$\{\begin{array}{l}\text{Lateral}:C_d=k_j{J}_t(d(t))+k_{t}T+k_d{d}^2\\ \text{Longitudinal}:C_v=k_j{J}_t(s(t))+k_{t}T+k_d{s}^2\\ \text{Total}:C_f=k_{lat}{C}_d+k_{long}{C}_v\end{array}$$

3. 代码实现

本部分内容主要介绍深蓝学院《自动驾驶控制与规划》课程作业中的代码；首先看一下文件结构：

最重要的文件是frenet_optimal_trajectory.cpp和path_planning_node.cpp，包含了lattice planner算法的核心内容。接下来主要介绍两部分，一是利用cubic spline进行Frenet与笛卡尔坐标系的转化，二是局部轨迹采样的实现。

3.0 代码运行环境配置及目前运行效果

运行环境：Ubuntu 20.04, ROS1, Carla-ROS-bridge, CARLA 0.9.11, C++；
运行指令的顺序：先启动CARLA-ROS-bridge节点，再启动lattice planner；
代码运行截图如下图:

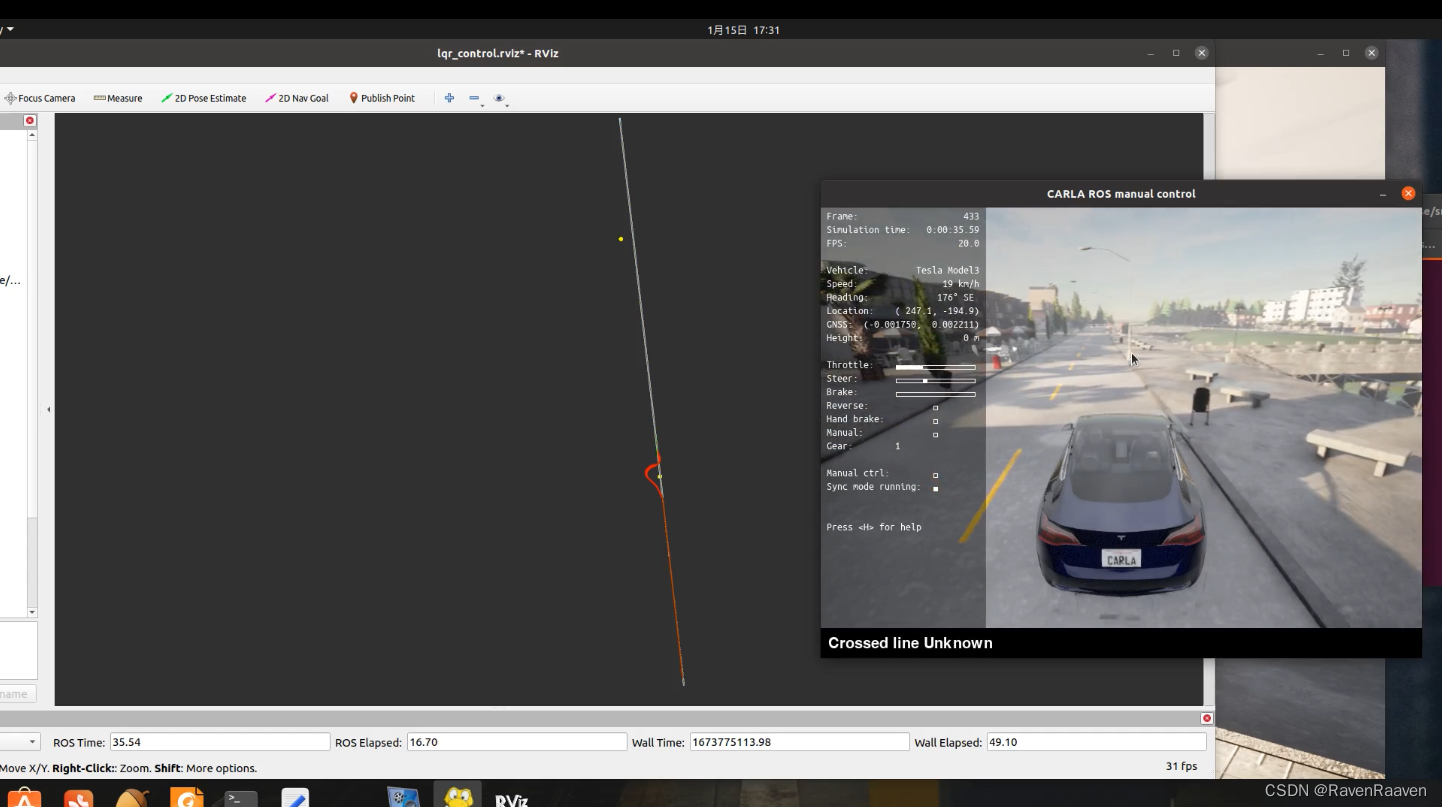
3.1 Cubic Spline实现Frenet到笛卡尔坐标系的转化

转化思路参考第二部分，代码实现部分就是创建一个类，在对象初始化的时候根据矩阵形式用eigen库求解对应的参数，之后若给定随意的自变量，利用二分查找的方式找到该值所在的区间，之后根据cubic spline公式求解即可。

class Spline {
 public:
  Vec_f x;
  Vec_f y;
  int nx;
  Vec_f h;
  Vec_f a;
  Vec_f b;
  Vec_f c;
  // Eigen::VectorXf c;
  Vec_f d;

  Spline(){};
  // d_i * (x-x_i)^3 + c_i * (x-x_i)^2 + b_i * (x-x_i) + a_i
  Spline(Vec_f x_, Vec_f y_)
      : x(x_), y(y_), nx(x_.size()), h(vec_diff(x_)), a(y_) {
    Eigen::MatrixXf A = calc_A();
    Eigen::VectorXf B = calc_B();
    Eigen::VectorXf c_eigen = A.colPivHouseholderQr().solve(B);
    float* c_pointer = c_eigen.data();
    // Eigen::Map<Eigen::VectorXf>(c, c_eigen.rows(), 1) = c_eigen;
    c.assign(c_pointer, c_pointer + c_eigen.rows());

    for (int i = 0; i < nx - 1; i++) {
      d.push_back((c[i + 1] - c[i]) / (3.0 * h[i]));
      b.push_back((a[i + 1] - a[i]) / h[i] -
                  h[i] * (c[i + 1] + 2 * c[i]) / 3.0);
    }
  };

  float calc(float t) {
    if (t < x.front() || t > x.back()) {
      throw std::invalid_argument(
          "received value out of the pre-defined range");
    }
    int seg_id = bisect(t, 0, nx);
    float dx = t - x[seg_id];
    return a[seg_id] + b[seg_id] * dx + c[seg_id] * dx * dx +
           d[seg_id] * dx * dx * dx;
  };

  float calc_d(float t) {
    if (t < x.front() || t > x.back()) {
      throw std::invalid_argument(
          "received value out of the pre-defined range");
    }
    int seg_id = bisect(t, 0, nx - 1);
    float dx = t - x[seg_id];
    return b[seg_id] + 2 * c[seg_id] * dx + 3 * d[seg_id] * dx * dx;
  }

  float calc_dd(float t) {
    if (t < x.front() || t > x.back()) {
      throw std::invalid_argument(
          "received value out of the pre-defined range");
    }
    int seg_id = bisect(t, 0, nx);
    float dx = t - x[seg_id];
    return 2 * c[seg_id] + 6 * d[seg_id] * dx;
  }

 private:
  Eigen::MatrixXf calc_A() {
    Eigen::MatrixXf A = Eigen::MatrixXf::Zero(nx, nx);
    A(0, 0) = 1;
    for (int i = 0; i < nx - 1; i++) {
      if (i != nx - 2) {
        A(i + 1, i + 1) = 2 * (h[i] + h[i + 1]);
      }
      A(i + 1, i) = h[i];
      A(i, i + 1) = h[i];
    }
    A(0, 1) = 0.0;
    A(nx - 1, nx - 2) = 0.0;
    A(nx - 1, nx - 1) = 1.0;
    return A;
  };
  Eigen::VectorXf calc_B() {
    Eigen::VectorXf B = Eigen::VectorXf::Zero(nx);
    for (int i = 0; i < nx - 2; i++) {
      B(i + 1) = 3.0 * (a[i + 2] - a[i + 1]) / h[i + 1] -
                 3.0 * (a[i + 1] - a[i]) / h[i];
    }
    return B;
  };

  int bisect(float t, int start, int end) {
    int mid = (start + end) / 2;
    if (t == x[mid] || end - start <= 1) {
      return mid;
    } else if (t > x[mid]) {
      return bisect(t, mid, end);
    } else {
      return bisect(t, start, mid);
    }
  }
};

二维的spline代码实现如下：

class Spline2D {
 public:
  Spline sx;
  Spline sy;
  Vec_f s;

  Spline2D(Vec_f x, Vec_f y) {
    s = calc_s(x, y);
    sx = Spline(s, x);
    sy = Spline(s, y);
  };

  Poi_f calc_postion(float s_t) {
    float x = sx.calc(s_t);
    float y = sy.calc(s_t);
    return {{x, y}};
  };

  float calc_curvature(float s_t) {
    float dx = sx.calc_d(s_t);
    float ddx = sx.calc_dd(s_t);
    float dy = sy.calc_d(s_t);
    float ddy = sy.calc_dd(s_t);
    return (ddy * dx - ddx * dy) / (dx * dx + dy * dy);
  };

  float calc_yaw(float s_t) {
    float dx = sx.calc_d(s_t);
    float dy = sy.calc_d(s_t);
    return std::atan2(dy, dx);
  };

 private:
  Vec_f calc_s(Vec_f x, Vec_f y) {
    Vec_f ds;
    Vec_f out_s{0};
    Vec_f dx = vec_diff(x);
    Vec_f dy = vec_diff(y);

    for (unsigned int i = 0; i < dx.size(); i++) {
      ds.push_back(std::sqrt(dx[i] * dx[i] + dy[i] * dy[i]));
    }

    Vec_f cum_ds = cum_sum(ds);
    out_s.insert(out_s.end(), cum_ds.begin(), cum_ds.end());
    return out_s;
  };
};

3.2 局部轨迹采样（横向与纵向） 实现

代码实现中的局部轨迹采样如下代码所示：

FrenetPath FrenetOptimalTrajectory::frenet_optimal_planning(
    Spline2D csp, const FrenetInitialConditions& frenet_init_conditions,
    Vec_Poi ob) {
  // 01 获取采样轨迹数组
    Vec_Path fp_list = calc_frenet_paths(c_speed, c_d, c_d_d, c_d_dd, s0);
  // 02 根据参考轨迹与采样的轨迹数组，计算frenet中的其他曲线参数，如航向角，曲率，ds等参数
    calc_global_paths(fp_list, csp);
  // 03 检查路径，通过限制做大速度，最大加速度，最大曲率与避障，选取可使用的轨迹数组
    Vec_Path save_paths = check_paths(fp_list, ob);
    float min_cost = numeric_limits<float>::max();
    FrenetPath final_path;
    for (auto path:save_paths){
      if (path.cf <= min_cost){
          min_cost = path.cf;
          final_path = path;
      }
    }
    return final_path;
}

其中子函数calc_frenet_paths包含了轨迹采样的核心逻辑，其代码由两部分组成，横向和纵向采样，此外，两个方向的采样都需要进行时间轴采样：

Vec_Path FrenetOptimalTrajectory::calc_frenet_paths(float c_speed, float c_d,
                                                    float c_d_d, float c_d_dd,
                                                    float s0) {
  std::vector<FrenetPath> fp_list;

  // 对横向位移 d 进行采样
  for (float di = -1 * MAX_ROAD_WIDTH; di < MAX_ROAD_WIDTH; di += D_ROAD_W) { // sample every 1.0m
    // 对纵向时间序列采样
    for (float Ti = MINT; Ti < MAXT; Ti += DT) { //[2.0, 3.0, 0.2]
      // 当 (di,Ti) 确定后，可获得一条连接当前状态与 (di, Ti) 的五次多项式轨迹曲线
      FrenetPath fp;
      QuinticPolynomial lat_qp(c_d, c_d_d, c_d_dd, di, 0.0, 0.0, Ti);

      // 记录离散时间下对应的轨迹点
      for (float t = 0; t < Ti; t += DT) {
        fp.t.push_back(t);
        fp.d.push_back(lat_qp.calc_point(t));
        fp.d_d.push_back(lat_qp.calc_first_derivative(t));
        fp.d_dd.push_back(lat_qp.calc_second_derivative(t));
        fp.d_ddd.push_back(lat_qp.calc_third_derivative(t));
      }

      // 对纵向车速进行采样
      for (float tv = TARGET_SPEED - D_T_S * N_S_SAMPLE;
           tv < TARGET_SPEED + D_T_S * N_S_SAMPLE; tv += D_T_S) {
        // 当 (vi, Ti) 确定后，可获得一条连接当前状态和 (vi, Ti) 的四次多项式轨迹曲线
        FrenetPath fp_bot = fp;
        QuarticPolynomial lon_qp(s0, c_speed, 0.0, tv, 0.0, Ti);

        // 初始化最大速度和最大加速度
        fp_bot.max_speed = std::numeric_limits<float>::min();
        fp_bot.max_accel = std::numeric_limits<float>::min();
        
        // 记录离散时间下对应的轨迹点
        for (float t_ : fp.t) {
          fp_bot.s.push_back(lon_qp.calc_point(t_));
          fp_bot.s_d.push_back(lon_qp.calc_first_derivative(t_));
          fp_bot.s_dd.push_back(lon_qp.calc_second_derivative(t_));
          fp_bot.s_ddd.push_back(lon_qp.calc_third_derivative(t_));

          // 更新最大加速度和最大速度
          if (fp_bot.s_d.back() > fp_bot.max_speed) {
            fp_bot.max_speed = fp_bot.s_d.back();
          }
          
          if (fp_bot.s_dd.back() > fp_bot.max_accel) {
            fp_bot.max_accel = fp_bot.s_dd.back();
          }
        }

        // 计算代价函数
        float Jp = sum_of_power(fp.d_ddd);      // square of jerk
        float Js = sum_of_power(fp_bot.s_ddd);  // square of jerk
        // square of diff from target speed
        float ds = (TARGET_SPEED - fp_bot.s_d.back());

        fp_bot.cd = KJ * Jp + KT * Ti + KD * std::pow(fp_bot.d.back(), 2);
        fp_bot.cv = KJ * Js + KT * Ti + KD * ds;
        fp_bot.cf = KLAT * fp_bot.cd + KLON * fp_bot.cv;

        // 将轨迹添加至候选轨迹中
        fp_list.push_back(fp_bot);
      }
    }
  }
  return fp_list;
};