目录

一、二叉树 79

1.1树的基本定义79 

1.2数的相关术语 80

1.3二叉树的基本定义 81

1.4二叉查找树的创建 82

1.4.1二叉树查找树创建---插入方法（put） 83

1.4.2二叉树查找树创建---获取方法（get）84

1.4.3二叉树查找树创建---删除方法（delete）85

1.4.4代码的测试 86

1.5二叉查找树其他便捷方法 87

1.5.1查找二叉树中最小的键 87

1.5.2查找二叉树中最大的键 88

1.6二叉树的基础遍历 89

1.6.1二叉树---前序遍历 90

1.6.2二叉树---中序遍历 91

1.6.3二叉树---后序遍历 92

1.7二叉树---层序遍历 93

1.8最大深度问题 94

1.9折纸问题 95

---

一、二叉树 79

1.1树的基本定义79 

数组：

查询的效率比较快，原因是其地址是连续的，根据索引能够快速的查找到。

增删的效率比较慢，每次的增删需要涉及到大量数据的移动。 

链表：

查询的效率比较慢，是因为需要从头结点开始进行查询。  

增删的效率比较快，不需要大量的数据移动，只需要在插入的结点处断开后，然后进行插入即可。

 树：结合了链表和数组的。

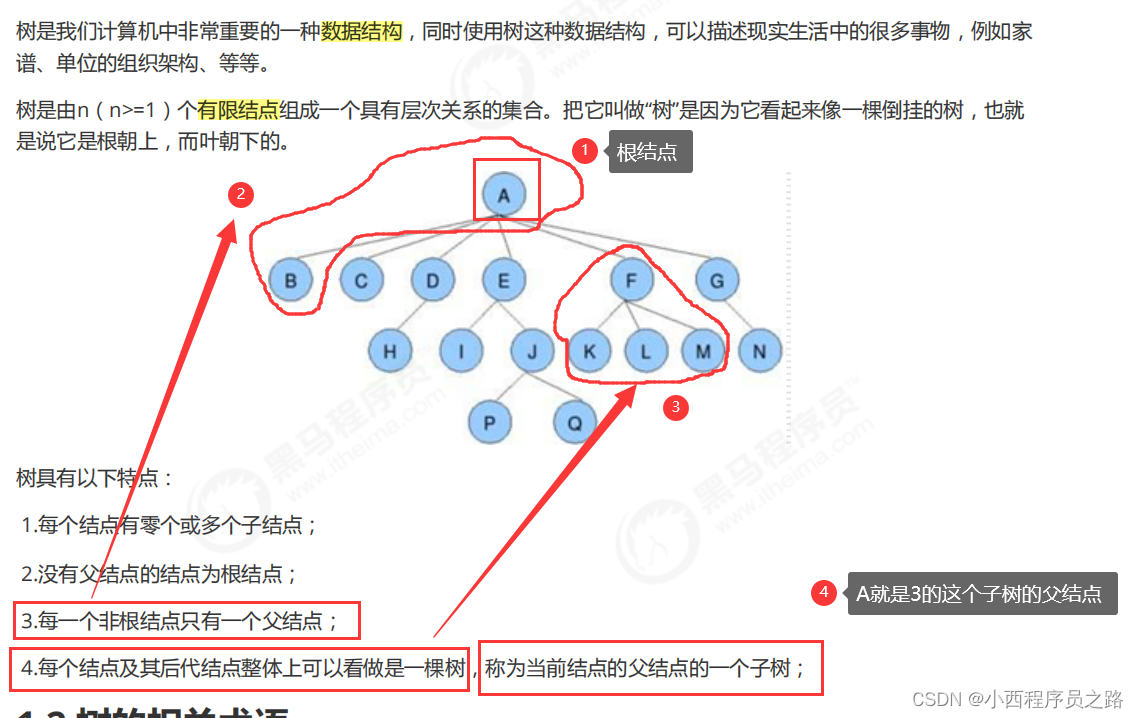
1.2数的相关术语 80

 结点的度： 

叶结点：

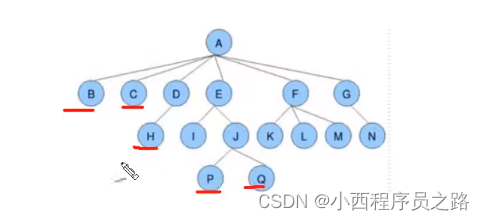
 结点的层序编号：

数的度：

注：根结点的度不一定是最大的

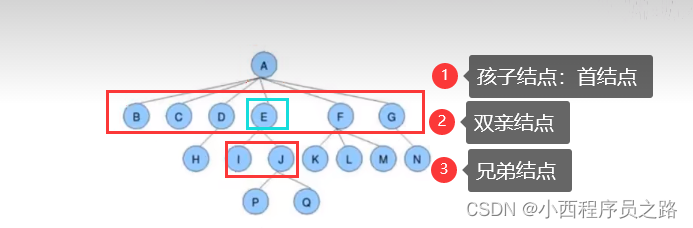
孩子结点、双亲结点、兄弟结点：

1.3二叉树的基本定义 81

二叉树就是度不超过2的数（每个结点最多有两个子结点） 

二叉查找树：左子结点小于右子结点。.

堆：左子结点和右子结点之间没有大小区分。

 

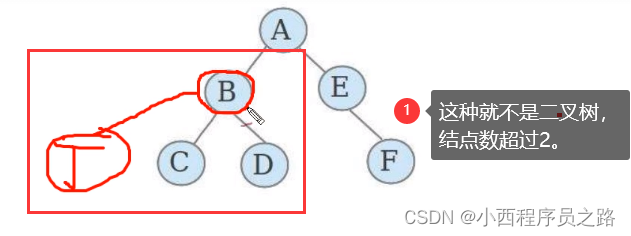
 两个特殊的二叉树：

满二叉树:

 每一层的结点的个数都能达到2^(k-1)  k:层数

完全二叉树：

1.4二叉查找树的创建 82

通过键值对的形式 进行查询。

1.4.1二叉树查找树创建---插入方法（put） 83

插入方法put实现思想：

本部分代码在/tree/BinaryTree中。

1.4.2二叉树查找树创建---获取方法（get）84

查询方法get实现思想：

1.4.3二叉树查找树创建---删除方法（delete）85

删除原来的二叉树之后，需要有一个新的再次替换。这个新的替换是谁比较合适呢？

如何确定这个删除后新替换的元素呢？

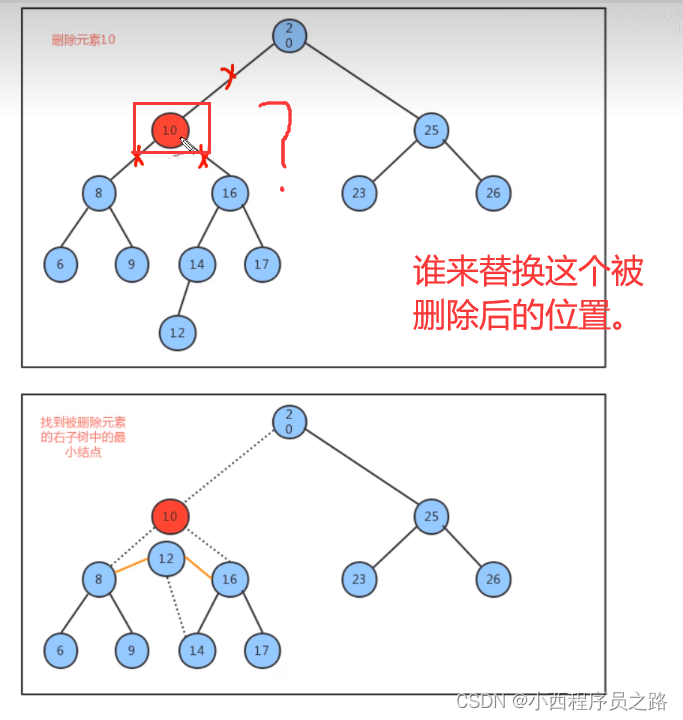
  找到被删除元素的右子树中最小结点，作为替换位置的结点元素。

1.4.4代码的测试 86

本部分代码在/test/BinaryTreeTest中

1.5二叉查找树其他便捷方法 87

1.5.1查找二叉树中最小的键 87

本部分代码在/test/BinaryTree中。最左端的就是最小的键

1.5.2查找二叉树中最大的键 88

本部分代码在/test/BinaryTree中。最右端的就是最大的键

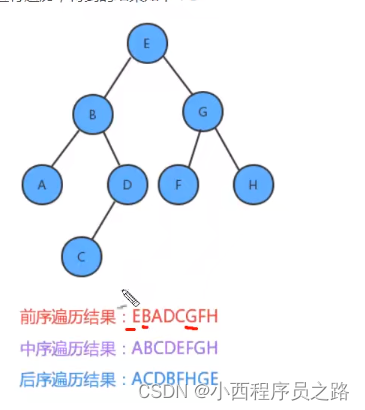
1.6二叉树的基础遍历 89

二叉树的基本遍历的基本的概念： 

遍历方法转换为：搜索路径问题。

搜索路径有三种：（其中最重要的是中序遍历）

示例：

1.6.1二叉树---前序遍历 90

前序遍历代码：/tree/BinaryTree

测试代码：/test/BinaryTreeErgodicTest

1.6.2二叉树---中序遍历 91

中序遍历代码：/tree/BinaryTree

测试代码：/test/BinaryTreeErgodicTest

1.6.3二叉树---后序遍历 92

后序遍历代码：/tree/BinaryTree

测试代码：/test/BinaryTreeErgodicTest

1.7二叉树---层序遍历 93

层序遍历：是从上到下，然后在每层进行从左到右进行查询，进行队列进入。

层序遍历代码：/tree/BinaryTree

测试代码：/test/BinaryTreeErgodicTest

1.8最大深度问题 94

待看 

1.9折纸问题 95

待看