上次讲到我实现了一下代数迭代重建(ART),到周六开会的时候才大概了解了我的研究方向应该是统计迭代重建,一下子就把我给搞懵了。按照书上的说法,统计迭代法是在发射型CT(SPECT和PET)中应用广泛,可我做的是透射型CT啊,还是了解的太少了。加上老师布置了写个Introduction的任务,这周的主要工作就是在各种查资料找文献。但是却始终有种雾里看花的感觉,连自己到底应该往哪个方向走都不知道。今天就是想对这几天看的资料做个总结,试图厘清CT迭代重建算法的发展脉络。任务艰巨,我们都有幸看到这篇推文。

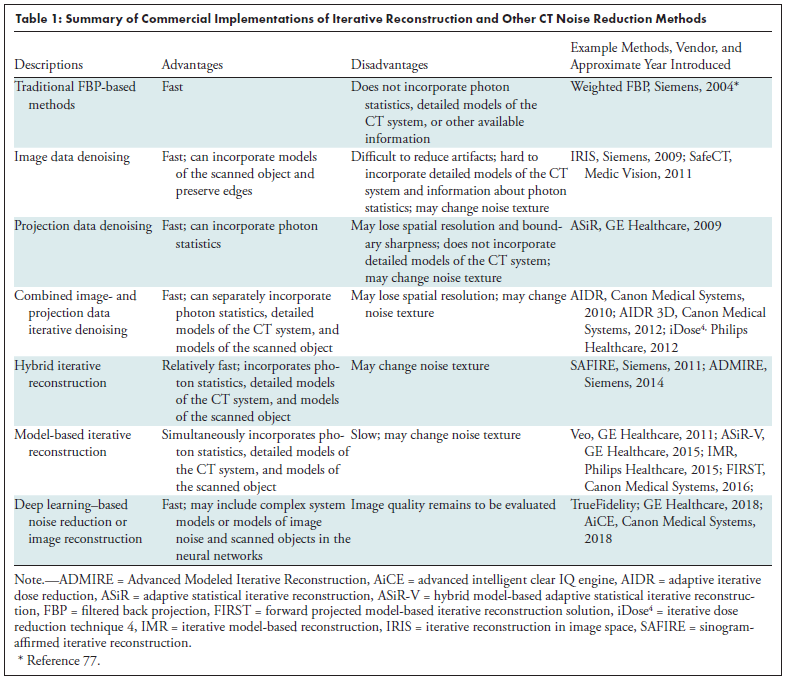
上一次讲到CT的FPB算法及它的各种变种,在早期的商业CT重建算法中,FPB一直占据着霸主地位。关于算法的研究包括对运动的克服,以及在成像过程中修复物理学、仪器、病人和数学方面的不完善等。其实早在70年代,在开发第一代EMI(EMI如果大家不太熟悉的话,它的另一个名字-百代,大家应该听过,就是管理披头士乐队的公司,很难想象两者居然还能有联系。虽然有Hounsfield这样的天才,但是后来EMI在医疗设备的竞争包括创新和营销都比不过西门子、GE和东芝。大部分的创新都是递增的,而不是革命性的,而天才在向前发展中也许并不重要)原型机上,Hounsfield使用的就是一种宽松的迭代重建算法。但是受当时计算机计算能力的限制,无法满足临床应用的需求,于是重建工作转向了FPB。
近年来,由于计算机技术的飞速进步以及CT低剂量的要求,重建算法重新回到研究人员的眼中。迭代重建算法的基本原理是对于某个重建视角,首先在估计的物体图像上通过“前向”投影模拟一个综合投影。这种估计应尽可能地模拟真实CT系统中X射线光子穿过物体并到达探测器的过程。第二步是将综合投影与探测器采集的实际测量值进行比较,误差用于对当前估计得到的图像进行校正。对校正后的图像再次进行迭代,直到误差降为最低得到最终的重建图像。迭代重建算法的优点是:首先,它们允许对X射线源和探测器进行建模,这可以提高重建精度和空间分辨率。其次,光子统计学很容易被考虑,允许算法更多考虑低噪声的投影,降低高噪声的投影,从而减少伪影,提高剂量效率。第三,关于物理物体的一般真实假设,如物体除边缘外倾向于平滑变化,IR算法减少图像噪声,同时保持解剖边界的清晰度。最后,IR算法可以很容易地处理非传统的扫描几何学,例如当数据不是以轴向或螺旋形轨迹获取时。
迭代算法分类
迭代算法大概可以分为四类:

(1) 只在图像空间中迭代(图像修复算法)
如西门子的IRIS(iterativereconstruction in image space),对FPB重建的图像根据噪声模型进行迭代滤波,以降低噪声和伪影。但是具有FPB算法的局限性,包括要求完备的投影数据以及对统计噪声的忽略等。
(2) 只在投影数据空间中迭代(正弦图修复算法)
如GE的ASiR(adaptive statistical iterative reconstruction),对FPB重建的图像做基于统计的、考虑到光子与电子噪声的理想噪声模型校正,再将校正之后的图像正投影后用于更新原始投影数据,如此进行多次迭代计算,获得最终的图像。因为只考虑了噪声模型,而没有结合CT系统细节模型有一定的局限性,可能丧失一部分空间分辨率和边界锐利度。
(3) 在两个空间中迭代(正弦图和图像修复)
如佳能的AIDR(adaptiveiterative dose reduction),可以分别结合光子统计模型,CT系统细节模型和物体模型。
(4) 在两个空间中进行多次正向和反向推算的完全迭代(完全迭代算法)
如GE的Veo,对X射束从焦点到探测器的整个光学采集过程建立多个模型,焦点、X射束、体素和探测器的几何形状等因素均被纳入模型。但是模型复杂,计算量大,重建时间长。
这两天一直纠结于弄清楚我的研究到底属于以上四种的哪一种,好像会有多大的不同一样,也不肯静下心来去多多了解些基础,听了几个师兄师姐的分享,恨不得立马就动手实践,还没学会走呢都想着跑了。写这篇推文的时候又仔细看了看老师给的书,才发现第一遍看的时候遗漏了些东西,又有新收获

投影矩阵
接下来说一下系统矩阵(即正/反投影运算模型)的确定。系统模型对CT迭代图像重建的数值精度和重建图像质量有着重要影响。目前,主流的系统模型主要分为3类:
(1) 像素驱动模型
假设图像像素在像素中心位置,探测器检测到的投影数据值也在探测器的中心位置。正投影:连接光源A与各个像素中心位置B,到达探测器E点,则E点累积B点像素值。把图像中所有像素点对应到探测器上的点,对探测器上的值进行累加则得到投影数据。反投影:已知C、D两点的像素值,插值得到E点像素值,再把E点的值反投影到每个到达E点的像素点上。

这种方法通常用于FBP重建的反投影实现,正投影很少用,因为它会在投影域引入高频伪影。
(2) 射线驱动模型
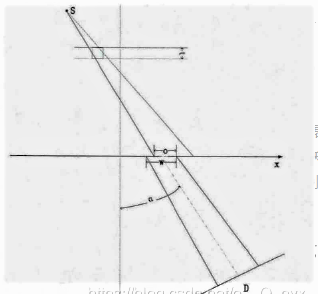
又分为等分点法和交线长度法。等分点法:如图(b)所示,在射线上等间隔采样一系列点,利用最邻近算法或插值算法计算出射线上各点的像素值,累加得到射线对应的投影值。交线长度法:如图(a)所示,计算射线穿过每个网格的长度,乘上该点像素值再进行累加得到投影值。

射线驱动方法在反投影中很少使用,因为它容易在图像域引入高频伪影。为什么这么说呢?因为相邻射线进过的像素信息及投影大小非常接近,导致在反投影的时候会过度偏向某些角度下的信息而忽略其他角度信息。(我猜的)
(3) 距离驱动模型
如图,连接源点和像素的边界中点交X轴于

,连接探测器与源点交X轴于,和分别表示像素值和投影值。


为了正确模拟线积分,将衰减系数除以投影角度的余弦值,并乘以像素尺寸(不懂什么意思,但是下面的具体计算公式可以看懂)。首先将重建图像作一定角度的旋转,使得在几何关系上射线与Y轴的夹角范围始终在[-45,45]内,然后如前面所说将像素边缘和检测器边缘映射到X轴上,那么,某个像素对某个探测器单元的投影贡献值可用下式计算:

其中,其中,S为该检测器单元的投影值,为当前像素单元的灰度值,t为像素纵向尺寸,α为投影角度,o为图像像素映射到X轴与检测器映射到X轴的重叠部分长度,w为检测器单元映射到X轴的长度,如图所示。
它结合了一种高度顺序的存储器访问模式,算法复杂度相对较低,能够既避免了图像域伪影,又避免了投影域伪影,可以用于正投影和反投影过程。
反正我应该是逃不过投影矩阵的计算了,在之前师姐的讲解中没有涉及到这部分,于是我十分执着于想要弄清我们所说的重建是只在图像空间的迭代(后处理)还是其他的。师姐没讲的话应该是目前的研究热点不在这吧。
迭代求解和最优准则
对于投影数据和图像数据,我们可以用下面的方程来表示它们之间的关系:

其中,p为投影数据,R为系统矩阵,x为图像数据,e为误差。那么,从投影重建图像的问题就可以归结为:根据测量矢量p估计图像矢量x。
现在,让我们来回忆一下用有限项级数去逼近一维函数的问题。理论上,我们可以选择任何正交函数集中的基本函数去逼近一维函数,但是我们常用的就是三角函数,于是我们有以下公式:
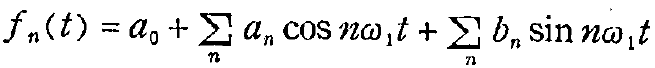
那么,我们只要选取适当的系数,就能足够精确地逼近一维函数。在选取系数的时候应满足某些最优准则,如使误差的均方值最小的准则,于是我们可以用以下公式求解系数:

那么,图像重建的过程也可以分为以上三个步骤:
(1) 选择基本图像
(2) 选择最优准则
(3) 求解相应方程得出合适的最佳图像
下面就讲一下最优准则的选取。在实际过程中,我们会有一个主准则,应选取使得主准则的目标函数最小的图像矢量,如果有一个以上的图像使得目标函数最小,那么我们就有副准则来在其中选择使另一个目标函数最小的一个图像矢量。以下是几个常用的最优准则:
(1) 最小二乘方准则
这一准则使得每一条射线由图像生成的射线和与测量值的误差的平方和最小,其目标函数为:
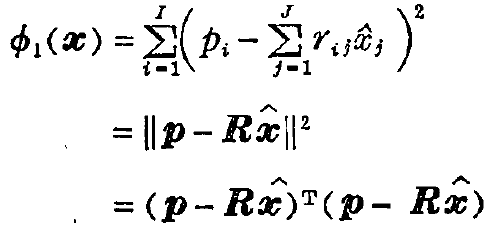
(2) 最大均匀性准则
考虑到一副图像相邻像素间的灰度应该是十分接近的,于是我们有另一个目标函数:

式中,N为不靠边界的像素集合,

为与的3邻域里的其他像素的集合。
(3) 平滑准则
一般说来,一幅图像的灰度变化是比较平缓的,即图像较平滑,所以应使图像的方差最小,于是有第三个目标函数:
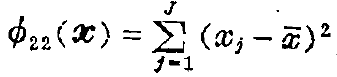
可以看出最大均匀性考虑的是局部的均匀情况,而平滑准则则是整幅图像的均匀度,经过一些推导,我们可以得出一个综合前三个准则的目标函数:
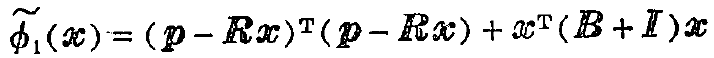

这里B写得有些复杂,其实就是3邻域的拉普拉斯算子乘以它的转置,在边界的时候需要注意补零。
(4) 最大熵准则
设已知图像像素值的平均值为
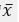
,我们可以有目标函数:

那么像这样的均值为
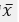
,且使目标函数最大的矢量x最多有一个。在使用的时候,图像均值是根据投影数据进行估计得到的,考虑覆盖图像区域的一组射线投影值的和就可以求得平均像素。最大熵准则特别适用于投影数据不完全场合。
(5) 贝叶斯准则
图像矢量x和测量矢量p可以看作是随机分布中的样本,令

为在所有可能的图像矢量中矢量为x的概率密度;为在给定图像矢量x的情况下,测量矢量为p的概率;为在给定测量矢量p的情况下,图像矢量为x的概率。根据贝叶斯公式,有:

那么,我们要找的x就是使得
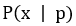
最大的x,称为最大似然x。为了简化,我们假设x和e(误差)都是服从高斯分布的,并且e的期望值为0。通过推导,我们可以得到最大似然x可以通过求解下面的矩阵代数方程得到:

其中,

为x的正定协方差矩阵,为e的协方差矩阵,为x的期望值矢量,I为单位阵。可以证明,最大似然x是使得目标函数取最小值的条件。

其实这个也挺好理解的,本来我们要求一个x使得AX=P,但是本来这个过程中就有噪声的存在,所以我们不可能说使得等式成立。那么,我们就要去寻找最优解,最优解是什么呢?有人认为最小二乘最小的是最优解,有人说这个图像看起来符合期望的是最优解,这就对应了不同的最优化准则的选取。于是,图像重建的过程就成了一个在一定的约束条件下寻找最优解的过程。高数题里大家肯定都碰到过这样的题目,求满足g(x)=0的情况下,f(x)的极值,那会儿也是引入一个,令F(x)=f(x)+g(x),然后求导联立方程组求解。时至今日我才知道这叫拉格朗日乘法。
那么,图像重建的求解过程也可以用同样的方程来表示:

其中,第一项称为保真项,第二项称为惩罚项。于是,在这里面我们看到有几个可以选取的东西:一个是投影矩阵A;一个是||·||范数的选取;一个是正则化参数的选取;一个是惩罚项的选取。不知道该说这里面的东西是大有可为还是说被研究透了。
“匹配的和不匹配的投影运算与反投影运算对”
最后,补充一点曾更生书里的“匹配的和不匹配的投影运算与反投影运算对”。
在离散的情况下,投影运算就是乘以成像矩阵 A 而反投影运算就是乘以转置矩阵 AT。当反投影矩阵是投影矩阵的转置的话,这两个矩阵(或,这两个运算,这两个算子)就称为匹配的。当反投影矩阵不是投影矩阵的转置矩阵的话,这两个矩阵(或,这两个运算,这两个算子)就称为不匹配的。
很显然,在一个迭代算法中,我们不能随便抓一个反投影算子就拿来用。例如,用扇形束的反投影算子来重建平行光束的图像就肯定不行。选择反投影算子的最低要求是先投影再反投影的运算只能让图形变模糊,不能让图形造成畸变,也不能有其它移动(如平移,旋转)。如果一个投影/反投影对施用于一个点源上,其结果只能是在原位置上变得模糊一些而已。


把不匹配的投影/反投影对与匹配的投影/反投影对做个比较,它们对原方程组施加了不同的权函数,进而有不同的噪声效应。它们在采样和数据插值等方面也有不同的性质。这些差别对重建的图像有多大影响,要看具体的成像问题而定。该不该使用不匹配的反投影算子,和使用什么样的反投影算子要具体问题做具体分析。
中间推导我也不想看了,嘿嘿放上来也不是说重要,是我没看它说了个什么,说不定有用呢。
参考文献
1. 研究生熊,
https://mp.weixin.qq.com/s/MzUqRRuOiIzgUg9YUNFQRg [T], 2021.11.12
2. 赵喜同学,
https://mp.weixin.qq.com/s/KBCNq7bUIkxZS8827m2sAw[T], 2020.10.18
3.Wyjun0418,https://blog.csdn.net/qq_37806107/article/details/117323493[C], 2021.05.27
4. 鼎湖影像,
https://www.sohu.com/a/444446383_120051781[S], 2021.01.14
5.Achille M.,LuisS., Cynthia H., et al. Stateof the Art in Abdominal CT: The Limits of Iterative Reconstruction Algorithms.Radiology 2019;293(3):491‐503.
6.董继伟, CT迭代重建技术原理及其研究进展[A], 2016,13(10):128-133.
7.庄天戈, CT算法与重建[M],上海: 上海交通大学出版社,1992.
8.曾更生, 医学图像重建入门[M], 高等教育出版社, 2009.

看了这么多文献,也听了两场学术会议,最大的感受就是CT重建算法一定是和硬件相联系的,CT从第一代的平行光束单个探测器平移加旋转到现在应用最广泛的第三代螺旋CT,以及应用价值不大的第四代环状探测器CT和现在最新的双源CT,重建算法肯定也不一样。说实话,很担心做重建算法会脱离实际应用流于表面,不期望说能实际应用,但是还是要有点价值才好吧。来自小白的担忧。
另外,在查找文献的时候发现学校好多数据库的资源都没有购入,包括基础的知网的一些文献,也不知道是不是我没弄对。另外的话,查文献时也碰到好多问题,没检索到自己想要的(要么就是迭代算法在哪哪的临床应用,要么就是什么什么的研究进展)、不知道哪些文献价值高等,居然死在了第一步上,文献检索的课赶紧开吧,救救孩子。



![[附源码]计算机毕业设计汽车租赁管理系统Springboot程序](https://img-blog.csdnimg.cn/593180309ddb48879f0b66451e62d6d1.png)

![[附源码]JAVA毕业设计社区管理与服务(系统+LW)](https://img-blog.csdnimg.cn/d3a539c9980245a69d4079a34f640b96.png)