文章目录
- 1. 目的
- 2. 使用 `rand()` 的正确姿势
- 3. 使用 TAOCP 公式
- 3.1 实现
- 3.2 使用
- 4. 随机数:用于 Xavier Glorot 初始化
- 4.1 Xavier Glorot 初始化是什么
- 4.2 使用C语言执行 Xavier Glorot 初始化
- 5. References
1. 目的
用于 lenet 网络训练开始时, weight 和 bias 的初始化。
使用C语言,一方面不想用C标准库的 rand(), 希望沿袭 deepdream_c 的风格; 另一方面, rand() 的跨平台性不太够, RAND_MAX 取值和编译器版本相关,有些编译器下无法得到均等概率的均匀分布。考虑用最少的代码, 实现一个精度相当可以的、性能不算太慢的均匀分布的随机数生成器。
2. 使用 rand() 的正确姿势
假设你的目标平台是唯一的,并且觉得 rand() 的参数 min, max 的范围也是确定的, 使得可以得到比较好的均等概率的均匀分布, 那你可以这样实现:
static float get_random(float min, float max)
{
return rand() / ((RAND_MAX + 1U) / (max - min + 1)) + min;
}
3. 使用 TAOCP 公式
代码来自 github, 作者 Bob Adolf. 见参考[2]. ncnn 的单元测试工具, 使用了 prng.h 。这里稍作修改,放在 lenet.c 中:
3.1 实现
//-----------------------------------------------------------------------------------------
// Random Number
//-----------------------------------------------------------------------------------------
// Portable pseudo random number generator by Bob Adolf
// Based on TAOCP, 3.2.2(7), for j=24, k=55, m=2^64
#define LAG1 (UINT16_C(24))
#define LAG2 (UINT16_C(55))
#define RAND_SSIZE ((UINT16_C(1)) << 6)
#define RAND_SMASK (RAND_SSIZE - 1)
#define RAND_EXHAUST_LIMIT LAG2
// 10x is a heuristic, it just needs to be large enough to remove correlation
#define RAND_REFILL_COUNT ((LAG2 * 10) - RAND_EXHAUST_LIMIT)
struct prng_rand_t
{
uint64_t s[RAND_SSIZE]; // Lags
uint_fast16_t i; // Location of the current lag
uint_fast16_t c; // Exhaustion count
};
#define PRNG_RAND_MAX UINT64_MAX
static inline uint64_t prng_rand(struct prng_rand_t* state)
{
uint_fast16_t i;
uint_fast16_t r, new_rands = 0;
if (!state->c)
{ // Randomness exhausted, run forward to refill
new_rands += RAND_REFILL_COUNT + 1;
state->c = RAND_EXHAUST_LIMIT - 1;
}
else
{
new_rands = 1;
state->c--;
}
for (r = 0; r < new_rands; r++)
{
i = state->i;
state->s[i & RAND_SMASK] = state->s[(i + RAND_SSIZE - LAG1) & RAND_SMASK]
+ state->s[(i + RAND_SSIZE - LAG2) & RAND_SMASK];
state->i++;
}
return state->s[i & RAND_SMASK];
}
static inline void prng_srand(uint64_t seed, struct prng_rand_t* state)
{
uint_fast16_t i;
// Naive seed
state->c = RAND_EXHAUST_LIMIT;
state->i = 0;
state->s[0] = seed;
for (i = 1; i < RAND_SSIZE; i++)
{
// Arbitrary magic, mostly to eliminate the effect of low-value seeds.
// Probably could be better, but the run-up obviates any real need to.
state->s[i] = i * (UINT64_C(2147483647)) + seed;
}
// Run forward 10,000 numbers
for (i = 0; i < 10000; i++)
{
prng_rand(state);
}
}
// Clean up our macros
#undef LAG1
#undef LAG2
#undef RAND_SSIZE
#undef RAND_SMASK
#undef RAND_EXHAUST_LIMIT
#undef RAND_REFILL_COUNT
// PRNG_RAND_MAX is exported
static struct prng_rand_t g_prng_rand_state;
#define PRNG_SRAND(seed) prng_srand(seed, &g_prng_rand_state)
#define PRNG_RAND() prng_rand(&g_prng_rand_state)
static float get_random(float a, float b)
{
//return rand() / ((RAND_MAX + 1U) / (max - min + 1)) + min;
float random = ((float)PRNG_RAND()) / (float)(PRNG_RAND_MAX); //RAND_MAX;
float diff = b - a;
float r = random * diff;
return a + r;
}
// End of Random Number
//-----------------------------------------------------------------------------------------
3.2 使用
最简单的用法如下:
void test_random_number()
{
PRNG_SRAND(7767517);
float val = get_random(0.f, 233);
printf("%.6f\n", val);
}
4. 随机数:用于 Xavier Glorot 初始化
4.1 Xavier Glorot 初始化是什么
根据参考[3]知道,如果使用均匀分布初始化,随机数范围是
[
−
x
,
x
]
[-x, x]
[−x,x], 则
x
=
6.0
fan
in
+
fan
out
x = \sqrt{\frac{6.0}{\text{fan}_{\text{in}} + \text{fan}_{\text{out}}}}
x=fanin+fanout6.0
如果用于高斯分布 (均值
μ
=
0
\mu = 0
μ=0),对应的标准差为
x
=
2.0
fan
in
+
fan
out
x = \sqrt{\frac{2.0}{\text{fan}_{\text{in}} + \text{fan}_{\text{out}}}}
x=fanin+fanout2.0
- fan in \text{fan}_{\text{in}} fanin (float) - 当前网络层的输入神经元个数
- fan out \text{fan}_{\text{out}} fanout (float) - 当前网络层的输出神经元个数
4.2 使用C语言执行 Xavier Glorot 初始化
这里只考虑均匀分布的情况, 因为本文使用的 prng.h 的代码是生成均匀分布的随机数。
以 lenet-5 的第一层 C1 卷积层为例, 输入为 32x32 单通道图像, 有6个kernel, 每个 kernel 为 5x5 大小。这里仅考虑第一个 kernel, 用 Xavier Glorot 方式初始化它。
输入数量 fan_in = 1, 输出数量 fan_out = 6。kernel 大小 5x5。对每个 kernel 元素, 赋予同样范围的随机数:
float kernel[5 * 5]; // TODO: initialize
int fan_in = 1;
int fan_out = 6;
float range_abs = m_sqrt(6.0f / (5 * 5 * (fan_in + fan_out)));
for (int i = 0; i < 25; i++)
{
kernel[i] = get_random(-range_abs, range_abs);
}
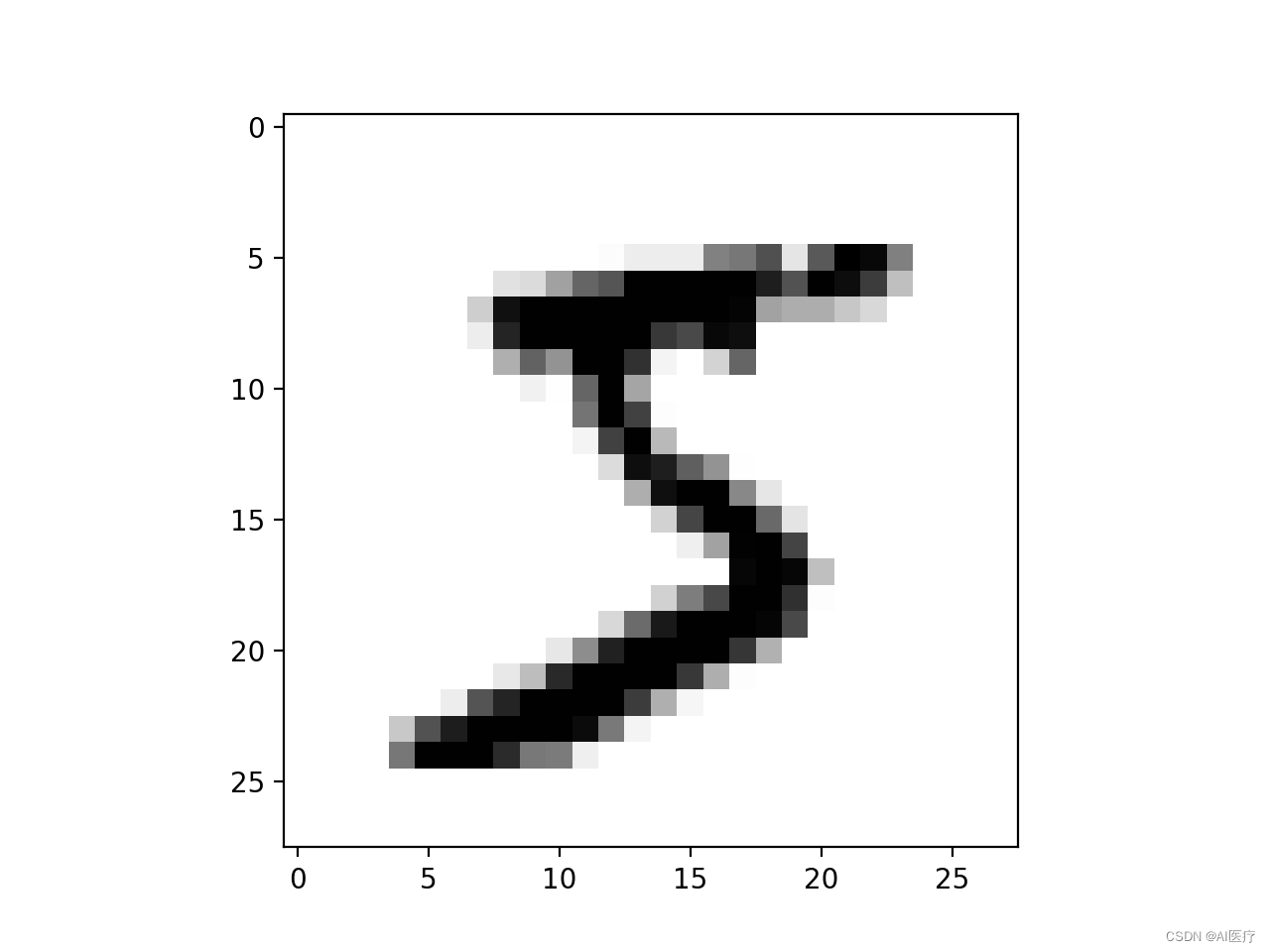
使用该 kernel 做卷积, 输入:

得到的卷积结果(单通道)如下:

5. References
- C/C++随机数用哪个函数?
- <github.com/rdadolf/prng/blob/master/prng.h>
- https://www.bookstack.cn/read/paddlepaddle-1.6/3f4d0d9266a7a5c8.md


![[元带你学: eMMC协议详解 14] 数据擦除(Erase) 详解](https://img-blog.csdnimg.cn/img_convert/262abfa94e2b5642120b21810384ce4b.png)